Construction Of An Angle Using Compass And Ruler
To draw an angle equal to a given angle
In this section, we will learn how to construct angles of 60º, 30º, 90º, 45º and 120º with the help of ruler and compasses only.
Construction Of Some Standard Angles
Construction of an Angle of 60º
In order to construct an angle of 60º with the help of ruler and compasses only, we follow the following steps :
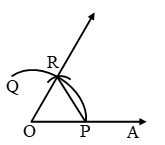
Steps of Construction
Step I: Draw a ray OA.
Step II: With centre O and any radius draw an arc PQ with the help of compasses, cutting the ray OA at P.
Step III: With centre P and the same radius draw an arc cutting the arc PQ at R.
Step IV: Join OR and produce it to obtain ray OB.
The angle ∠AOB so obtained is the angle of measure 60º.
Justification: In above figure, join PR.
In ΔOPR, we have
OP = OR = PR
⇒ ΔOPR is an equilateral triangle.
⇒ ∠POR = 60º
⇒ ∠AOB = 60º [∵ ∠POR = ∠AOB]
(ii) Construction of An Angle of 30º
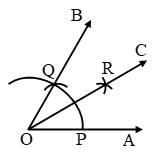
Steps of Construction:
Step I: Draw ∠AOB = 60º by using the steps mentioned above.
Step II: With centre O and any convenient radius draw an arc cutting OA and OB at P and Q respectively.
Step III: With centre P and radius more than \(\frac { 1 }{ 2 } \)(PQ), draw an arc in the interior of ∠AOB.
Step IV: With centre Q and the same radius, as in step III, draw another arc intersecting the arc in step III at R.
Step V: Join OR and product it to any point C.
Step VI: The angle ∠AOC is the angle of measure 30º.
(iii) Construction of An Angle of 90º
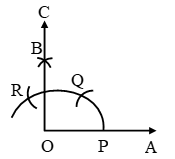
Steps of Construction:
Step I: Draw a ray OA.
Step II: With O as centre and any convenient radius, draw an arc, cutting OA at P.
Step III: With P as centre and the same radius, an arc cutting the arc drawn in step II at Q.
Step IV: With Q as centre and the same radius as in steps II and III, draw an arc, cutting the arc drawn in step II at R.
Step V: With Q as centre and the same radius, draw an arc.
Step VI: With R as centre and the same radius, draw an arc, cutting the arc drawn in step V at B.
Step VII: Draw OB and produce it to C. ∠AOC is the angle of measure 90º.
(iv) Construction of An Angle of 45º
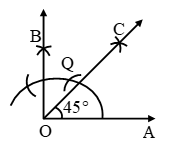
Steps of Construction:
Step I: Draw ∠AOB = 90º by following the steps given above.
Step II: Draw OC, the bisector of ∠AOB.
The angle ∠AOC so obtained is the required angle of measure 45º.
(v) Construction of An Angle of 120º
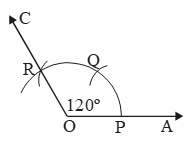
Steps of Construction:
Step I: Draw a ray OA.
Step II: With O as centre and any convenient radius, draw an arc cutting OA at P.
Step III: With P as centre and the same radius draw an arc, cutting the first arc at Q.
Step IV: With Q as centre and the same radius, draw an arc, cutting the arc drawn in step II at R.
Step V: Join OR and produce it to any point C. ∠AOC so obtained is the angle of measure 120º.
Read More:
- Construction of an Equilateral Triangle
- Construction Of Similar Triangle As Per Given Scale Factor
- Construction Of A Line Segment
- Construction Of The Bisector Of A Given Angle
- Construction Of Perpendicular Bisector Of A Line Segment