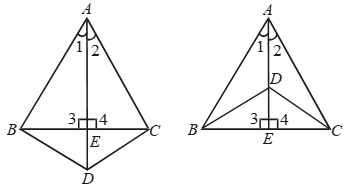
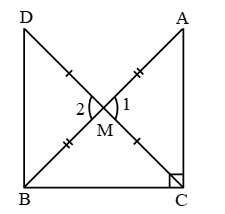
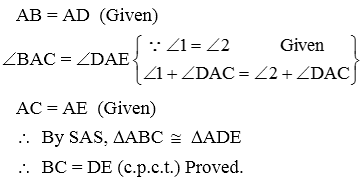How Do You Prove Triangles Are Congruent
https://www.youtube.com/watch?v=GmS-p1S_t5E
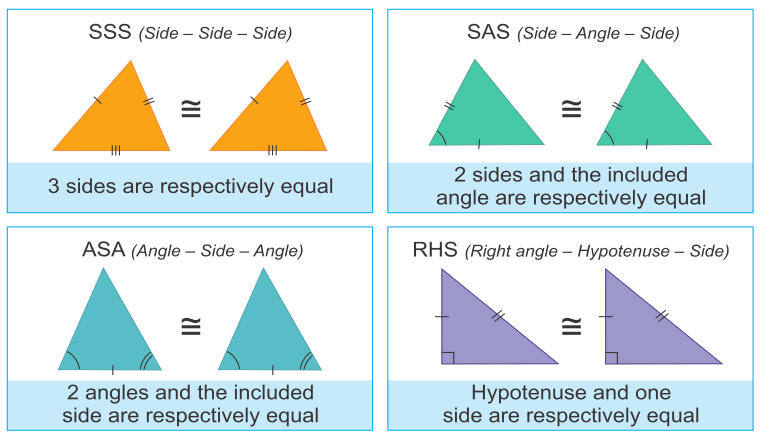
Congruent Figures
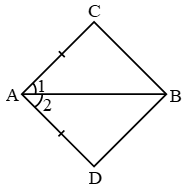
Two figures/objects are said to be congruent if they are exactly of the same shape and size. The relationship between two congruent figures is called congruence. We use the symbol ≅ for ‘congruent to’.
- Congruence among line segments: Two line segments are congruent if they have the same length.
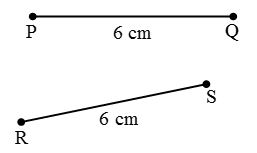
Thus, line segment PQ ≅ line segment RS as PQ = RS = 6 cm. - Congruence of Angles: Two angles are congruent if they have the same measure.
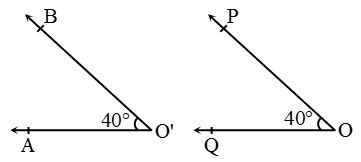
Thus, ∠AO’B ≅ ∠QOP,
as m ∠AO’B = m ∠QOP = 40°. - Congruence of plane figures: Two plane figures A and B are congruent as they superpose each other. We can write it as figure A ≅ figure B.
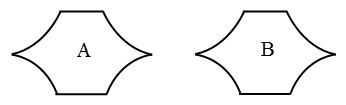
- Congruence of squares: Two squares are congruent if they have same side length.
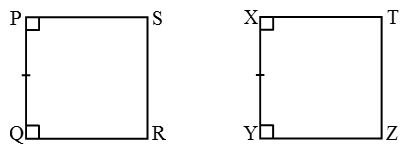
Square PQRS ≅ Square XYZT as PQ = XY. - Congruence of rectangles: Two rectangles are said to be congruent if they have the same length and breadth.
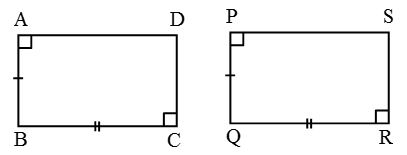
Rectangle ABCD ≅ Rectangle PQRS as
AB = PQ and BC = QR. - Congruence of circles: Two circles are congruent if they have the same radius.
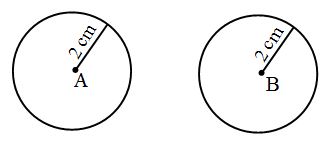
Circle A ≅ Circle B, as radius of A = radius of B = 2 cm.
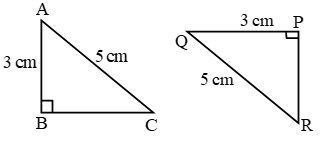
Congruence of Triangles
Two triangles are congruent if they are copies of each other, and when superposed they cover each other exactly.
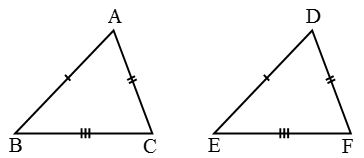 ∆ABC and ∆DEF have the same size and shape. They are congruent. So we would express this as ∆ABC ∆DEF. This means that, when we place ∆DEF on ∆ABC, D falls on A, E falls on B and F falls on C, also \(\overline { DE }\) falls along \(\overline { AB } ,\overline { EF }\) falls along \(\overline { BC }\) and \(\overline { DF }\) falls along \(\overline { AC }\).
∆ABC and ∆DEF have the same size and shape. They are congruent. So we would express this as ∆ABC ∆DEF. This means that, when we place ∆DEF on ∆ABC, D falls on A, E falls on B and F falls on C, also \(\overline { DE }\) falls along \(\overline { AB } ,\overline { EF }\) falls along \(\overline { BC }\) and \(\overline { DF }\) falls along \(\overline { AC }\).
- Corresponding angles are: ∠A and ∠D, ∠B and ∠E, ∠C and ∠F.
- Corresponding vertices are: A and D, B and E, C and F.
- Corresponding sides are: \(\overline { AB }\) and \(\overline { DE } ,\overline { BC }\) and \(\overline { EF } ,\overline { AC }\) and \(\overline { DF }\).
Hence, three sides and three angles are the six matching parts for the congruence of triangles.
Examples:
1. Write the correspondence between the vertices, sides and angles of the triangles XYZ and MLN, if ∆XYZ ≅ ∆MLN.
Solution:
By the order of letters, we find that
X ↔ M, Y ↔ L and Z ↔ N
∴ XY = ML, YZ = LN, XZ = MN
Also ∠X = ∠M, ∠Y = ∠L and ∠Z = ∠N.
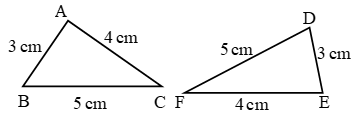
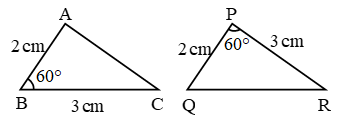
2. In following pairs of triangles, find the correspondence between the triangles so that they are congruent.
In ∆PQR: PQ = 4 cm, QR = 5 cm, PR = 6 cm, ∠P = 60°, ∠Q = 80°, ∠R = 40°.
In ∆XYZ: XY = 6 cm, ZY = 5 cm, XZ = 4 cm, ∠X = 60°, ∠Y = 40°, ∠Z = 80°.
Solution:
Let us draw the triangles and write the measures of their corresponding parts along with them.
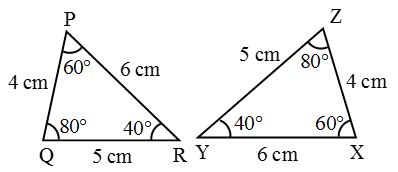
From the above figures, we note that
PQ = XZ, QR = YZ, PR = XY
and ∠P = ∠X, ∠Q = ∠Z, ∠R = ∠Y
∴ P ↔ X, Q ↔ Z and R ↔ Y
Hence, ∆PQR ≅ ∆XZY
Read More:
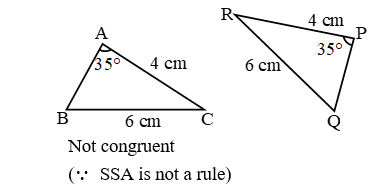
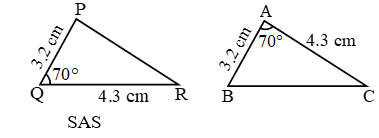
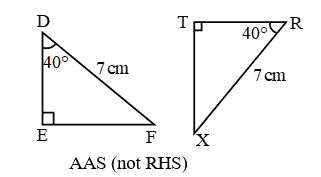
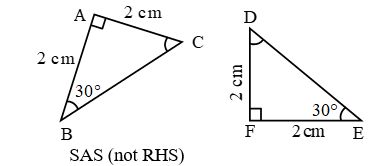
- Criteria For Congruent Triangles
- RS Aggarwal Class 7 Maths Solutions Congruence
- RS Aggarwal Class 9 Solutions Congruence of Triangles and Inequalities in a Triangle
Some more results based on congruent triangles:
- If two sides of a triangle are unequal, then the longer side has the greater angle opposite to it.
- In a triangle, the greater angle has the longer side opposite to it.
- Of all the line segments that can be drawn to a given line, from a point not lying on it, the perpendicular line segment is the shortest.
- The sum of any two sides of a triangle is greater than its third side.
- The difference between any two sides of a triangle is less than its third side.
- Exterior angle is greater than one opposite interior angle.
Congruent Triangles Example Problems With Solutions
Example 1: Find the relation between angles in figure.
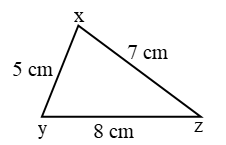
Solution: ∵ yz > xz > xy
⇒∠x > ∠y > ∠z.
(∵ Angle opposite to longer side is greater)
Example 2: Find the relation between the sides of triangle in figure.
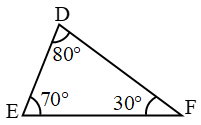
Solution: ∵ ∠D > ∠E > ∠F
∴EF > DF > DE
{∵ side opposite to greater angle is longer}
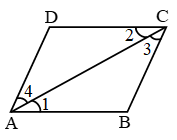
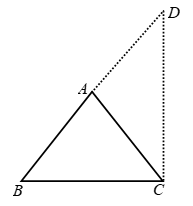
Example 3: Find ∠ACD then what is the relation between (i) ∠ACD, ∠ABC (ii) ∠ACD & ∠A
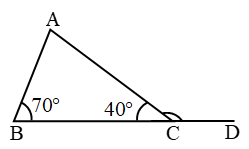
Solution: ∠ACD + 40° = 180° (linear pair)
∠ACD = 140°
also ∠A + ∠B = ∠ACD
(exterior angle = sum of opp. interior angles)
⇒ ∠A + 70° = 140° ⇒ ∠A = 140° – 70°
⇒ ∠A = 70°
Now ∠ACD > ∠B
∠ACD > ∠A
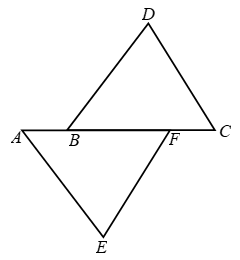
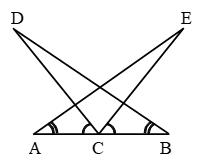
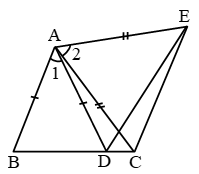
Example 4: In Fig. ∠E > ∠A and ∠C > ∠D. Prove that AD > EC.
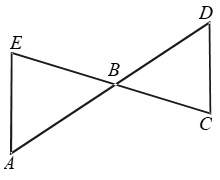
Solution: In ∆ABE, it is given that
∠E > ∠A
⇒ AB > BE …. (i)
In ∆BCD, it is given that
∠C > ∠D
⇒ BD > BC …. (ii)
Adding (i) and (ii), we get
AB + BD > BE + BC ⇒AD > EC
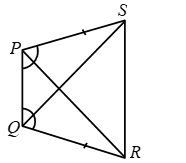
Example 5: AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A > ∠C.
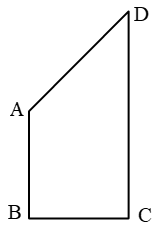
Solution: Draw diagonal AC.
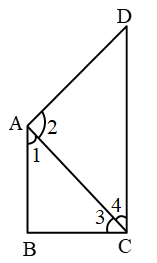
In ∆ABC, AB < BC {∵ AB is smallest}
⇒ ∠3 < ∠1 ……(1)
{angle opp. to longer side is larger}
Also in ∆ADC
AD < CD ∵ CD is longest
⇒ ∠4 < ∠2 …..(2)
adding equation (1) & (2)
∠3 + ∠4 < ∠1 + ∠2
∠C < ∠A
or ∠A > ∠C Proved.
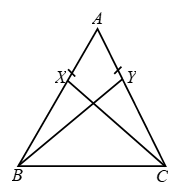
Example 6: In given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.
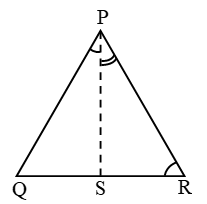
Solution: In ∆PQR, PR > PQ
⇒ ∠Q > ∠R ……(1)
{angle opposite to longer side is greater}
and ∠1 = ∠2 (∵ PS is ∠bisector) ….(2)
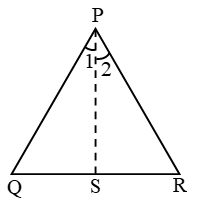
Now for ∆PQS, ∠PSR = ∠Q + ∠1 ….(3)
{exterior angle = sum of opposite interior angle}
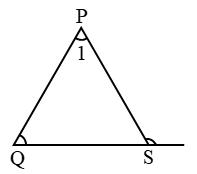
& for ∆PSR, ∠PSQ = ∠R + ∠2 ….(4)
By equation (1), (2), (3), (4), ∠PSR > ∠PSQ
Proved.
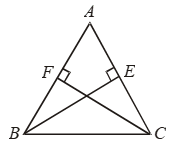
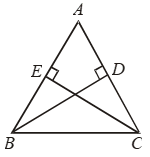
Example 7: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle.
Solution:
In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
ΔBCE ≅ ΔBFC.
⇒ ∠B = ∠C
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ΔABD ≅ ΔABE
⇒ ∠B = ∠A
[∵ Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[∵ Sides opposite to equal angles are equal]
From (i) and (ii), we get
AB = BC = AC
Hence, ΔABC is an equilateral triangle.
Example 8: In Fig. AD = BC and BD = CA.
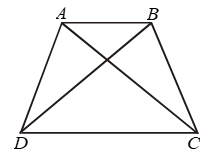
Prove that ∠ADB = ∠BCA and ∠DAB = ∠CBA.
Solution:
In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
ΔABD ≅ ΔCBA ⇒ ∠DAB = ∠ABC
[∵ corresponding parts of congruent triangles are equal]
⇒ ∠DAB = ∠CBA
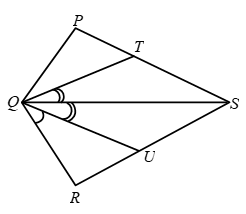
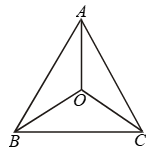
Example 9: In Fig. PQ > PR. QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ > SR.
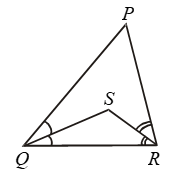
Solution:
In ΔPQR, we have
PQ > PR [Given]
⇒ ∠PRQ > ∠PQR
[∵ Angle opp. to larger side of a triangle is greater]
⇒ \(\frac { 1 }{ 2 } \)∠PRQ > \(\frac { 1 }{ 2 } \)∠PQR
[∵ RS and QS are bisectors of ∠PRQ and ∠PQR respectively]
⇒ ∠SRQ > ∠SQR
⇒ SQ > SR
[∵ Side opp. to greater angle is larger]
Example 10: In Fig.
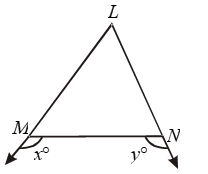
if x > y, show that ∠M > ∠N.
Solution:
We have,
∠LMN + xº = 180º …. (i)
[Angles of a linear pair]
⇒ ∠LNM + yº = 180º …. (ii)
[Angles of a linear pair]
∴ ∠LMN + xº = ∠LNM + yº
But x > y. Therefore,
∠LMN < ∠LNM
⇒ ∠LNM > ∠LMN
⇒ LM > LN
[∵ Side opp. to greater angle is larger]
Example 11: In Fig. AB > AC. Show that AB > AD.
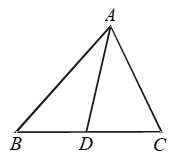
Solution:
In ΔABC, we have
AB > AC [Given]
⇒ ∠ACB > ∠ABC …. (i)
[∵ Angle opp. to larger side is greater]
Now, in ΔACD, CD is produced to B, forming an ext ∠ADB.
⇒ ∠ADB > ∠ACD
[∵ Exterior angle of Δ is greater than each of interior opp. angle]
⇒ ∠ADB > ∠ACB … (ii)
[∴ ∠ACD = ∠ACB]
From (i) and (ii), we get
∠ADB > ∠ABC
⇒ ∠ADB > ∠ABD [∵ ∠ABC = ∠ABD]
⇒ AB > AD
[∵ Side opp. to greater angle is larger]
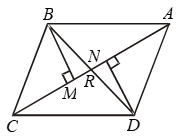
Example 12: Prove that any two sides of a triangle are together greater than twice the median drawn to the third side.
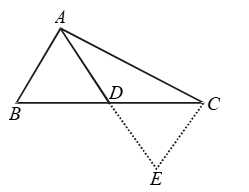
Solution:
To prove: AB + AC > 2 AD
Construction: Produce AD to E such that AD = DE. Join EC.
Proof: In Δ’s ADB and EDC, we have
AD = DE [By construction]
BD = DC [∵ D is the mid point of BC]
and, ∠ADB = ∠EDC [Vertically opp. angles]
So, by SAS criterion of congruence
⇒ ΔADB ≅ ΔEDC
⇒ AB = EC [∵ corresponding parts of congruent triangles are equal]
Now in ΔAEC, we have
AC + EC > AE [∵ Sum of any two sides of a Δ is greater than the third]
⇒ AC + AB > 2 AD
[∵ AD =DE ∴ AE = AD + DE = 2AD and EC = AB]
Example 13: In Fig. PQR is a triangle and S is any point in its interior, show that SQ + SR < PQ + PR.
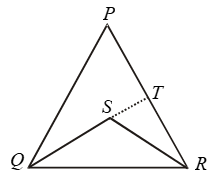
Solution:
Given: S is any point in the interior of ΔPQR.
To Prove: SQ + SR < PQ + PR
Construction: Produce QS to meet PR in T.
Proof: In PQT, we have
PQ + PT > QT [∵ Sum of the two sides of a Δ is greater than the third side]
⇒ PQ + PT > QS + ST …. (i)
[∵ QT = QS + ST]
In ΔRST, we have
ST + TR > SR …. (ii)
Adding (i) and (ii), we get
PQ + PT + ST + TR > SQ + ST + SR
⇒ PQ + (PT + TR) > SQ + SR
⇒ PQ + PR > SQ + SR ⇒ SQ + SR < PQ + PR.
Example 14: In ∆PQR S is any point on the side QR. Show that PQ + QR + RP > 2 PS.
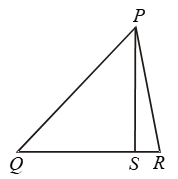
Solution:
In ΔPQS, we have
PQ + QS > PS … (i)
[∵ Sum of the two sides of a Δ is greater than the third side]
Similarly, in ΔPRS, we have
RP + RS > PS …. (ii)
Adding (i) and (ii), we get
(PQ + QS) + (RP + RS) > PS + PS
⇒ PQ + (QS + RS) + RP > 2 PS
⇒ PQ + QR + RP > 2 PS
[∵ QS + RS = QR]
Example 15: In Fig. T is a point on side QR of ∆PQR and S is a point such that RT = ST.
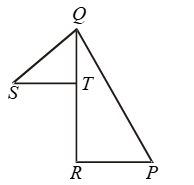
Prove that PQ + PR > QS.
Solution:
In ΔPQR, we have
PQ + PR > QR
⇒ PQ + PR > QT + RT [∵ QR = QT + RT]
⇒ PQ + PR > QT + ST …. (i)
[∵ RT = ST (Given)]
In ΔQST, we have
QT + ST > QS …. (ii)
From (i) and (ii), we get
PQ + PR > QS.
Example 16: Find ∠OBA in given figure
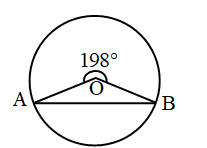
Solution:
∵ ∠AOB + 198° = 360°
∠AOB = 360° – 198° = 162°
and OA = OB = radius of circle
∠A = ∠B = x (let)
∴ x + x + 162° = 180° (a.s.p.)
2x + 18°
x = 9°
∴ ∠OBA = 9°.