Bisector of an angle

What Are The Different Types Of Angles

Angle:
Two rays with a common end point form an angle.
OA, OB are rays & O is end point.

Types of Angles

In geometry, angles can be classified according to the size (or magnitude) of the angle.

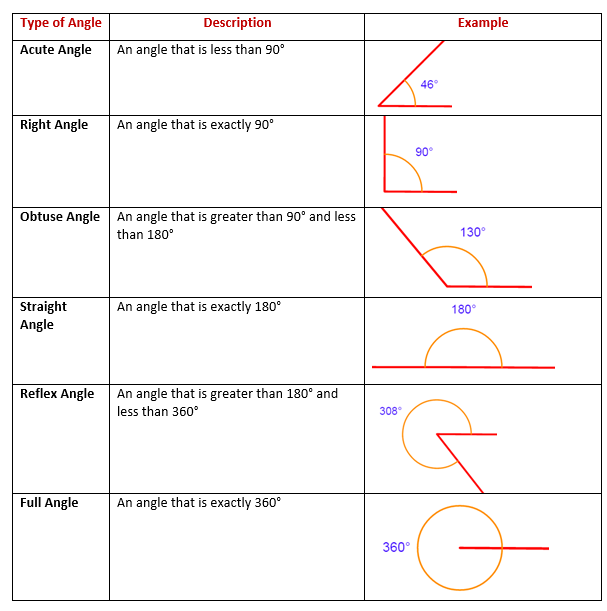
• Right angle: An angle whose measure is 90°, is called a right angle. Two lines that meet at a right angle are said to be perpendicular.
• Acute angle: An angle whose measure is less than 90°, is called an acute angle.
• Obtuse angle: An angle whose measure is greater than 90° and less than 180°, is called an obtuse angle.
• Straight angle: An angle whose measure is 180° is called a straight angle.
• Reflex angle: An angle whose measure is more than 180° but less than 360°, is called a reflex angle.
• Complete angle: An angle whose measure is 360° is called a complete angle.
• Zero angle: An angle whose measure is 0° is called a zero angle.

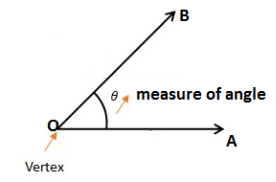
Measure of an angle:
The amount of turning from OA to OB is called the measure of ∠AOB, written as m ∠AOB. An angle is measured in degrees denoted by ‘°’.

• An angle of 360°:
  If a ray OA starting from its original position OA, rotates about O, in the anticlockwise direction and after making a complete revolution it comes back to its original position, we say that it has rotated through 360 degrees, written as 360°.
  
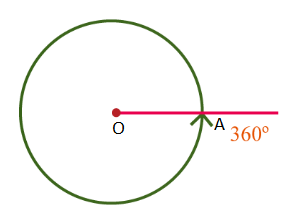
  This complete rotation is divided into 360 equal parts. Each part measures 1°.
  1° = 60 minutes, written as 60′.
  1′ = 60 seconds, written as 60”.
  We use a protractor to measure an angle.
• Bisector of an angle:  
  A ray OC is called the bisector of ∠AOB, if m∠AOC = m∠BOC.
  
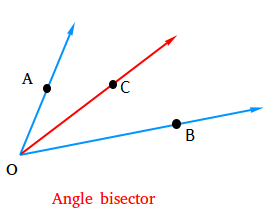
  In this case, ∠AOC = ∠BOC = 1/2 ∠AOB.
• Complementary Angles:
  Two angles are said to be complementary if the sum of their measures is 90°, and each angle is said to be complement of each other.
  For example, (45°, 45°), (10°, 80°), (20°, 70°), (30°, 60°).
  Note:
  (a) If two angles are complement of each other then each angle is an acute angle, but any two acute angles need not be complementary, for example, 20° and 60° are acute angles but are not complement of each other.
  (b) Two obtuse angles and two right angles cannot be complement of each other.
• Supplementary Angles:
  Two angles are said to be supplementary, if the sum of their measures is 180°.
  Two supplementary angles are called the supplement of each other.
  For example, (10°, 170°), (20°, 160°), (30°, 150°), (40°, 140°), (50°, 130°) etc. are all pairs of supplementary angles.
  Note:
  (a) Two acute angles cannot be supplement of each other.
  (b) Two right angles are always supplementary.
  (c) Two obtuse angles cannot be supplement of each other.
• Adjacent Angles:
  Two angles are called adjacent angles, if
  (i) they have the same vertex,
  (ii) they have a common arm and
  (iii) their non-common arms are on either side of the common arm.
  
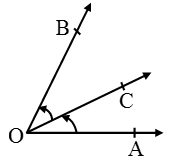
  In the given figure, ∠AOC and ∠BOC are adjacent angles having the same vertex O, a common arm OC and their non-common arms OA and OB on either side of OC.
• Linear Pair Angles
  Two adjacent angles are said to form a linear pair if their non-common arms are two opposite rays.
  In figure, ∠POQ and ∠QOR form a linear pair as their non-common arms OP and OR are two opposite rays i.e., POR is a line.
  
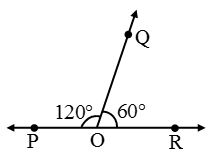
  Note:
  (a) Two linear pair angles can also be adjacent angles but it is not necessary that two adjacent angles will be linear pair angles.
  (b) A pair of supplementary angles forms a linear pair when placed adjacent to each other.
• Vertically Opposite Angles
  Two angles formed by two intersecting lines having no common arm are called vertically opposite angles.
  In figure, two lines PQ and RS are intersecting at point O. We observe that with the intersection of these lines, four angles have been formed.
  
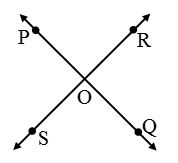
  ∠POR and ∠SOQ form a pair of vertically opposite angles, while ∠POS and ∠ROQ form another pair of vertically opposite angles.
  Note:
  Vertically opposite angles are always equal.
  Important Facts:
  (1) The sum of all angles formed on the same side of a line at a given point on a line is 180°.
  (2) The sum of all angles around a point is 360°.

Types Of Angles Example Problems With Solutions

Example 1:    Find the measure of an angle which is 20° more than its complement.
Soluton:    Let the measure of the required angle be x°.
Then, measure of its complement = (90 – x)°.
∴  x – (90 – x) = 20  ⇔  2x = 110  ⇔  x = 55
Hence, the measure of the required angle is 55°.

Example 2:    Find the measure of an angle which is 40° less than its supplement.
Soluton:    Let the measure of the required angle be x°.
Then, measure of its supplement = (180 – x)°.
∴  (180 – x) – x = 40  ⇔  2x = 140  ⇔  x = 70
Hence, the measure of the required angle is 70°.

Example 3:    Find the measure of an angle, if six times its complement is 12° less than twice its supplement.
Soluton:    Let the measure of the required angle be x°.
Then, measure of its complement = (90 – x)°.
Measure of its supplement = (180 – x)°.
∴  6(90 – x) = 2(180 – x) – 12
⇔  540 – 6x = 360 – 2x – 12
⇔  4x = 192  ⇔  x = 48.
Hence the measure of the required angle is 48°.

Example 4:    Convert 180° in degree, minute & second.
Soluton:    180° = 179° 59′ 60”.

Example 5:    Find the measure of the supplement of an angle of 87°28’43”.
Soluton:    We may write, 180° = 179°59’60”.
∴supplement of an angle of (87°28’43”)
= an angle of [180° – (87°28’43”)]
= an angle of [179°59’60” – 87°28’43”]
= an angle of (92°31’17”).
Hence, the measure of the required angle
= (92°31’17”).

Example 6:    If ∠A = 36°27’46” and ∠B = 28°43’39”,
find ∠A + ∠B.
Soluton:    ∠A + ∠B = 36°27’46” + 28°43’39”
= 64°70’85”
= 64°71’25”
= 65°11’25”

Example 7:    Find the complement of each of the following angles :
(i) 58°       (ii) 16°
(iii) 2/3 of a right angle       (iv) 46° 30′
Soluton:    (i) 90° – 58° = 32°
(ii) 90° – 16° = 74°
(iii) 90° – 2/3 (90°)
= 90° – 60° = 30°
(iv) 90° – 46° 30′
= 89° 60′ – 46° 30′
= 43° 30′

Example 8:    Find the measure of an angle which is complement of itself.
Soluton:    Let the measure of the angle be xº, Then,
Then, the measure of its complement is given to be xº.
Since, the sum of the measures of an angle and its complement is 90º
xº + xº = 90º
⇒ 2xº = 90º
⇒ xº = 45º

Example 9:    Find the measure of an angle which forms a pair of supplementary angles with itself.
Soluton:    Let the measure of the angle be xº. Then,
xº + xº = 180º
⇒ 2xº = 180º
⇒ xº = 90º

Example 10:    An angle is equal to five times its complement. Determine its measure.
Soluton:    Let the measure of the given angle be x degrees. Then, its complement is (90 – x)º.
It is given that :
Angle = 5 × Its complement
⇒ x = 5(90 – x)
⇒ x = 450 – 5x
⇒ 6x = 450
⇒ x = 75
Thus, the measure of the given angles is 75º.

Example 11:    An angle is equal to one-third of its supplement. Find its measure.
Soluton:    Let the measure of the required angle be x degrees. Then,
Its supplement = 180º – x. It is given that:
Angle = 1/3 (Its supplement)
⇒ x = 1/3 (180º – x)
⇒ 3x = 180º – x
⇒ 4x = 180º
⇒ x = 45º
Thus, the measure of the given angle is 45º.

Example 12:    Two supplementary angles are in the ratio 2 : 3. Find the angles.
Soluton:    Let the two angles be 2x and 3x in degrees. Then,
2x + 3x = 180º
⇒ 5x = 180º
⇒ x = 36º
Thus, the two angles are 2x = 2 × 36º = 72º
and 3x = 3 × 36º = 108º

Example 13:    Write the complement of the following angles: 30º 20´
Soluton:    Complement of
30º20′ = 90º – 30º 20′
= 90º – (30º + 20′)
= (89º – 30º) + (1º – 20′)
= 59º + (60′ – 20′)          [∵ 1º = 60′]
= 59º + 40′ = 59º 40′

Example 14:    Find the supplement of the following angles : 134º 30′ 26”
Soluton:    Supplement of an angle of 134º 30′ 26”
= 180º – (134º 30′ 26”)
= (179º – 134º) + (1º – 30′ 26”)
= 45º + (60′ – (30′ + 26”))       [∵ 1º = 60′]
= 45º + (59′ – 30′) + (1′ – 26”)
= 45º + 29′ + 34” = 45º29′ 34”