Selina Concise Mathematics Class 8 ICSE Solutions Chapter 19 Representing 3-D in 2-D
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 19 Representing 3-D in 2-D
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 8 Mathematics Chapter 19 Representing 3-D in 2-D. You can download the Selina Concise Mathematics ICSE Solutions for Class 8 with Free PDF download option. Selina Publishers Concise Mathematics for Class 8 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 8 Maths SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
Representing 3-D in 2-D Exercise 19 – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
If a polyhedron has 8 faces and 8 vertices, find the number of edges in it.
Solution:
Faces = 8
Vertices = 8
using Eulers formula,
F + V – E = 2
8 + 8 – E = 2
-E = 2 – 16
E= 14
Question 2.
If a polyhedron has 10 vertices and 7 faces, find the number of edges in it.
Solution:
Vertices = 10
Faces = 7
Using Eulers formula,
F + V – E = 2
7 + 10 – E = 2
-E = -15
E = 15
Question 3.
State, the number of faces, number of vertices and number of edges of:
(i) a pentagonal pyramid
(ii) a hexagonal prism
Solution:
(i) A pentagonal pyramid
Number of faces = 6
Number of vertices = 6
Number of edges = 10
(ii) A hexagonal prism
Number of faces = 8
Number of vertices = 12
Number of edges = 18
Question 4.
Verily Euler’s formula for the following three dimensional figures:
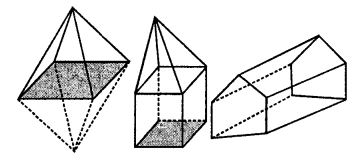
Solution:
(i) Number of vertices = 6
Number of faces = 8
Number of edges = 12
Using Euler formula,
F + V – E = 2
8 + 6 – 12 = 2
2 = 2 Hence proved.
(ii) Number of vertices = 9
Number of faces = 8
Number of edges = 15
Using, Euler’s formula,
F + V – E = 2
9 + 8 – 15 = 2
2 = 2 Hence proved.
(iii) Number of vertices = 9
Number of faces = 5
Number of edges = 12
Using, Euler’s formula,
F + V – E = 2
9 + 5 – 12 = 2
2 = 2 Hence proved.
Question 5.
Can a polyhedron have 8 faces, 26 edges and 16 vertices?
Solution:
Number of faces = 8
Number of vertices = 16
Number of edges = 26
Using Euler’s formula
F + V – E
⇒ 8 + 16 – 26 ≠ -2
⇒ -2 ≠ 2
No, a polyhedron cannot have 8 faces, 26 edges and 16 vertices.
Question 6.
Can a polyhedron have:
(i) 3 triangles only ?
(ii) 4 triangles only ?
(iii) a square and four triangles ?
Solution:
(i) No.
(ii) Yes.
(iii) Yes.
Question 7.
Using Euler’s formula, find the values of x, y, z.

Solution:
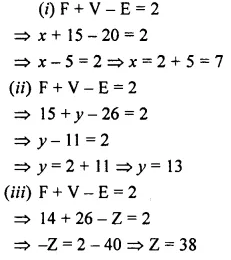
Question 8.
What is the least number of planes that can enclose a solid? What is the name of the solid.
Solution:
The least number of planes that can enclose a solid is 4.
The name of the solid is Tetrahedron.
Question 9.
Is a square prism same as a cube?
Solution:
Yes, a square prism is same as a cube.
Question 10.
A cubical box is 6 cm x 4 cm x 2 cm. Draw two different nets of it.
Solution:
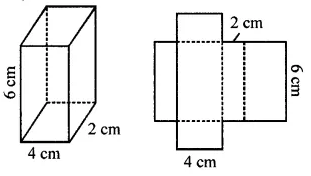
Question 11.
Dice are cubes where the sum of the numbers on the opposite faces is 7. Find the missing numbers a, b and c.
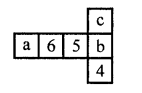
Solution:
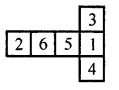
Question 12.
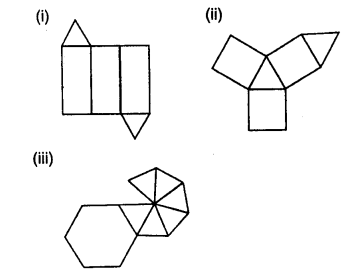
Name the polyhedron that can be made by folding each of the following nets:
Solution:
(i) Triangular prism. It has 3 rectangles and 2 triangles.
(ii) Triangular prism. It has 3 rectangles and 2 triangles.
(iii) Hexagonal pyramid as it has a hexagonal base and 6 triangles.
Question 13.
Draw nets for the following polyhedrons:
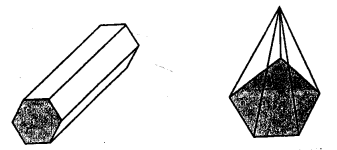
Solution:
Net of hexagonal prism:
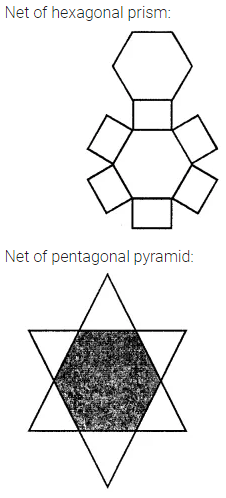
Net of pentagonal pyramid: