Selina Concise Mathematics Class 6 ICSE Solutions Chapter 32 Perimeter and Area of Plane Figures
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 32 Perimeter and Area of Plane Figures
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
IMPORTANT POINTS
1. Perimeter: It is the length of the boundry of the given figure.
(i) Perimeter of a triangle = Sum of its three sides.
(ii) Perimeter of rectangle = 2 (length + breadth)
(iii) Perimeter of square = 4 x side.
2. Area: Area is the measure of surface of the plane covered by a closed plane figure. In other words, we can say that area of a closed plane figure is the measure of its interior region.
(i) Area of rectangle = length x breadth
(ii) Area of square = (side)².
3. Units of measurement of perimeter and area :
(i) Perimeter is measured in centimetre (cm) metre (m) or millimetre (mm).
(ii) Area is measured in square mm, square cm or square metre.
Perimeter and Area of Plane Figures Exercise 32A – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
What do you understand by a plane closed figure?
Solution:
Any geometrical plane figure bounded by lines (straight or curved) in a plane is called a plane closed figure.
Each of the following figures is a plane closed figure.
Question 2.
The interior of a figure is called region of the figure. Is this statement true ?
Solution:
Yes. The interior of the figure alongwith its boundary is called region of the figure
Question 3.
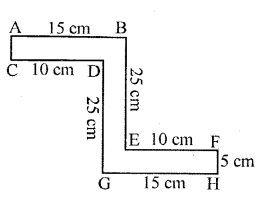
Find the perimeter of each of the following closed figures :
Solution:
(i) Required perimeter
= AB + AC + BE + EF + FH + HG + HD
= 15 + 5 + 25 + 10 + 5 + 15 + 25 = 110 cm
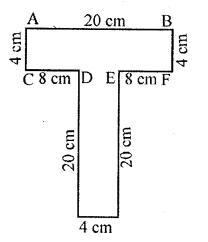
(ii) Required perimeter
= AB + AC + CD + DG + BF + EF + EH + GH
= 20 + 4 + 8 + 20 + 4 + 8 + 20 + 4 = 88 cm
Question 4.
Find the perimeter of a rectangle whose:
(i) length = 40 cm and breadth = 35 cm
(ii) length = 10 m and breadth = 8 m
(iii) length = 8 m and breadth = 80 cm
(iv) length = 3.6 m and breadth = 2.4 m
Solution:
(i) length = 40 cm and breadth = 35 cm
∴Perimeter = 2 (length + breadth)
= 2 (40 cm + 35 cm)
= 2 x 75 cm
= 150 cm = \(\frac { 150 }{ 100 }\)
= 1.5 m
(ii) length = 10 m and breadth = 8 m
∴Perimeter = 2 (length + breadth)
= 2 (10 m + 8 m)
= 2 x 18 m = 54 m
(iii) length = 8 m and
breadth = 80 cm
Length = 8 m
Breadth = 80 cm= \(\frac { 80 }{ 100 }\) m = 0.8 m
∴ Perimeter = 2 (length + breadth)
= 2 (8 m + 0.8m)
= 2 x 8.8 m = 17.6 m
(iv) length = 3.6 m and breadth = 2.4 m
∴ Perimeter = 2 (length + breadth)
= 2 (3.6 m + 2.4 m)
= 2 x 6 m = 12 m
Question 5.
If P denotes perimeter of a rectangle, l denotes its length and b denotes its breadth, find :
(i) l, if P = 38cm and b = 7cm
(ii) b, if P = 3.2m and l = 100 cm
(iii) P, if l = 2 m and b = 75cm
Solution:


Question 6.
Find the perimeter of a square whose each side is 1.6 m.
Solution:
∵ Side of the square = 1.6 m
∴ its perimeter = 4 x side
= 4 x 1.6 m
= 6.4 m
Question 7.
Find the side of the square whose pe-rimeter is 5 m.
Solution:

Question 8.
A square field has each side 70 m whereas a rectangular field has length = 50 m and breadth = 40 m. Which of the two fields has greater perimeter and by how much?
Solution:
Perimeter of the square field = 4 x side = 4 x 70m = 280m
Perimeter of rectangular field = 2 (length + breadth)
= 2 (50 m + 40 m)
= 2 x 90 m
= 180 m
∴Square field has greater perimeter by 280 m – 180 m = 100 m
Question 9.
A rectangular field has length = 160m and breadth = 120 m. Find :
(i) the perimeter of the field.
(ii) the length of fence required to enclose the field.
(iii) the cost of fencing the field at the rate of ? 80 per metre.
Solution:
Given = length = 160 m, breadth = 120m
(i) The Perimeter of the field = 2 (l + b)
= 2 (160 m + 120 m)
= 2 x 280
= 560 m
(ii) The length of fence required to enclose the field = The perimeter of the rectan-gular field
= 560 m
(iii) The cost of fencing the field = Length of fence x Rate of fence
= 560 m x ₹80 per metre
= ₹44, 800
Question 10.
Each side of a square plot of land is 55 m. Find the cost of fencing the plot at the rate of ₹32 per metre.
Solution:
∵Perimeter of square field = 4 x its side = 4 x 55 m
∴Length of required fencing = 220 m Now, the cost of fencing = its length x its rate
= 220 m x ₹32 per metre?
= ₹7040
Question 11.
Each side of a square field is 70 cm. How much distance will a boy walk in order to make ?
(i) one complete round of this field ?
(ii) 8 complete rounds of this field ?
Solution:
(i) Distance covered by the boy to make one complete round of the field.
Perimeter of the field : 4 x its side = 4 x 70 = 280 m
(ii) Distance covered by the boy to make 8 complete rounds of this field.
= 280 m x 8 m = 2240 m
Question 12.
A school playground is rectangular in shape with length = 120 m and breadth = 90 m. Some school boys run along the boundary of the play-ground and make 15 complete rounds in 45 minutes. How much distance they run during this period.
Solution:
Length of the rectangular playground = 120 mBreadth of the rectangular playground = 90 m
∴ Perimeter of the rectangular ground = 2(l + b)
= 2(120 + 90) m = 420 m
Thus, in one complete round, boys covers a distance of = 420 m
∴Distance covered in 15 complete rounds = 420 m x 15 = 6300 m
Question 13.
Mohit makes 8 full rounds of a rect-angular field with length = 120 m and breadth = 75 m.
John makes 10 full rounds of a square field with each side 100 in. Find who covers larger distance and by how much?
Solution:
Mohit
Length of the rectangular field = 120
Breadth of the rectangular field = 75 m
∴ Distance covered in one round (perim-eter) = 2(1 + b)
= 2(120 + 75) = 390 m Hence, distance covered in 8 rounds = 390 x 8 m = 3120 m
John
Side of the field = 100 m
∴Distance covered in one round = 4 x a = 4 x 100 = 400 m
Hence, Distance covered in 10 rounds = 400 x 10 m = 400 m
John a covers greater distance then Mohit by = (4000-3120) m = 880 m
Question 14.
The length of a rectangle is twice of its breadth. If its perimeter is 60 cm, find its length.
Solution:
Let the breadth of the field = x cm
∴ its length = 2x
and, its perimeter = 2 x (length + breadth)
= 2 x (2x + x)
= 2(3x)
= 6x cm
Perimeter = 60 cm
⇒ 60 cm = 6x cm
⇒ x = \(\frac { 60 }{ 6 }\) = 10 cm
∴Breadth = x = 10 cm
Length = 2x = 2 x 10 = 20 cm
Question 15.
Find the perimeter of :
(i) an equilateral triangle of side 9.8 cm.
(ii) an isosceles triangle with each equal side = 13 cm and the third side = 10 cm.
(iii) a regular pentagon of side 8.2 cm.
(iv) a regular hexagon of side 6.5 cm.
Solution:
(i) The perimeter of equilateral triangle = 3 x side
= 3 x 9.8 cm
= 29.4 cm
(ii) Required perimeter = 13 cm + 13 cm + 10 cm
= 36 cm
(iii) Perimeter of given pentagon = 5 x side = 5 x 8.2 cm
= 41 cm
(iv) Perimeter of given hexagon = 6 x side = 6 x 6.5 cm
= 39 cm
Question 16.
An equilateral triangle and d square has equal perimeter. If side of the triangle is 9.6 cm ; what is the length of the side of the square ?
Solution:
Perimeter of equilateral triangle = Perimeter of square Side of triangle = 9.6 cm
∴Perimeter of triangle = 3 x side
= 3 x 9.6 cm = 28.8 cm
> Perimeter of the square = 28.8 cm
4 x the side of square = 28.8 cm
⇒ The side of the square = \(\frac { 28.8 }{ 4 }\) cm
= 7.2 cm Ans.
Question 17.
A rectangle with length = 18 cm and breadth = 12 cm has same perimeter as that of a regular pentagon. Find the side of the pentagon.
Solution:
Length of rectangle = 18 cm
Breadth of rectangle = 12 cm
∴ Perimeter of rectangle = 2 x (l + b)
= 2 x (18+12)
= 2 x 30 = 60 cm
∵Perimeter, of rectangle = Perimeter of pentagon
60 cm = 5 x side
side = \(\frac { 60 }{ 5 }\) cm = 12 cm
∴Side of the pentagon = 12 cm Ans.
Question 18.
A regular pentagon of each side 12 cm has same perimeter as that of a regular hexagon. Find the length of each side of the hexagon.
Solution:
Perimeter of regular pentagon = 5 x length of the side
= 5 x 12 cm = 60 cm
Clearly, perimeter of the given pentagon = 60 cm
⇒ 6 x side of hexagon = 60 cm 60
⇒ side of hexagon = \(\frac { 60 }{ 6 }\)cm = 10 cm
Question 19.
Each side of a square is 45 cm and a rectangle has length 50 cm. If the perimeters of both (square and rectangle) are same, find the breadth of the rectangle.
Solution:

Question 20.
A wire is bent in the form of an equilateral triangle of each side 20 cm. If the same wire is bent in the form of a square, find the side of the square.
Solution:
∵Each side of the given equilateral triangle = 20 cm
∴Perimeter of the triangle = 3 x side = 3 x 20 cm = 60 cm ,
∴ Perimeter of the square = Perimeter of equilateral triangle
⇒ 4 x side of square = 60 cm
⇒ The side of the square = \(\frac { 60 }{ 4 }\)
=15 cm
Perimeter and Area of Plane Figures Exercise 32B – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Find the area of a rectangle whose :
(i) length = 15 cm breadth = 6.4 cm
(ii) Length = 8.5 m breadth = 5 m
(iii) Length = 3.6 m breadth = 90 cm
(iv) Length = 24 cm breadth =180 mm
Solution:

Question 2.
Find the area of a square, whose each side is :
(i) 7.2 cm
(ii) 4.5 m
(iii) 4.1 cm
Solution:
(i) 7.2 cm
Area of the square = (side)² = (7.2 cm)² = 7.2 cm x 7.2 cm = 51.84 cm²
(ii) 4.5 m
Area of the square = (side)² = (4.5 m)² = 4.5 m x 4.5 m = 20.25 m²
(iii) 4.1 cm
Area of the square = (side)² = (4.1 cm)² = 4.1 cm x 4.1 cm = 16.81 cm²
Question 3.
If A denotes area of a rectangle, l represents its length and b represents its breadth, find :
(i) l, if A = 48 cm² and b = 6 cm
(ii) b, if A = 88 m² and l = 8m
Solution:

Question 4.
Each side of a square is 3.6 cm; find its
(i) perimeter
(ii) area.
Solution:
(i) Perimeter = 4 x side
= 4 x 3.6 cm = 14.4 cm
(ii) Area = (side)²
= (3.6 cm)²
= 12.96 cm²
Question 5.
The perimeter of a square is 60 m, find :
(i) its each side its area
(ii) its new area obtained on increasing
(iii) each of its sides by 2 m.
Solution:
Perimeter of a square = 60 m
(i) Perimeter of a square = 4 x side
60 m = 4 x side
\(\frac { 60 }{ 4 }\) = side 4
∴side = 15 m
(ii) Area of square = (side)² = (15 m)²
= 15 m x 15 m
= 225 m²
(iii) Increased each side = 2 m
Side of square = 15 m
New length of side = (2m + 15m)
= 17m
∴New Area of square = (17m)² = 17m x 17m = 289 m²
Question 6.
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Solution:
Each side of square = 7 m
∴Area of square = (side)²= (7 m)²
= 7m x 7m =49m²
∵ Side increased by 3 m
∴Total length of side will be = 3 m + 7 m = 10m
∴Area of square = (10 m)²= 10m x 10 m = 100 m²
∴Increase in area = 100 m² – 49 m² = 51 m²
Question 7.
The perimeter of a square field is numerically equal to its area. Find each side of the square.
Solution:

Question 8.
A rectangular piece of paper has area = 24 cm² and length = 5 cm. Find its perimeter.
Solution:

Question 9.
Find the perimeter of a rectangle whose area = 2600 m² and breadth = 50 m.
Solution:

Question 10.
What will happen to the area of a rectangle, if its length and breadth both are trebled?
Solution:
Let the original length of the rectangle = l and its original breadth = b
∴ its original area = length x breadth i.e A = l – b i. e.
Since,
Increased length -=3l
and, increased breadth = 3b
∴ New area = 3l x 3b = 9 x l x b [∵A = l x b]
⇒ Area of the new rectangle = 9 times than area of original rectangle
Question 11.
Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
Solution:
Length of a rectangle (l) = 30 m,
Breadth of the rectangle (b) = 20 m
Area of rectangle = l x b
= 30 x 20 = 600 m2
Since, the length its increased by 10 m and breadth is doubled
∴New length (l) = (30 + 10) m = 40 m
and new breadth = (20 x 2) m = 40 m
∴New area = l x b = 40 x 40 m2 = 1600 m2
Hence, the increase in the area = (1600 – 600) m2
= 1000 m2
Question 12.
The side of a square field is 16 m. What will be increase in its area, if:
(i) each of its sides is increased by 4 m
(ii) each of its sides is doubled.
Solution:

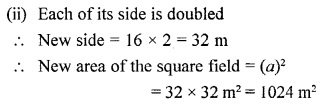
Question 13.
Each rectangular tile is 40 cm long and 30 cm wide. How many tiles will be required to cover the floor of a room with length = 4.8 m and breadth = 2.4 m.
Solution:

Question 14.
Each side of a square tile is 60 cm. How many tiles will be required to cover the floor of a hall with length = 50 m and breadth = 36 m.
Solution:

Question 15.
The perimeter of a square plot = 360 m. Find :
(i) its area.
(ii) cost of fencing its boundary at the rate of ₹ 40 per metre.
(iii) cost of levelling the plot at ₹60 per square metre.
Solution:
Given, perimeter of square plot = 360 m
∵ Perimeter of the square = 4 x its side
∴4 x side of square = 360 m
⇒ side of the square = \(\frac { 360m }{ 4 }\) = 90 m
(i) The area of the square field = (side)²
= (90 m)²
= 90 m x 90 m
= 8100 m²
Cost of fencing at ₹ 40 per metre
= 8100 m2 x ₹ 40 per metre
= ₹ 324000
Cost of levelling at₹ 60 per m²
= 8100 m² x ₹60 per m²
= ₹ 486000
Question 16.
The perimeter of a rectangular field is 500 m and its length = 150 m. Find:
(i) its breadth,
(ii) its area.
(iii) cost of ploughing the field at the rate of ₹1.20 per square metre.
Solution:
(i) Perimeter of a rectangle = 2 x (length + breadth)
⇒500 m = 2x(i50m + breadth)
⇒250 m – 150 m = breadth
∴breadth = 100 m
(ii) Area of rectangular field = length x breadth
= 150 m x 100 m = 15000 m²
(iii) Cost of ploughing the field at the rate of
= ₹1.20 per square m²= area of the field x rate of ploughing = 15000 m² x ₹1.20 per square metre = ₹15000 x 1.20 = ₹18000
Question 17.
The cost of flooring a hall of ₹64 per square metre is ₹2,048. If the breadth of the hall is 5m, find :
(i) its length.
(ii) its perimeter.
(iii) cost of fixing a border of very small width along its boundary at the rate of ₹60 per square metre.
Solution:

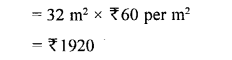
Question 18.
The length of a rectangle is three times its breadth. If the area of the rectangle is 1875 sq. cm, find its perimeter.
Solution:
