ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 1 Rational and Irrational Numbers Chapter Test
Question 1.
Without actual division, find whether the following rational numbers are terminating decimals, or recurring decimals.
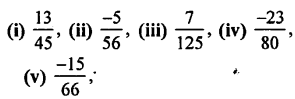
In case of terminating decimals, write their decimal expansions.
Solution:
(i) The fraction whose denominator is the multiple of 2 or 5 or both, Is a terminating decimal.
Now, in \(\frac{13}{45}\), ∵ 45 = 3 × 3 × 5

Question 2.
Express the following recurring decimals as vulgar fractions :
(i) \(1.3 \overline{45}\)
(ii) \(2 . \overline{357}\)
Solution:
(i)Let x= \(1.3 \overline{45}\) = 1.34545 …… (1)
Multiplying both sides of (1) by 10, we get 10x = 13.4545 …..(2)
Multiplying both sides of (2) by 100, we get
1000x = 1345.4545 …….(3)
Subtracting (2) from (3), we get
990x = 1332
⇒ \(x=\frac{1332}{990}=\frac{74}{55}\)
(ii) Let x = \(2 . \overline{357}\) = 2.357357 …….(1)
Multiplying both sides of (1) by 1000, we get.
1000x = 2357.357357 ……..(2)
Subtracting (1) from (2), we get,
999x = 2355 ⇒ x = \(\frac{2355}{999}\)
Question 3.
Insert a rational number between \(\frac{5}{9}\) and \(\frac{7}{13}\), and arrange in ascending order.
Solution:

Question 4.
Insert four rational numbers between \(\frac{4}{5}\) and \(\frac{5}{6}\).
Solution:

Question 5.
Prove that the reciprocal of an irrational number is irrational.
Solution:
Let x be an irrational number
Then its reciprocal will be \(\frac{1}{x}\)
Let \(\frac{1}{x}\) is a non-zero rational number then x × \(\frac{1}{x}\) will be also irrational number as product of a non-zero rational number and irrational numbr is also irrational numbr. But
x × \(\frac{1}{x}\) = 1 which is rational number.
Our supposition is wrong.
∴ \(\frac{1}{x}\) is also an irrational number. x
Hence reciprocal of an irrational number is also an irrational number.
Question 6.
Prove that the following numbers are inrrational.
![]()
Solution:
Suppose \( \sqrt{{8}} \) is a rational number
Let \( \sqrt{{8}} \) = p/q where p and q are integers, q > 0 and p and q have no common factor
squaring both sides
8 = \(\frac{p^{2}}{q^{2}}\)
⇒ p2 = 8 q2
∵ 8q2 is divisible by 8
∴ p22 is also divisible by 8
⇒ p is divisible by 8
Let p = 8k where k is integer.
Squaring both sides,
(p)2 = (8k)2
⇒ p2 = 64k2
∴ 64k2 is divisible by 8
∴ p2 is divisible by 8
⇒ p is divisible by 8
∴ p and q both are divisible by 8
∴ our supposition is wrong
Hence \( \sqrt{{8}} \) is an irrational
(ii) Let \( \sqrt{{14}} \) be a rational number and let \( \sqrt{{14}} \) = \(\frac{p}{q}\) where p and q are integers and q ≠ 0 and
p and q have no common factor,
Squaring both sides,
14= \(\frac{p^{2}}{q^{2}}\) ⇒ p2 = 14q2 …(i)
∴ p2 is divisible by 2
⇒ p is divisible
Let p = 2m
Substituting the value of p in (i)
(2m)2 = 14q2 ⇒ 4m2 = 14q2
⇒ 2m2 = 7q2
∴ q2 is divisible by 2
⇒ q is divisible by 2
⇒ p and q have 2 as the common factor which is not possible
∴ \( \sqrt{{14}} \) is an irrational number
(iii) \(\sqrt[3]{2}\)
suppose \(\sqrt[3]{2}\) is a rational number
Let \(\sqrt[3]{2}\) = p/q where p and q are integers, q > 0, and p and q have no common factor.
cubing both sides,
2 = \(\frac{p^{3}}{q^{3}}\)
⇒ p3 = 2q3
∵ 2q3 is divisible by 2
∴ p3 is divisible by 2
⇒ p is divisible by 2
Let p = 2k where k is an integer
cubing both sides,
(p)3 = (2k)3
⇒ p3 = 8 k3
⇒ 2 q3 = 8k3
⇒ q3 = 4k3
∵ 4k3 is divisible by 2
∴ q3 is divisible by 2
⇒ q is divisible by 2
∴ p and q both are divisible by 2
∴ our supposition is wrong
Hence \(\sqrt[3]{2}\) is an irrational number.
Question 7.
Prove that \( \sqrt{{3}} \) is an irrational number. Hence show that \(5-\sqrt{3}\) is an irrational number.
Solution:
suppose \( \sqrt{{3}} \) is a rational number
Let \( \sqrt{{3}} \) = p/q where p and q are integers, q > 0 and p and q have no common factor Squaring both sides
3 = \(\frac{p^{2}}{q^{2}}\)
⇒ p2 = 3 q2
∵ 3q2 is divisible by 3
∴ p2 is divisible by 3
⇒ p is divisible by 3
Let p = 3k where k is an integer Squaring both sides
p2 = 9k2
∴ 9k2 is divisible by 3
∴ p2 is divisible by 3
⇒ 3q2 a divisible by 3
⇒ q2 is divisible by 3
⇒ q a divisible by 3
∴ p and q both are divisible by 3
∴ Our supposition is wrong .
Hence \( \sqrt{{3}} \) is an irrational number Now in 5 – \( \sqrt{{3}} \), 5 is a rational number and \( \sqrt{{3}} \) is an irrational number (proved)
But difference of a rational number and an irrational number is also an irrational number
∴ (5 – \( \sqrt{{3}} \) ) is an irrational number.
Hence proved.
Question 8.
Prove that the following numbers are irrationals
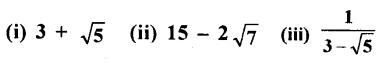
Solution:
(i) Suppose 3 + \( \sqrt{{5}} \) is a rational number say x
Let 3 + \( \sqrt{{5}} \) = x
\( \sqrt{{5}} \) = x – 3
∴ x – 3 is a rational number
∴ \( \sqrt{{5}} \) is also a rational number
Let \( \sqrt{{5}} \) = p/q where p and q are integers, q > 0 and p and q have no common factor squaring both sides
5 = \(\frac{p^{2}}{q^{2}}\)
⇒ p2 = 5 q2
∴ 5q2 is divisible by 5
∴ p2 is divisible by 5
⇒ p is divisible by 5
Let p = 5k, where k is an integer
squaring both sides,
P2 = 25k2
⇒ 5q2 = 25k2
⇒ q2 = 5 k2
5k2 is divisible by 5
∴ q2 is divisible by 5
⇒ q is divisible by 5
∴ p and q both are divisible by 5
∴ our supposition is wrong
∴ \( \sqrt{{5}} \) is an irrational number.
∴ 3 + \( \sqrt{{5}} \) is also an irrational number
Hence prove.
(ii) 15 – 2\( \sqrt{{7}} \)
suppose 15 – 2\( \sqrt{{7}} \) is a rational number say x
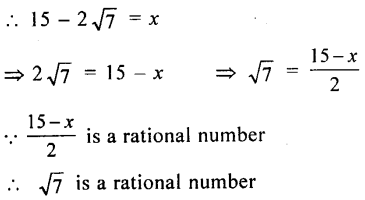
Let \( \sqrt{{7}} \) = p/q where p and q are integers q > 0 and p and q have no common factor Squaring both sides
7 = \(\frac{p^{2}}{q^{2}}\)
⇒ p2 = > 7q2
∵ 7q2 is divisible by 7
⇒ p is divisible by 7
∴ p2 is also divisible by 7
Let p = 7k where k is an integer Squaring both sides
p2 = 49k2
⇒ 7q2 = 49k2
⇒ q2 = 7k2
∵ 7k2 is divisible by 7
∴ q2 is divisible by 7
⇒ q is divisible by 7
∴ p and q both are divisible by 7
∴ our supposition is wrong
Hence \( \sqrt{{7}} \) is an irrational number
15 – 2 \( \sqrt{{7}} \) is also an irrational number
Hence proved.
(iii) \(\frac{1}{3-\sqrt{5}}\)
Rationalising the denominator
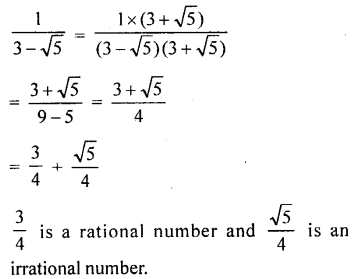
Sum of a rational and an irrational is an irrational number.
Hence proved.
Question 9.
Rationalise the denominator of the following:
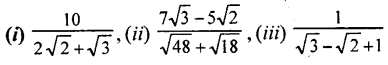
Solution:

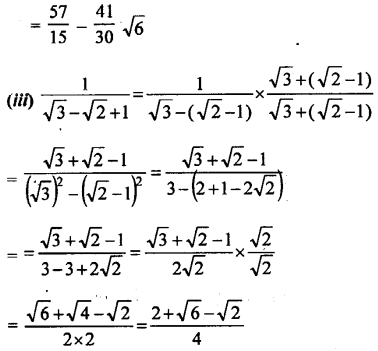
Question 10.
If p, q are rational numbers and \(p-\sqrt{15} q=\frac{2 \sqrt{3}-\sqrt{5}}{4 \sqrt{3}-3 \sqrt{5}}\) find the value of p and q.
Solution:

Question 11.
If x = \(\frac{1}{3+2 \sqrt{2}}\), then find the value of x – \(\frac{1}{x}\).
Solution:
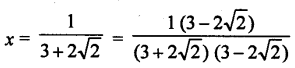
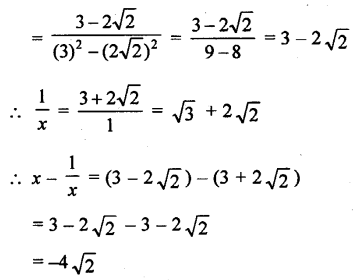
Question 12.
(i) If x = \(\frac{7+3 \sqrt{5}}{7-3 \sqrt{5}}\), find the value of
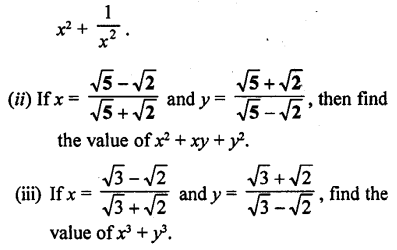
Solution:

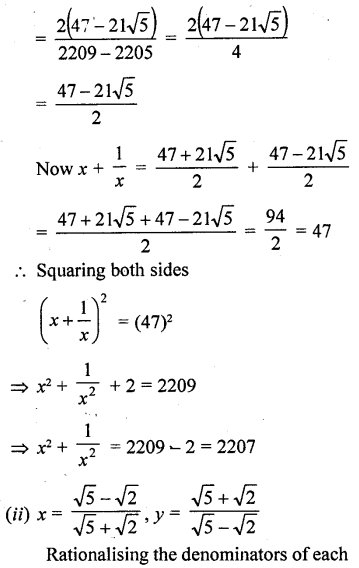
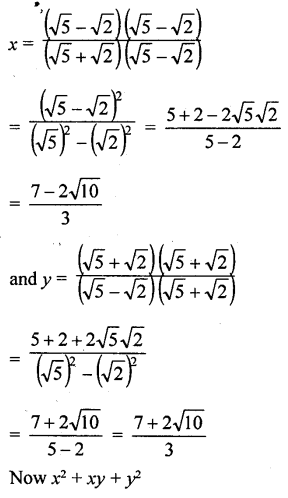
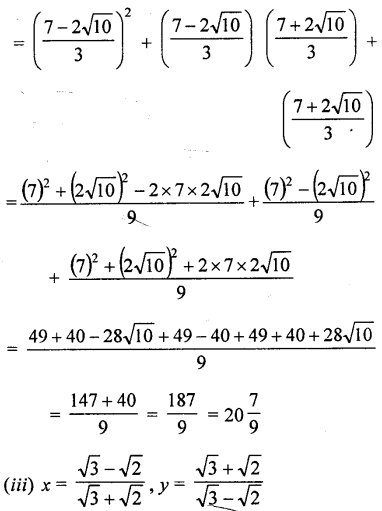


Question 13.
Write the following real numbers in descending order:
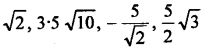
Solution:

Question 14.
Find a rational number and an irrational number between \( \sqrt{{3}} \) and \( \sqrt{{5}} \)?
Solution:
Consider \((\sqrt{3})^{2}\) = 3 and \( \sqrt{{5}} \) = 5
(i) ∵ There is a rational number 4 which is perfect square of a rational number 2
(ii) There can be such more rational numbers which are perfect square.
(iii) One irrational number between \( \sqrt{{3}} \) and \( \sqrt{{5}} \) will be = \(\frac{1}{2}(\sqrt{3}+\sqrt{5})=\frac{\sqrt{3}+\sqrt{5}}{2}\)
Question 15.
Insert three irrational numbers between 2\( \sqrt{{3}} \) and 2\( \sqrt{{5}} \), and arrange in descending order.
Solution:
Consider the square

Question 16.
Give an example each of two different irrational numbers, whose
(i) sum is an irrational number.
(ii) product is an irrational number.
Solution:
(i) Let a = \( \sqrt{{2}} \) b = \( \sqrt{{3}} \)
Which are two irrational number
Also a + b = \( \sqrt{{2}} \) + \( \sqrt{{3}} \) is also irrational number
(ii) Let a = \( \sqrt{{2}} \) b = \( \sqrt{{3}} \)
Which are two irrational number
Also ab = \( \sqrt{{3}} \) \( \sqrt{{3}} \) = \( \sqrt{{6}} \) is also irrational number
Question 17.
Give an example of two different irational numbers, a and b, where \(\frac {a}{b}\) is a rational number.
Solution:
Let a = 3\( \sqrt{{2}} \) and b = 5\( \sqrt{{2}} \) Which are two different irrational numbers,
But, \(\frac{a}{b}=\frac{3 \sqrt{2}}{5 \sqrt{2}}=\frac{3}{5}\) is a rational.
Question 18.
If 34.0356 is expressed in the form \(\frac {p}{q}\) where p and q are coprime integers, then what can you say about the factorisation of q ?
Solution:

which is the form of (2m × 5n) where m and n are positive or non-negative integers.
Question 19.
In each case state whether the following numbers are rational or irrational. If they are rational and expressed in the form \(\frac {p}{q}\). where p and q are coprime integers, then what can you say about the prime factors of q ?
(i) 279.034
(ii) \(76 . \overline{17893}\)
(iii) 3.010010001
(iv) 39.546782
(v) 2.3476817681….
(vi) 59.120120012000
Solution:
(i) 279.034 is a rational number because it has terminating decimals.




(v) 2.3476817681….
It has neither terminating decimals nor repeated
∴ It is an irrational numbers
(vi) 59.120120012000
It has neither terminating decimals nor repeated
∴ It is an irrational number