ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 4 Cubes and Cube Roots Objective Type Questions
Mental Maths
Question 1.
Fill in the blanks:
(i) Cube of an even natural number is …………..
(ii) Cubes of natural numbers are called …………..
(iii) Cube of a natural number whose unit digit is 7, ends with digit …………..
(iv) If a natural number has one zero at its end, then its cube will contain ………….. zero at the end.
(v) Finding cube root is the inverse operation of finding …………..
(vi) If a number can be expressed as the triplets of equal prime factors, then it is called …………..
Solution:
(i) Cube of an even natural number is even number.
(ii) Cubes of natural numbers are called perfect cube.
(iii) Cube of a natural number whose unit digit is 7, pnds with digit 3.
(iv) If a natural number has one zero at its end,
then its cube will contain three zero at the end.
(v) Finding cube root is the inverse operation of finding cube.
(vi) If a number can be expressed as the triplets of equal prime factors,
then it is called perfect cube.
Question 2.
State whether the following statements are true (T) or false (F):
(i) Cube of any odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a single digit number may be asingle digit number.
(vii) If a number is multiplied by 2 then its cube is multiplied by 8.
Solution:
(i) Cube of any odd number is even. False
Correct:
Cube of an odd number is odd.
(ii) A perfect cube does not end with two zeros.
True
(iii) If square of a number ends with 5,
then its cube ends with 25. False
Correct:
Square never ends with only 5, its ends with 25.
(iv) There is no perfect cube which ends with 8.
False
Correct:
Perfect cube can also ends with 8,
for example, the cube of a number whose unit digit is x, will end with 8.
(v) The cube of a two digit number may be a three digit number. False
Correct:
More than three digits.
(vi) The cube of a single digit number may be a single digit number. True
(vii) If a number is multiplied by 2 then its cube is multiplied by 8. True
Multiple Choice Questions
Choose the correct answer from the given four options (3 to 12):
Question 3.
Cube of a negative number is
(a) negative
(b) positive
(c) negative or positive
(d) None of these.
Solution:
The cube of a negative number is negative. (a)
Question 4.
The unit digit of cube of 476 is
(a) 4
(b) 6
(c) 8
(d) 2
Solution:
The unit digit of cube of 476 is 6. (b)
Question 5.
Cube of (-8) is
(a) -512
(b) 512
(c) -64
(d) 64
Solution:
Cube of (-8) is (-512). (a)
Question 6.
Cube of \(\left(\frac{-3}{7}\right)\) is
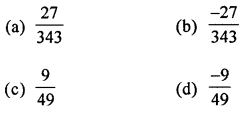
Solution:
Cube of \(\left(\frac{-3}{7}\right) \text { is } \frac{-27}{343}\). (b)
Question 7.
Cube root of -1331 is
(a) 11
(b) 21
(c) -11
(d) -21
Solution:
Cube root of -1331 is -11.
Question 8.
Cube root of 2744 is
(a) 16
(b) 18
(c) -14
(d) 14
Solution:
Cube root of 2744 is 2 × 7 = 14.

Question 9.
Cube root of \(1 \frac{127}{216}\) is
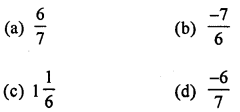
Solution:
Cube root of \(1 \frac{127}{216}\) is
= \(\sqrt{\frac{343}{216}}=\sqrt{\frac{7 \times 7 \times 7}{6 \times 6 \times 6}}=\frac{7}{6}=1 \frac{1}{6}\) (c)
Question 10.
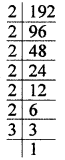
The smallest number by which 192 should be multiplied to make it a perfect cube is
(a) 9
(b) 6
(c) 3
(d) 2
Solution:
The smallest number by which 192
should be multiplied to make it
a perfect cube is 3 × 3 = 9 (a)
Question 11.
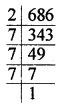
The smallest number by which 686 should be divided to make it a perfect cube is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The smallest number by which 686
should be divided to make it a perfect cube is 2. (b)
Question 12.
The volume of a cube is 729 m3. Length of its side is
(a) 3 m
(b) 6 m
(c) 9 m
(d) 27 m
Solution:
Volume of a cube = 729 m3
∴ Side = \(\sqrt[3]{729}\)
Value Based Question
Question 1.
A school decided to award prizes to their students for three values honesty, punctuality and obedience. If the number of students getting prizes for honesty, punctuality and obedience are in the ratio 1 : 2 : 3 and their product is 162, find the number of students getting prizes for each value.
Which quality you prefer to be rewarded most and why? What values are being promoted?
Solution:
Ratio in three types of awards = 1 : 2 : 3
Product = 162
Let awards be x, 2x, 3x
Then x × 2x × 3x = 162 ⇒ 6x3 = 162
⇒ x3 = \(\frac{162}{6}\) = 27 = (3)3
⇒ x = 3
Number of students of first award = 3 × 1 = 3
Number of students of second award = 3 × 2 = 6
Number of students of third award = 3 × 3 = 9
The awards for honesty, punctuality
and obedience promote the students to be a good citizens.
Higher Order Thinking Skills (Hots)
Question 1.
Find the volume of a cubical box if the cost of painting its outer surface is ₹1440 at the rate of ₹15 per sq. m.
Solution:
Total cost of painting the surface of a cubical box = ₹1440
and rate = ₹15 per sq. m
Total surface = \(\frac{1440}{15}\)= 96 m2
∴ Side = \(\sqrt{\frac{96}{6}}=\sqrt{16}\) = 4m
Now volume = (Side)3 = (4)3 = 64 m32
Question 2.
In a Maths lab there are some cubes and cuboids of the following measurements:
(i) one cube of side 4 cm
(ii) one cube of side 6 cm
(iii) 3 cuboids each of dimensions 4 cm × 4 cm × 6 cm and 3 cuboids each of the dimensions 4 cm × 6 cm × 6 cm.
A student wants to arrange these cubes and cuboids in the form of a big cube. Is it possible for him/her to arrange them in the form of a big cube? If yes, then find the length of side of new cube so formed.
Solution:
(i) One cube of side = 4 cm
∴ Volume = (4)3 = 64 cm3
(ii) One cube of side = 6 cm
Volume = (6)3 = 216 cm3
(iii) 3 cuboids of the size 4 cm × 4 cm × 6 cm
Volume = 4 × 4 × 6 × 3 = 288 cm3
and 3 cuboide of size 4 × 6 × 6 × 3
= 432 cm3
Total volume = 64 + 216 + 288 + 432
= 1000 cm3
∴ Volume of big single cube = 1000 cm3
and side = \(\sqrt[3]{1000}=\sqrt[3]{10 \times 10 \times 10}\) = 10 cm
Yes, possible and side = 10 cm