ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Ex 10.4
Question 1.
Divide:
(i) – 39pq2r5 by – 24p3q3r
(ii) –\(\frac{3}{4}\)a2b3 by \(\frac{6}{7}\)a3b2
Solution:
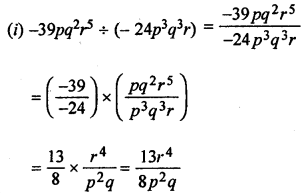
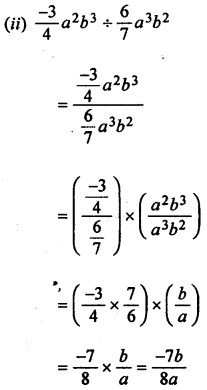
Question 2.
Divide:
(i) 9x4 – 8x3 – 12x + 3 by 3x
(ii) 14p2q3 – 32p3q2 + 15pq2 – 22p + 18q by – 2p2q.
Solution:
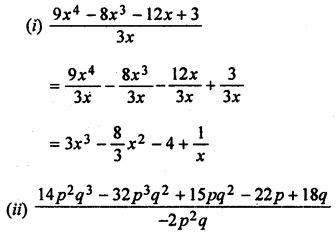
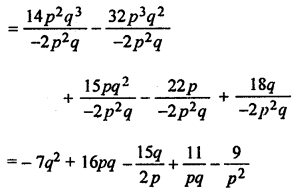
Question 3.
Divide:
(i) 6x2 + 13x + 5 by 2x + 1
(ii) 1 + y3 by 1 + y
(iii) 5 + x – 2x2 by x + 1
(iv) x3 – 6x2 + 12x – 8 by x – 2
Solution:
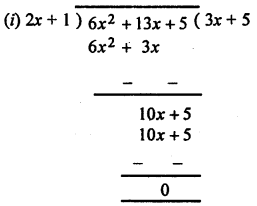
∴ Quotient = 3x + 5
and remainder = 0
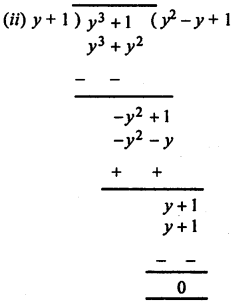
∴ Quotient = y2 – y + 1
and remainder = 0
(iii) Arranging the terms of dividend in descending order
of powers of x and then dividing, we get
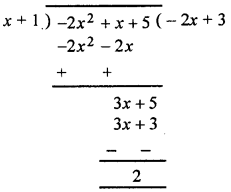
∴ Quotient = – 2x + 3 and remainder = 2
(iv) x3 – 6x2 + 12x – 8 by x – 2
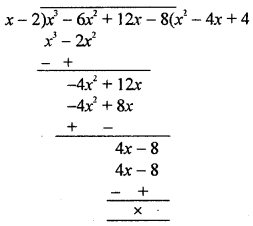
Quotient = x2 – 4x + 4 and remainder = 0
Question 4.
Divide:
(i) 6x3 + x2 – 26x – 25 by 3x – 7
(ii) m3 – 6m2 + 7 by m – 1
Solution:
(i)
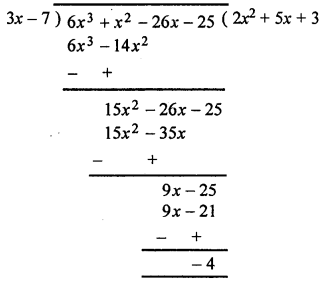
∴ Quotient = 2x2 + 5x + 3 and remainder = – 4
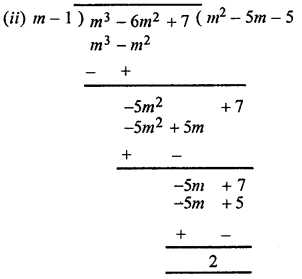
∴ Quotient = m2 – 5m – 5 and remainder = 2.
Question 5.
Divide:
(i) a3 + 2a2 + 2a + 1 by + a2 + a + 1
(ii) 12x3 – 17x2 + 26x – 18 by 3x2 – 2x + 5
Solution:
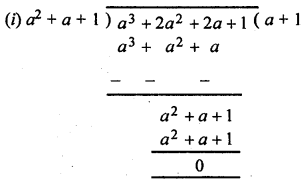
∴ Quotient = a + 1 and remainder = 0.
(ii) 12x3 – 17x2 + 26x – 18 by 3x2 – 2x + 5
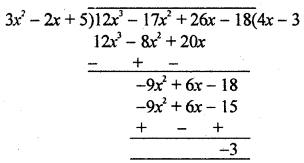
∴ Quotient = 4x – 3 and remainder = -3
Question 6.
If the area of a rectangle is 8x2 – 45y2 + 18xy and one of its sides is 4x + 15y, find the length of adjacent side.
Solution:
Area of rectangle = 8x2 – 45y2 + 18xy
One side = 4x + 15y
∴ Second (adjacent) side
