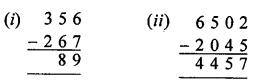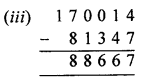ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 2 Whole Numbers Ex 2.2
Question 1.
Fill in the blanks to make each of the following a true statement:
(i) 378 + 1024 = 1024 + …….
(ii) 337 + (528 + 1164) = (337 + ……..) + 1164
(iii) (21 + 18) + ……….. = (21 + 13) + 18
(iv) 3056 + 0 = ……….. = 0 + 3056
Solution:
(i) 378 + 1024= 1024 + 378 (Commutative property of addition)
(ii) 337 + (528 + 1164) = (337 + 528) + 1164 (Associative law of addition)
(iii) (21 + 18) + 13 = (21 + 13) + 18 (Associative law of addition)
(iv) 3056 + 0 = 3056 = 0 + 3056
Question 2.
Add the following numbers and check by reversing the order of addends :
(i) 3189 + 53885
(ii) 33789 + 50311.
Solution:
(i) 3189 + 53885 = 57074
Check 53885 + 3189 = 57074
∴57074
(ii) 33789 + 50311 = 84100
Check 50311 + 33789 = 84100
∴ 84100
Question 3.
By suitable arrangements, find the sum of:
(i) 311,528,289
(ii) 723, 834, 66, 277
(iii) 78, 203, 435, 7197, 422.
Solution:
(i) 311, 528, 289
Sum (311 +289)+ 528
= 600+ 528= 1128
(ii) 723 + 834 + 66 + 277
= (723 + 277) + (834 + 66)
= 1000 + 900 = 1900
(iii) 78, 203, 435, 7197, 422
Sum = (78 + 422) + (203 + 7197) + 435
= 500 + 7400 + 435
= 7900 + 435 = 8335
Question 4.
Fill in the blanks to make each of the following a true statement:
(i) 375 × 57 = 57 × ……….
(ii) (33 × 16) × 25 = 33 × (…….. × 25)
(iii) 37 × 24 = 37 × 18 + 37 × …………
(iv) 7205 × 1 = …………. = 1 × 7205
(v) 366 × 0 =
(vi) …………… × 579 = 0
(vii) 473 × 108 = 473 × 100 + 473 × ………….
(viii) 684 × 97 = 684 × 100 – …………… × 3
(ix) 0 ÷= 5 =
(x) (14 – 14) ÷ 7 = ………….
Solution:
(i) 375 × 57 = 57 × 375 (Commutative property of multiplication)
(ii) 33 × 16) × 25 = 33 × (16 × 25) (Associative law of multiplication)
(iii) 37 × 24 = 37 × 18 + 37 × 6 (Distributive law of multiplication)
(iv) 7205 × 1 = 7205 = 1 × 7205
(v) 366 × 0 = 0
(vi) 0 × 579 = 0
(vii) 473 × 108 = 473 × 100 + 473 × 8
(viii) 684 × 97 = 684 × 100 – 684 × 3
(ix) 0 ÷ 5 = 0
(x) (14 – 14) ÷ 7 = 0
Question 5.
Determine the following products by suitable arrangement:
(i) 4 × 528 × 25
(ii) 625 × 239 × 16
(iii) 125 × 40 × 8 × 25
Solution:
(i) 4 × 528 × 25 = 4 × 25 × 528
= 100 × 528 = 52800
(ii) 625 × 239 × 16 = 625 × 16 × 239
= 10000 × 239 = 2390000
(iii) 125 × 40 × 8 × 25 = 125 × 8 × 40 × 25
= 1000 × 1000 = 1000000
Question 6.
Find the value of the following:
(i) 54279 × 92 + 54279 × 8
(ii) 60678 × 262 – 60678 × 162
Solution:
(i) 54279 × 92 + 54279 × 8
= 54279 (92 + 8)
= 54279 × 100 = 5427900
(ii) 60678 × 262 – 60678 × 162
= 60678 (262 – 162)
= 60678 × 100 = 6067800
Question 7.
Find the following products by using suitable properties:
(i) 739 × 102
(ii) 1938 × 99
(iii) 1005 × 188
Solution:
(i) 739 × 102
= 739 × (100 + 2)
= 739 × 100 + 739 × 2
= 73900 + 1478 = 75378
(ii) 1938 × 99
= 1938 × (100- 1)
= 1938 × 100 – 1938 × 1
= 193800 – 1938 = 191862
(iii) 1005 × 188
= (1000 + 5) × (100 + 88)
= 1000 × 100 + 1000 × 88 + 5 × 100 + 88 × 5
= 100000 + 88000 + 500 + 440 = 188940
Question 8.
Divide 7750 by 17 and check the result by division algorithm.
Solution:
7750 ÷ 17
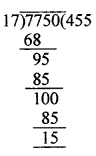
On dividing 7750 by 17, we get
Quotient = 455 and Remainder = 15
Check by division algorithm:
Divident = Divisior × Quotient + Remainder
= 17 × 455 + 15 = 7750
Question 9.
Find the number which when divided by 38 gives the quotient 23 and remainder 17.
Solution:
Divisor = 38,Quotient = 23
Remainder = 17
Dividend = divisor × quotient + remainder
= 38 × 23 + 17 = 874 + 17 = 891
Question 10.
Which least number should be subtracted from 1000 so that the difference is exactly divisible by 35.
Solution:
On dividing 1000 by 35
we get quotient = 28 and remainder 20

So, 20 should be subtracted from 1000.
Question 11.
Which least number should be added to 1000 so that 53 divides the sum exactly.
Solution:

On dividing 1000 by 53, we get quotient = 18 and remainder = 46. To get the remainder 0, we should add 53 – 46 = 7 to 1000.
∴ 7
Question 12.
Find the largest three-digit number which is exactly divisible by 47.
Solution:
Largest three digit no. = 999
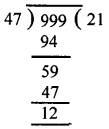
On dividing 999 by 47, we get
Quotient = 21 and Remainder =12
So on subtracting 12 from 999, we get
999 – 12 = 987
Question 13.
Find the smallest five-digit number which is exactly divisible by 254.
Solution:
Smallest 5 digit number = 10000
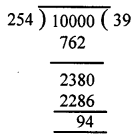
On dividing 10000 by 254, we get
Remainder = 94
So 254 – 94 = 160 should be added to 10000 to get the smallest 5 digit number divisible by 254.
∴ 10000 + 160 = 10160
Question 14.
A vendor supplies 72 litres of milk to a student’s hostel in the morning and 28 litres of milk in the evening every day. If the milk costs?39 per litre, how much money is due to the vendor per day?
Solution:
Supply of milk in morning = 72 litres
Supply of milk in evening = 28 litres
Cost of per litre milk = ₹ 39
Money of per day = ₹ 39 (72 l + 28 l)
= ₹ 39 × 100 = ₹ 3900
Question 15.
State whether the following statements are true (T) or false (F):
(i) If the product of two whole numbers is zero, then atleast one of them will be zero.
(ii) If the product of two whole numbers is 1, then each of them must be equal to 1.
(iii) If a and b are whole numbers such that a ≠ 0 and b ≠ 0, then ab may be zero.
Solution:
(i) True
(ii) True
(iii)False
Question 16.
Replace each * by the correct digit in each of the following:
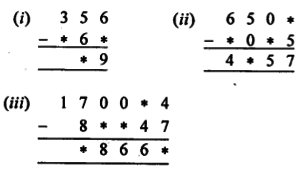
Solution: