ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Ex 13.3
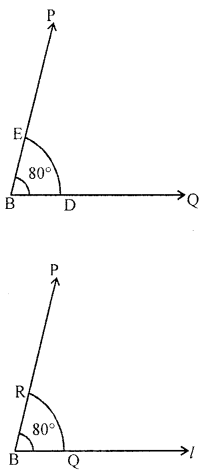
Question 1.
Draw an angle of 80° and make a copy of it using ruler and compass.
Solution:
Steps of construction :
(i) Construct an angle ABC = 80°.
(ii) Take a line l and mark a point D on it.
(iii) Fix the compass pointer on B and
draw an arc which cuts the sides of ∠ABC at D and E.
(iv) Without changing the compass setting,
place the pointer on P and draw an arc which cuts l at Q.
(v) Open the compass equal to length DE.
(vi) Without disturbing the radius on compass,
place its pointer at Q and draw an arc which cuts the previous arc at R.
(vii) Join PR and draw ray PR.
Its gives ∠RPQ which is the required angle
whose measure is equal to the measure of ∠ABC.
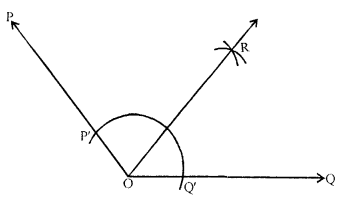
Question 2.
Draw an angle of measure 127° and construct its bisector.
Solution:
Steps of construction :
(i) Draw \(\overline{\mathrm{OQ}}\) of any length.
(ii) Place the centre of the protractor at O and the zero edge along \(\overline{\mathrm{OQ}}\).
(iii) Start with 0 near Q. Mark point P at 127°.
(iv) Join \(\overline{\mathrm{OP}}\). Then, ∠POQ = 127°
(v) With O as centre and using compass,
draw an arc that cuts both rays of ∠POQ.
Label the points of intersection as P’ and Q’.
(vi) With Q’ as centre, draw (in the interior of ∠POQ)
an arc whose radius is more than half the length Q’P’.
(vii) With the same radius and with P’ as centre,
draw another arc in the interior of ∠POQ.
Let the two arcs intersect at R. Then, \(\overline{\mathrm{OR}}\) is the bisector of ∠POQ.
Question 3.
Draw ∠POQ = 64°. Also draw its line of symmetry.
Solution:
Steps of construction :
(i) Draw a ray \(\overline{\mathrm{OQ}}\)
(ii) Place the centre of the protractor at O and the zero edge along \(\overline{\mathrm{OQ}}\).
(iii) Start with 0 near Q. Mark point P at 64°.
(iv) Join \(\overline{\mathrm{OP}}\) . Then, ∠POQ = 64°.
(v) With O as centre and using compass,
draw an arc that cuts both rays of ∠POQ.
Label the points of intersection as P’ and Q’.
(vi) With Q’ as centre, draw (in the interior of ∠POQ)
an arc whose radius is more than half the length Q’P’.
(vii) With the same radius and with P’ as centre,
draw another arc in the interior of ∠POQ.
Let the two arcs intersect at R.
Then, \(\overline{\mathrm{OR}}\) is the bisector of ∠POQ
which is also the line of symmetry of ∠POQ as ∠POR = ∠ROQ.
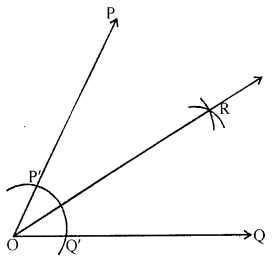
Question 4.
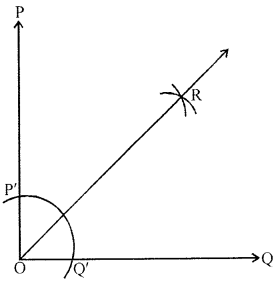
Draw a right angle and construct its bisector.
Solution:
Steps of construction :
(i) Draw a ray OQ.
(ii) Place the centre of the protractor at O and the zero edge along \(\overline{\mathrm{OQ}}\).
(iii) Start with 0 near Q. Mark point P at 90°.
(iv) Join \(\overline{\mathrm{OP}}\). Then, ∠POQ = 90°
(v) With 0 as centre and using compass,
draw an arc that cuts both rays of ∠POQ.
Label the points of intersection as P’ and Q’.
(vi) With Q’ as centre, draw (in the interior of ∠POQ)
an arc whose radius is more than half the length Q’P’.
(vii) With the same radius and with P’ as centre,
draw another arc in the interior of ∠POQ.
Let the two arcs intersect at R.
Then, \(\overline{\mathrm{OR}}\) is the bisector of ∠POQ.
Question 5.
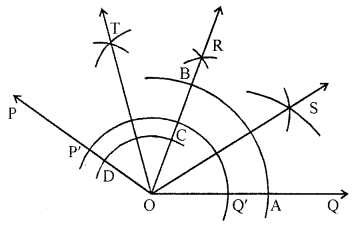
Draw an angle of 152° and divide it into four equal parts.
Solution:
Steps of construction :
(i) Draw a ray \(\overline{\mathrm{OQ}}\).
(ii) Place the centre of the protractor at O and the zero edge along \(\overline{\mathrm{OQ}}\).
(iii) Start with 0 near Q. Mark a point P at 152°.
(iv) Join OP. Then, ∠POQ =152°
(v) With O as centre and using compass,
draw an arc that cuts both rays of ∠POQ.
Label the points of intersection as P’ and Q’.
(vi) With Q’ as centre, draw (in the interior of ∠POQ)
an arc whose radius is more than half the length Q’P’.
(vii) With the same radius and with P’ as centre,
draw another arc in the interior of ∠POQ.
Let the two arcs intersect at R. Then, \(\overline{\mathrm{OR}}\) is the bisector of ∠POQ.
(viii)With O as centre and using compasses,
draw an arc that cuts both rays of ∠ROQ.
Label the points of intersection as B and A.
(ix) With A as centre, draw (in the interior of ∠ROQ)
an arc whose radius is more than half the length AB.
(x) With the same radius and with B as centre,
draw another arc in the interior of ∠ROQ.
Let the two arcs intersect at S. Then, \(\overline{\mathrm{OS}}\) is the bisector of ∠ROQ.
(xi) With O as centre and using compass,
draw an arc that cuts both rays of ∠POR.
Label the points of intersection as D and C.
(xii) With C as centre, draw (in the interior of ∠POR)
an arc whose radius is more than half the length CD.
(xiii) With the same radius and with D as centre,
draw another arc in the interior of ∠POR.
Let the two arcs intersect at T.
Then, \(\overline{\mathrm{OT}}\) is the bisector of ∠POR.
Thus, \(\overline{\mathrm{OS}}\), \(\overline{\mathrm{OR}}\) and \(\overline{\mathrm{OT}}\) divide ∠POQ = 152° into four equal parts.
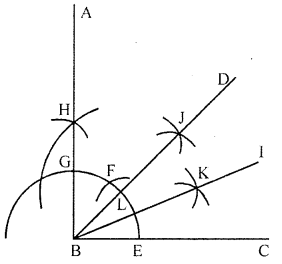
Question 6.
Draw an angle of measure 45° and bisect it.
Solution:
Steps of construction :
(i) Draw a straight line BC.
(ii) With B as a centre and any suitable radius,
draw an arc to meet BC at E.
(iii) With E as centre and same radius
draw an arc to meet the previous arc at G.
(iv) With G and F as centre and same radius
draw another arc to meet the first arc at H.
(v) With H and E as centre draw two arcs of equal radius less than \(\frac{1}{2}\) GE.
(vi) Cutting each other at J joined BJ and produce it to D.
(vii) With L and E as centre draw two arcs of equal radius less than \(\frac{1}{2}\) LE.
(viii) Cutting each other at K joined BK and produce it to I.
(ix) Measuring angle ∠IBC = 22.5°