Selina Concise Mathematics Class 9 ICSE Solutions Co-ordinate Geometry
ICSE SolutionsSelina ICSE Solutions
APlusTopper.com provides step by step solutions for Selina Concise Mathematics Class 9 ICSE Solutions Chapter 26 Co-ordinate Geometry. You can download the Selina Concise Mathematics ICSE Solutions for Class 9 with Free PDF download option. Selina Publishers Concise Mathematics for Class 9 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Download Formulae Handbook For ICSE Class 9 and 10
Selina ICSE Solutions for Class 9 Maths Chapter 26 Co-ordinate Geometry
Exercise 26(A)
Solution 1:

Solution 2:
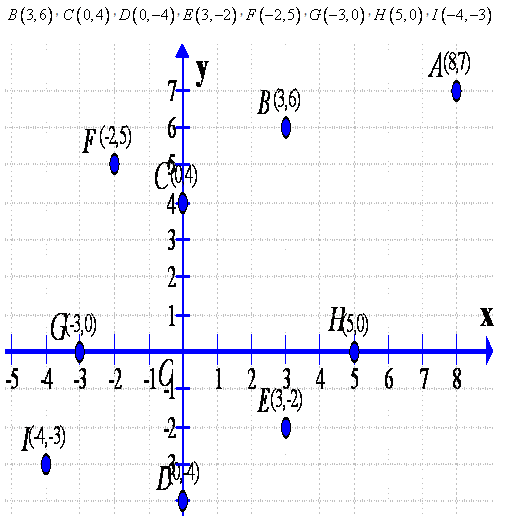
On the graph paper, let us draw the co-ordinate axes XOX’ and YOY’ intersecting at the origin O. With proper scale, mark the numbers on the two co-ordinate axes.
Now for the point A(8,7)
Step I
Starting from origin O, move 8 units along the positive direction of X axis, to the right of the origin O
Step II
Now from there, move 7 units up and place a dot at the point reached. Label this point as A(8,7)
Similarly plotting the other points
Solution 3:

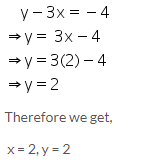
Solution 4:
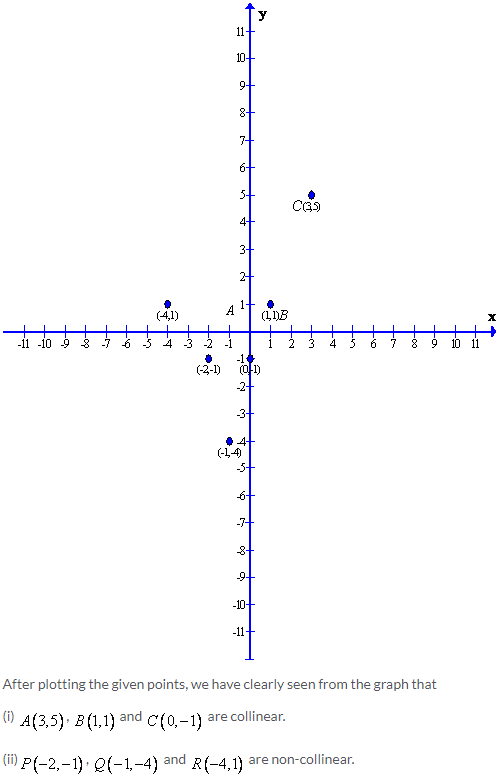
(i) The abscissa is 2
Now using the given graph the co-ordinate of the given point A is given by (2,2)
(ii) The ordinate is 0
Now using the given graph the co-ordinate of the given point B is given by (5,0)
(iii) The ordinate is 3
Now using the given graph the co-ordinate of the given point C and E is given by (-4,3)& (6,3)
(iv) The ordinate is -4
Now using the given graph the co-ordinate of the given point D is given by (2,-4)
(v) The abscissa is 5
Now using the given graph the co-ordinate of the given point H, B and G is given by (5,5) ,(5,0) & (5,-3)
(vi)The abscissa is equal to the ordinate.
Now using the given graph the co-ordinate of the given point I,A & H is given by (4,4),(2,2) & (5,5)
(vii)The ordinate is half of the abscissa
Now using the given graph the co-ordinate of the given point E is given by (6,3)
Solution 5:
(i)The ordinate of a point is its x-co-ordinate.
False.
(ii)The origin is in the first quadrant.
False.
(iii)The y-axis is the vertical number line.
True.
(iv)Every point is located in one of the four quadrants.
True.
(v)If the ordinate of a point is equal to its abscissa; the point lies either in the first quadrant or in the second quadrant.
False.
(vi)The origin (0,0) lies on the x-axis.
True.
(vii)The point (a,b) lies on the y-axis if b=0.
False
Solution 6:
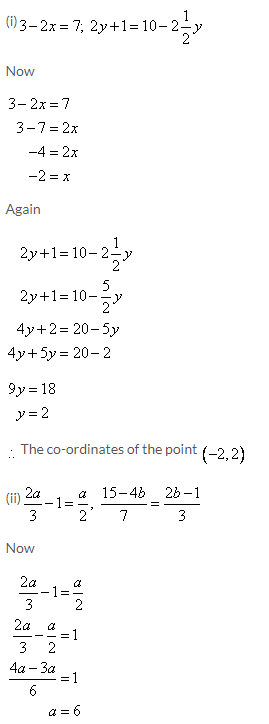
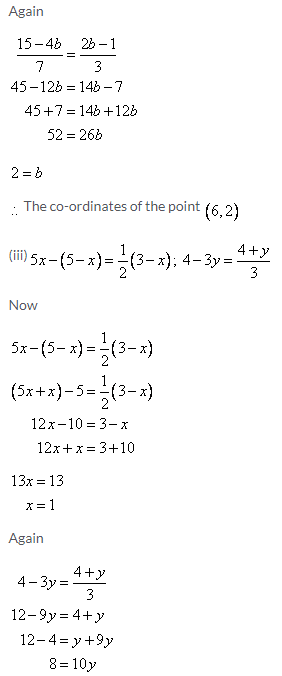

Solution 7:
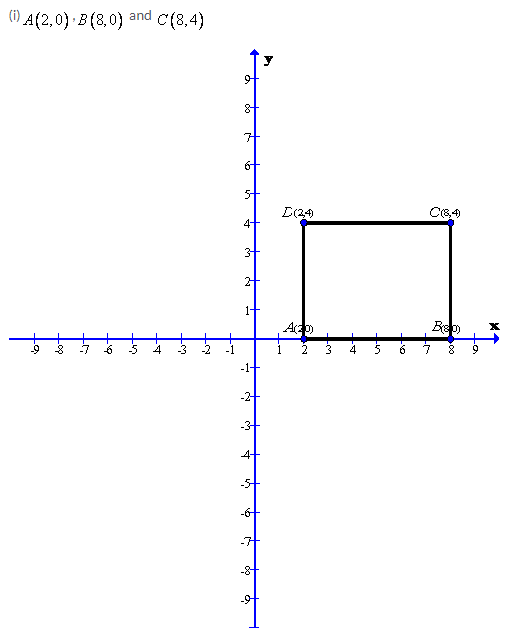
After plotting the given points A(2,0), B(8,0) and C(8,4) on a graph paper; joining A with B and B with C. From the graph it is clear that the vertical distance between the points B(8,0) and C(8,4) is 4 units, therefore the vertical distance between the points A(2,0) and D must be 4 units. Now complete the rectangle ABCD
As is clear from the graph D(2,4)
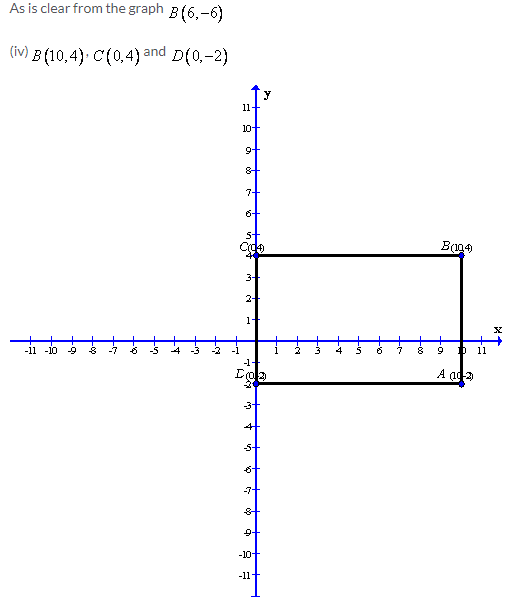
(ii)A(4,2), B(-2,-2) and D(4,-2)
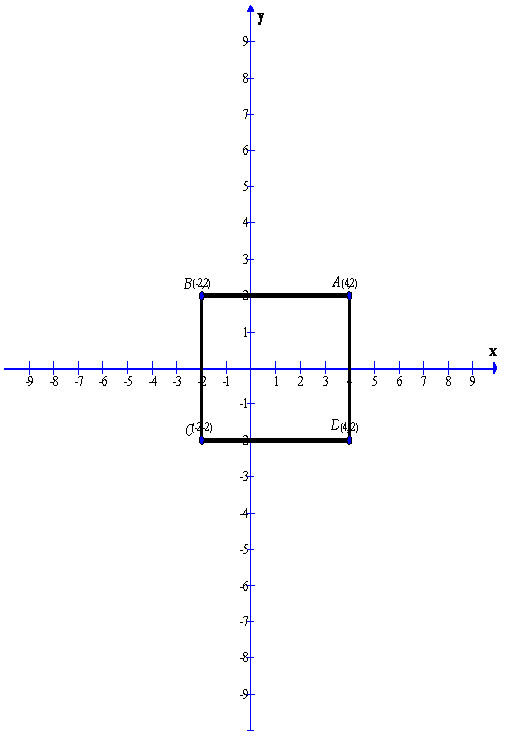
After plotting the given points A(4,2), B(-2,2) and D(4,-2) on a graph paper; joining A with B and A with D. From the graph it is clear that the vertical distance between the points A(4,2) and D(4,-2) is 4 units and the horizontal distance between the points A(4,2) and B(-2,2) is 6 units , therefore the vertical distance between the points B(-2,2)and C must be 4 units and the horizontal distance between the points B(-2,2) and C must be 6 units. Now complete the rectangle ABCD
As is clear from the graph C(-2,2)
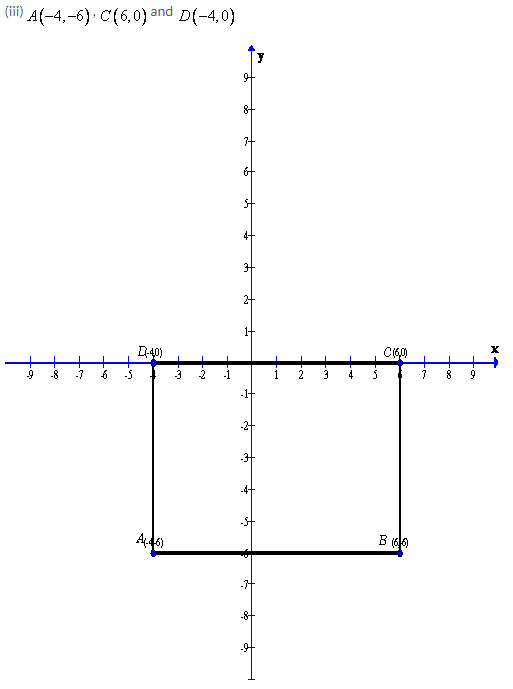


Solution 8:
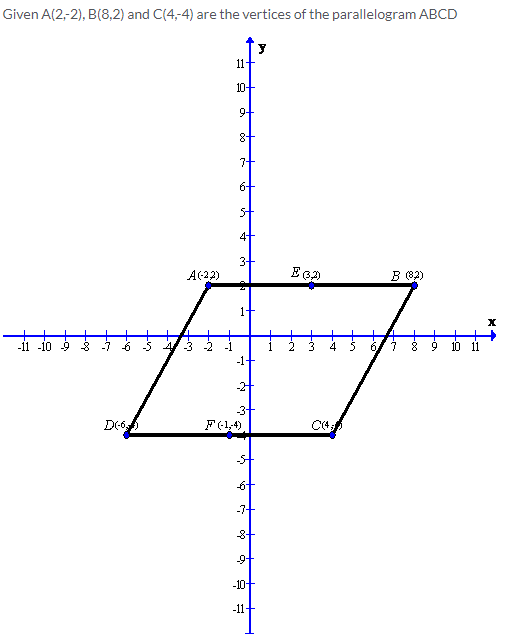
After plotting the given points A(2,-2), B(8,2) and C(4,-4) on a graph paper; joining B with C and B with A . Now complete the parallelogram ABCD.
As is clear from the graph D(-6,4)
Now from the graph we can find the mid points of the sides AB and CD.
Therefore the co-ordinates of the mid-point of AB is E(3,2) and the co-ordinates of the mid-point of CD is F(-1,-4)
Solution 9:
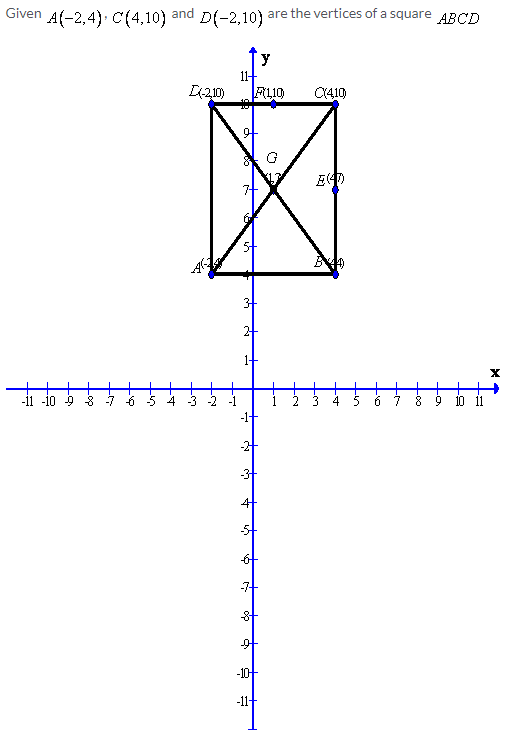

Solution 10:
Solution 11:
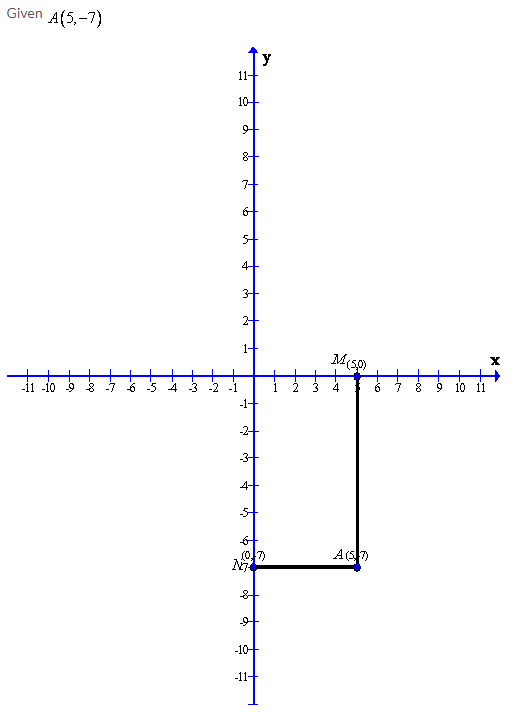

Solution 12:
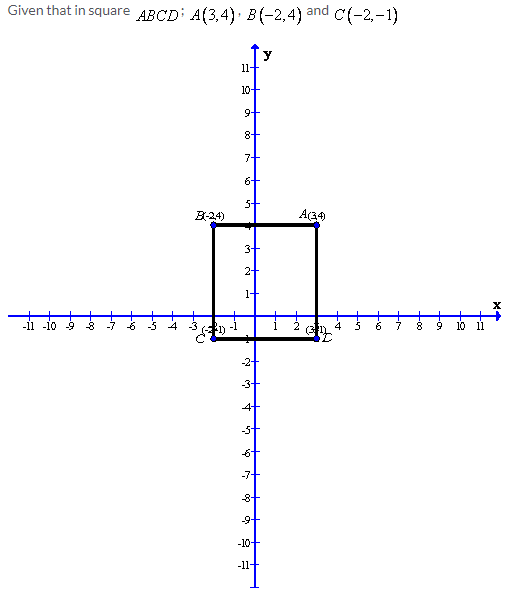
Solution 13:

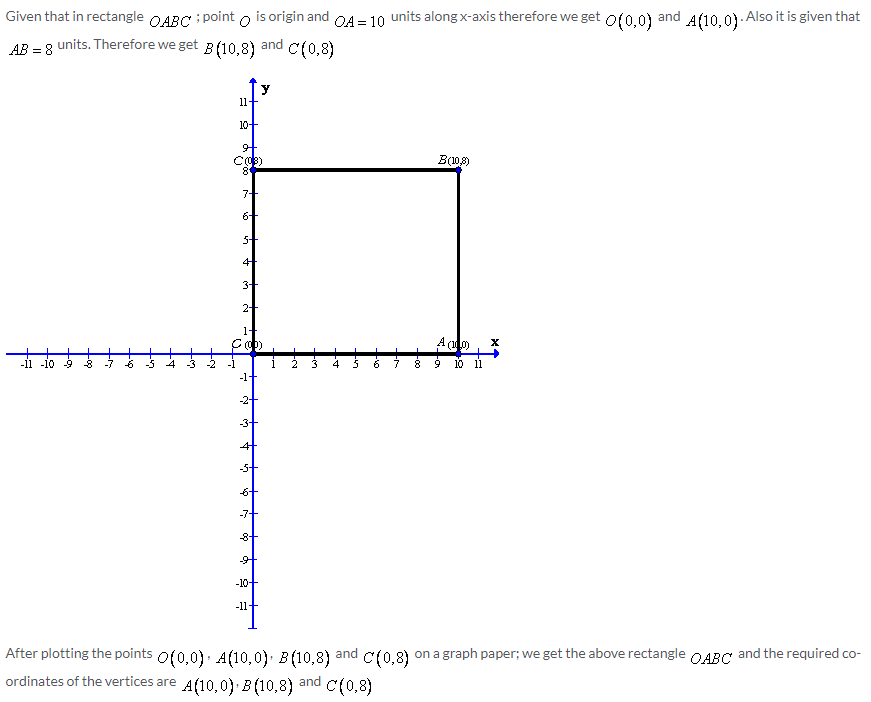
Exercise 26(B)
Solution 1:
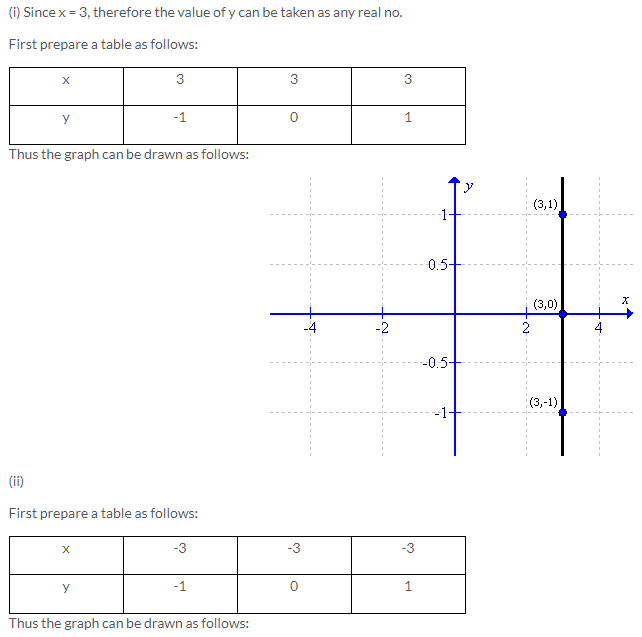
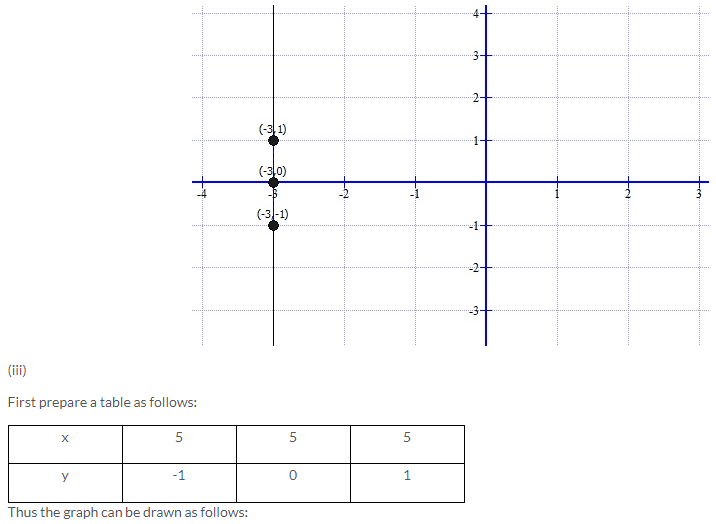
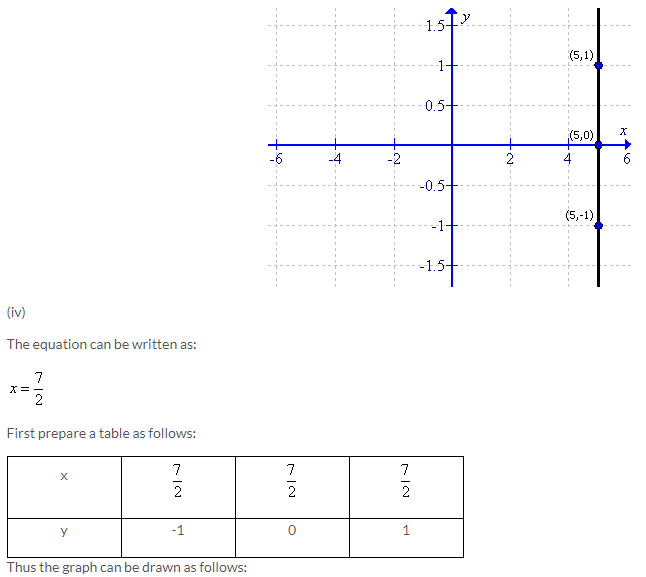
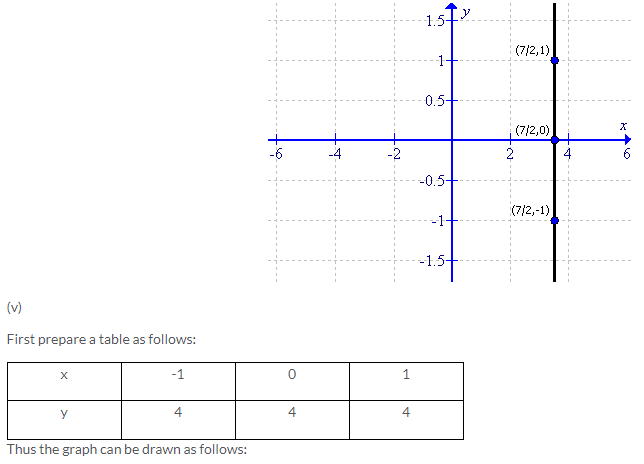
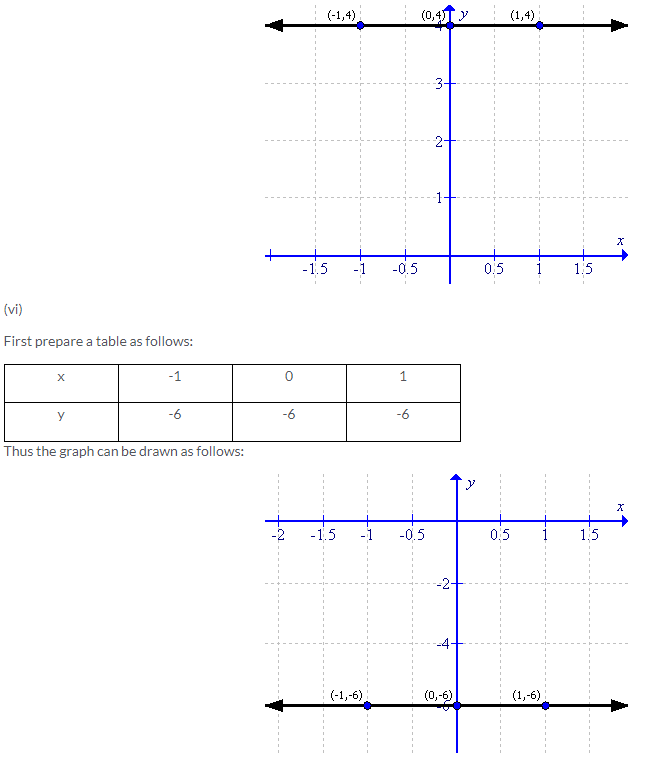
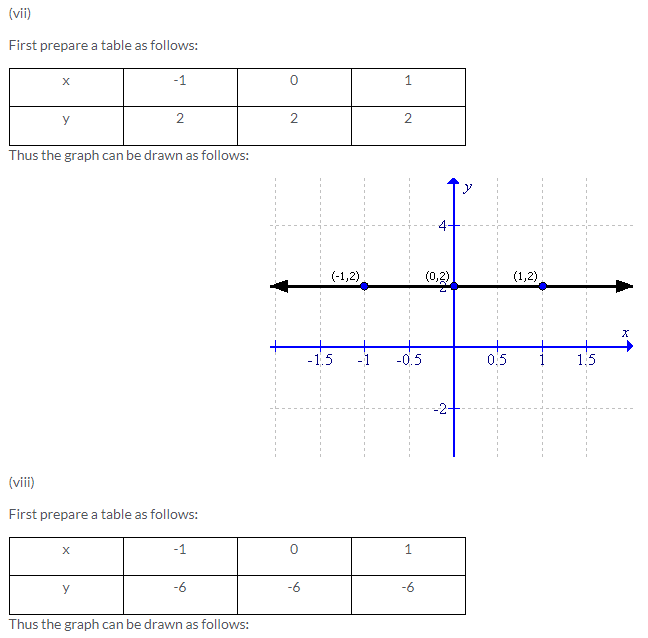
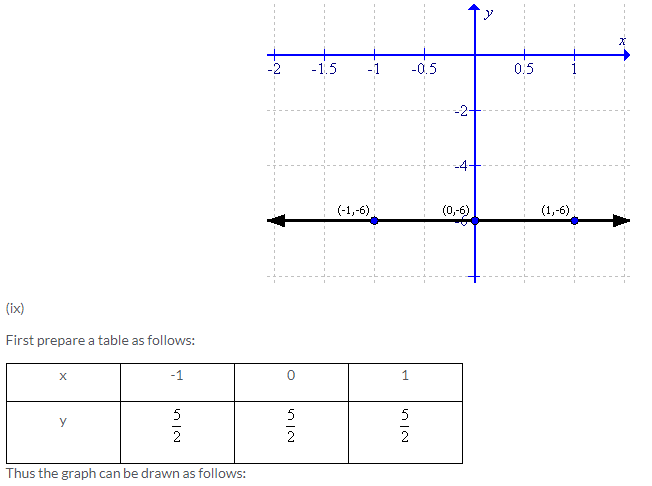
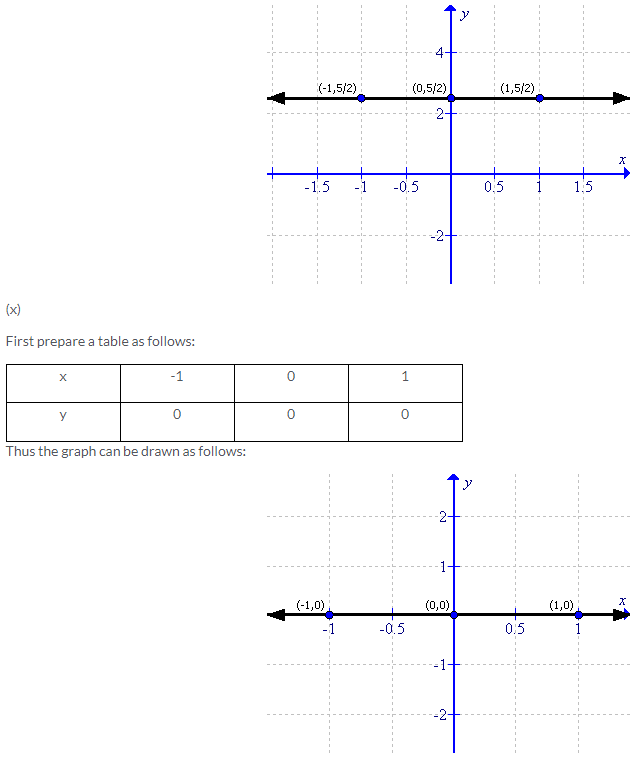
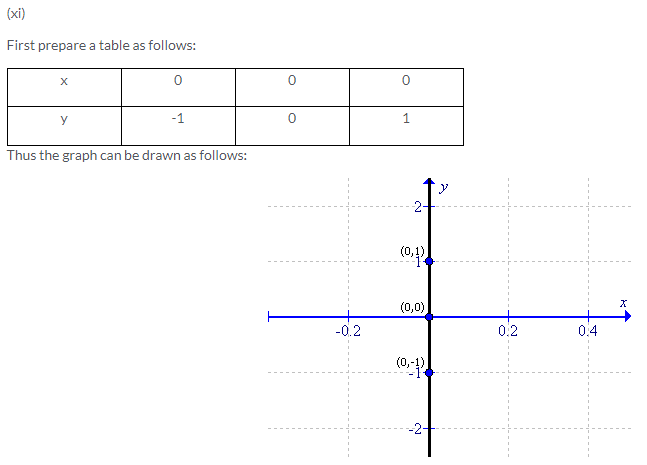
Solution 2:
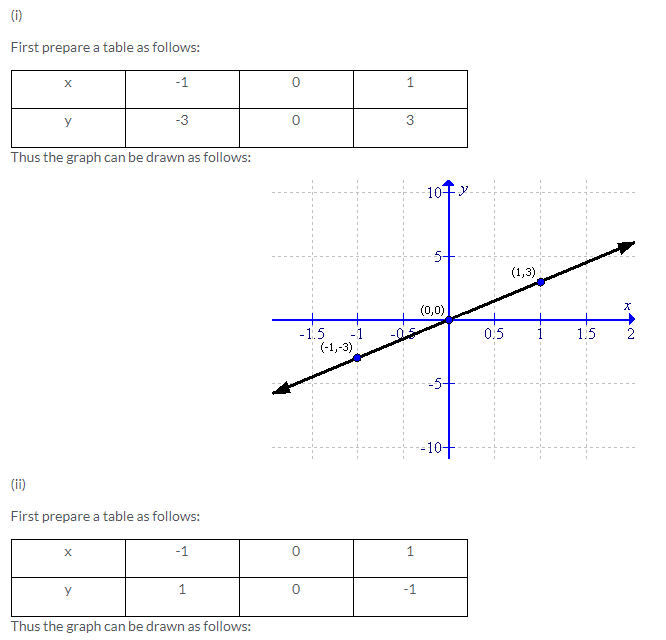
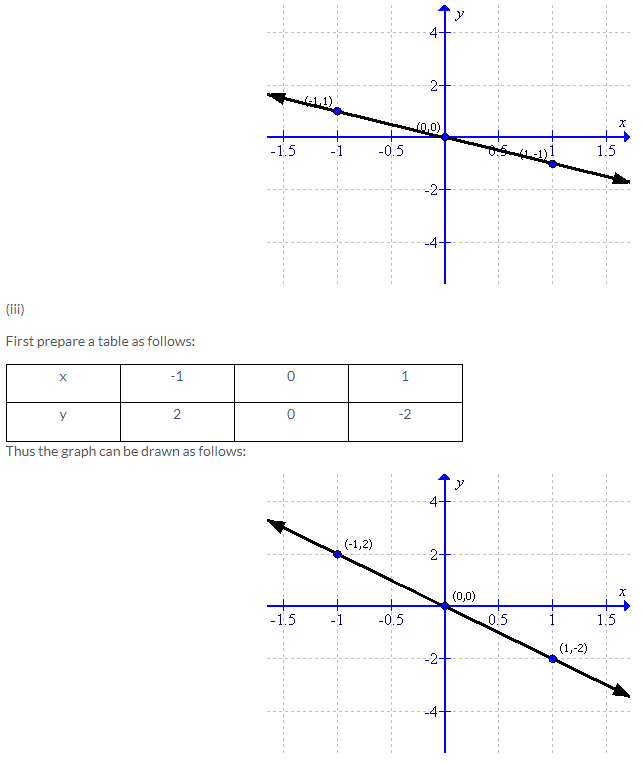
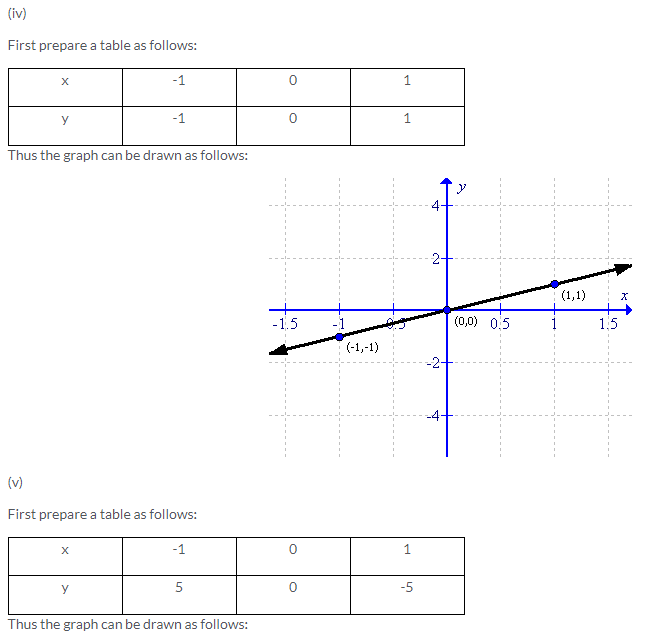
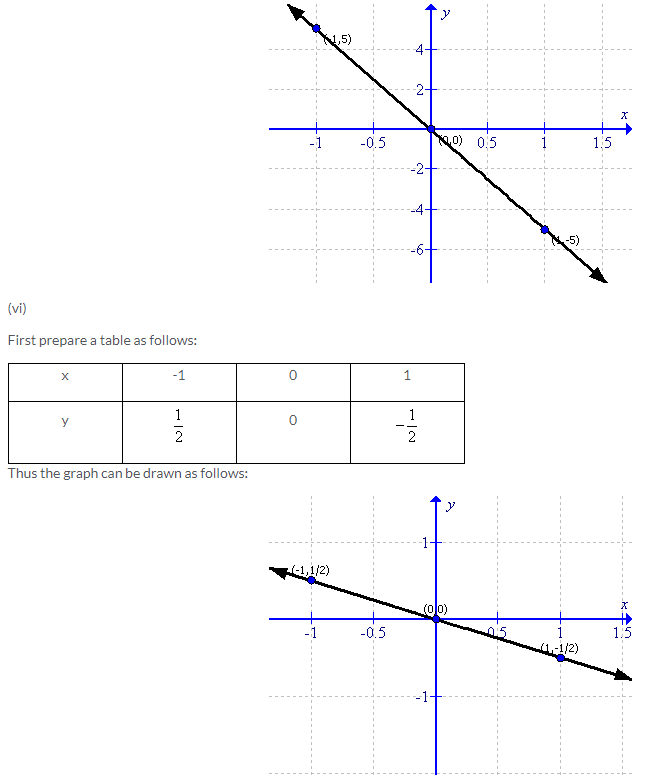
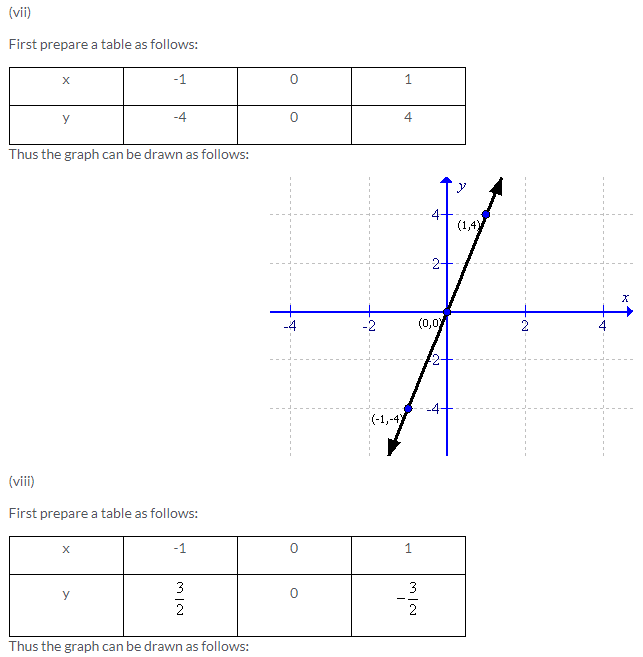
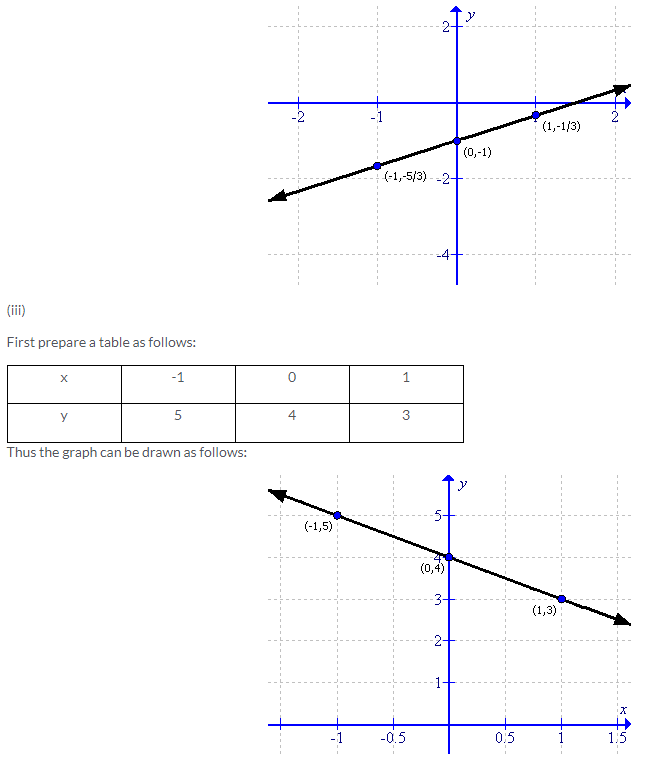
Solution 3:
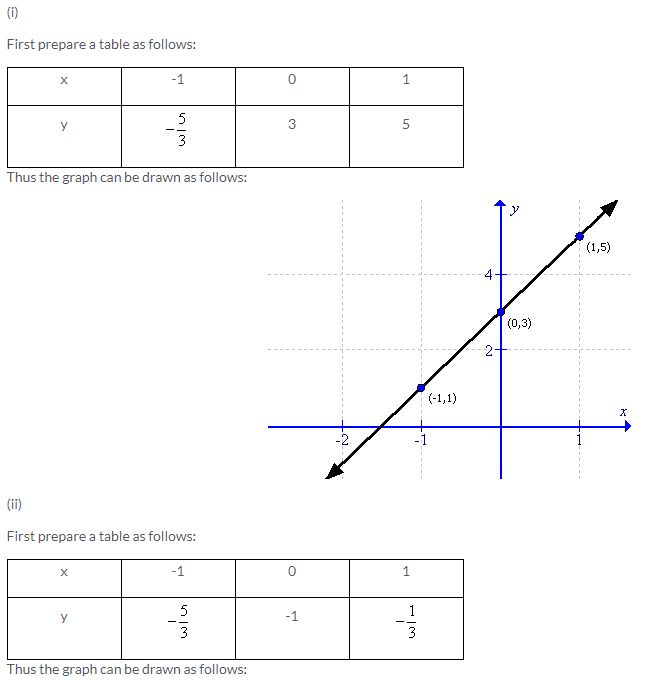
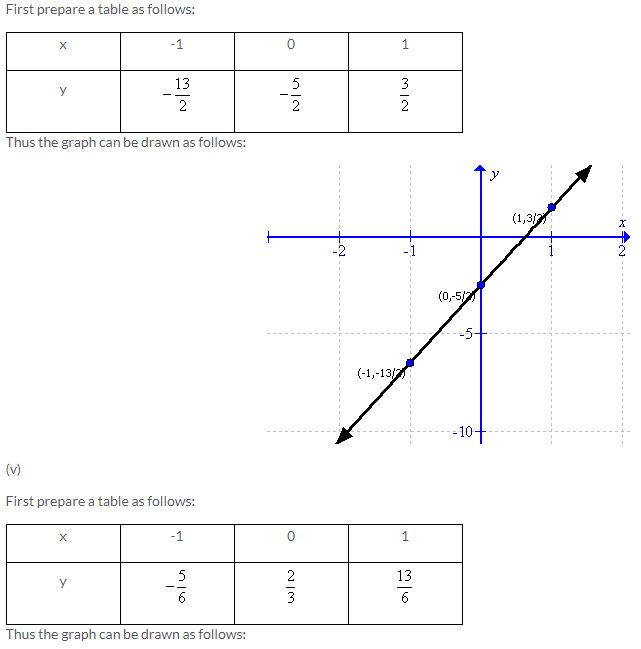
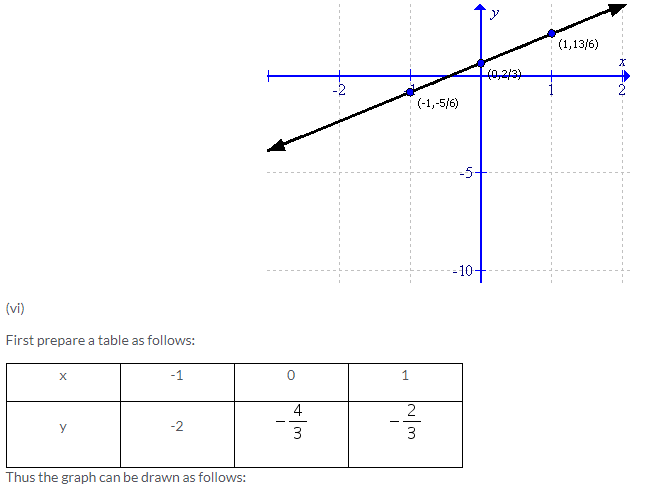
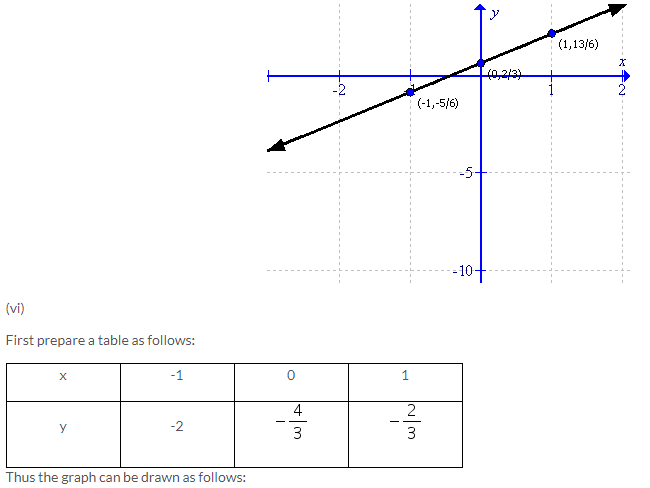
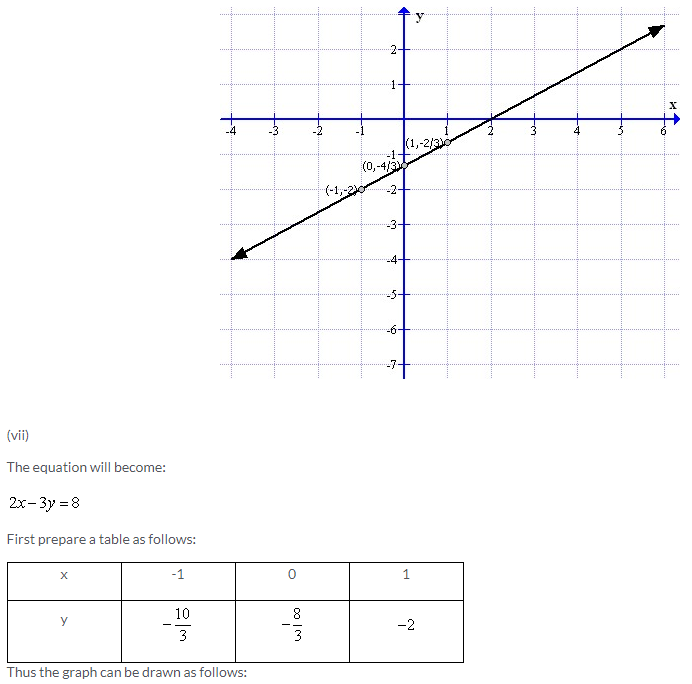
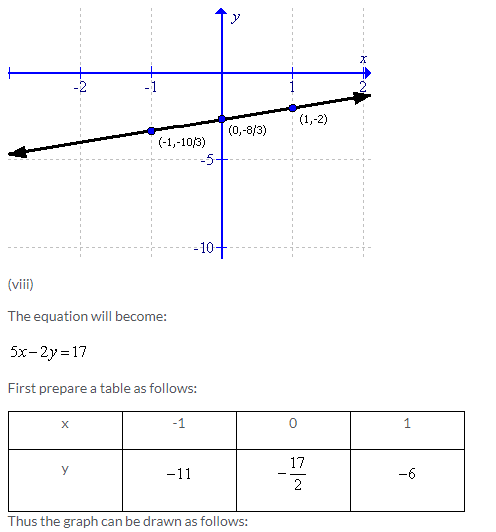
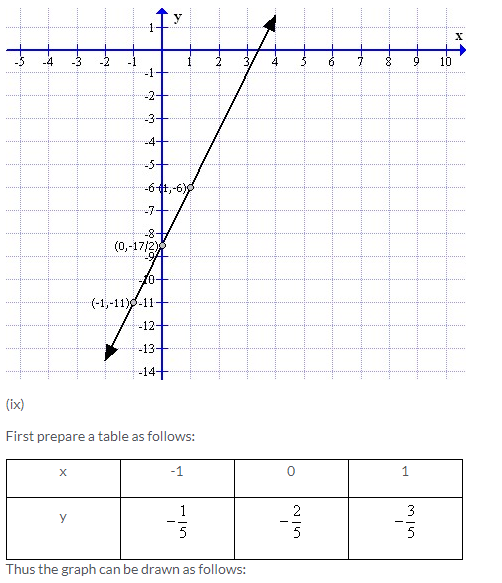
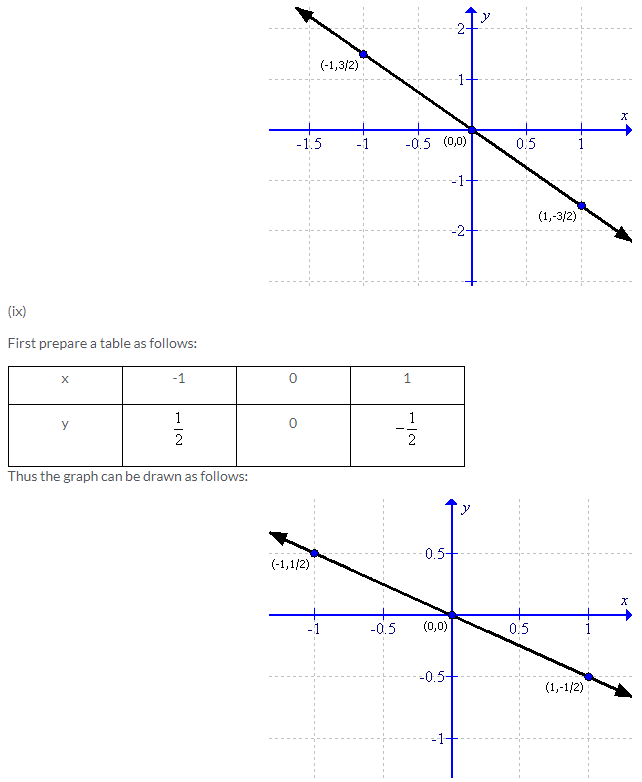
Solution 4:
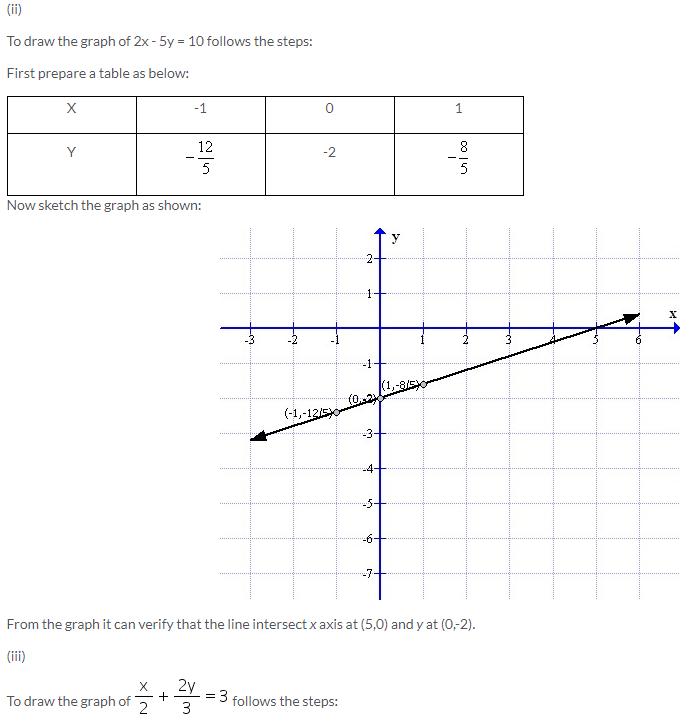
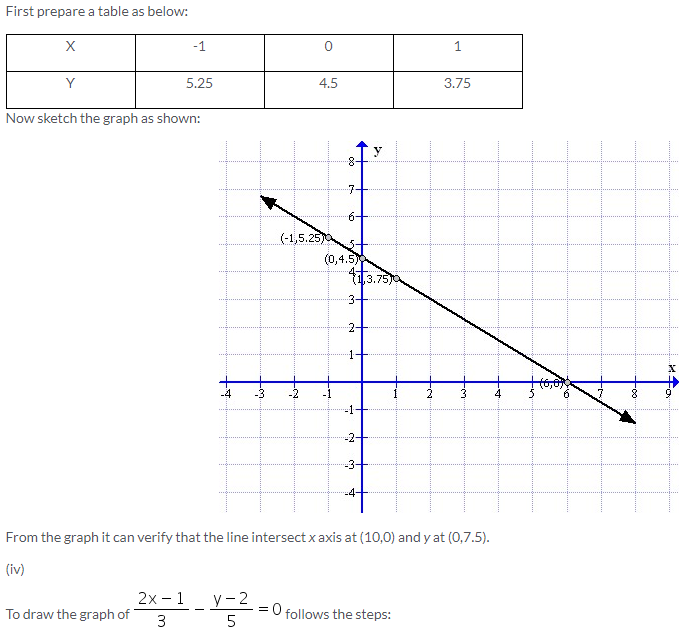
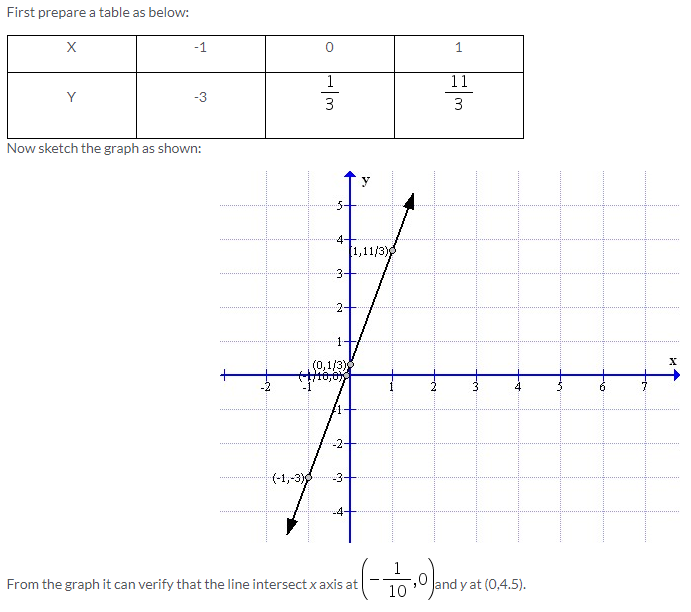
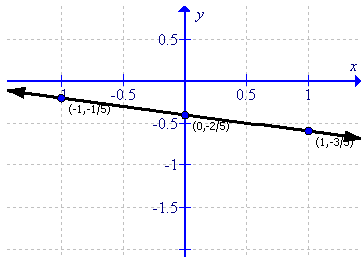
Solution 5:
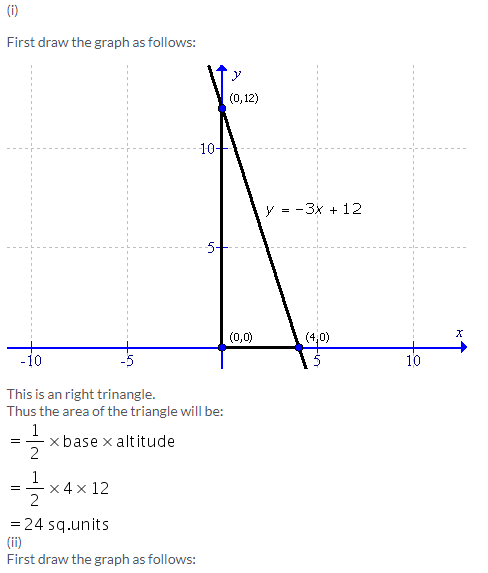
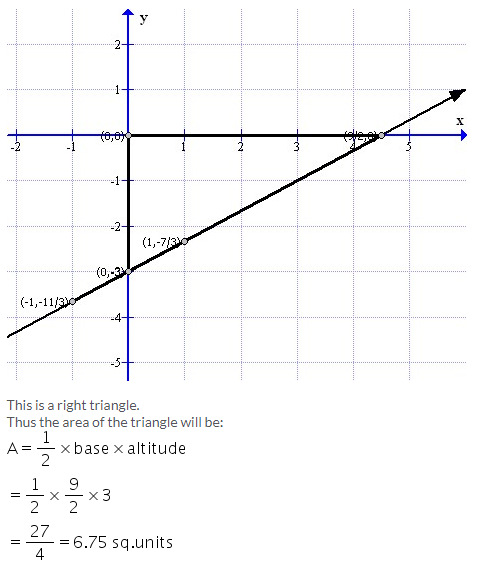
Solution 6:
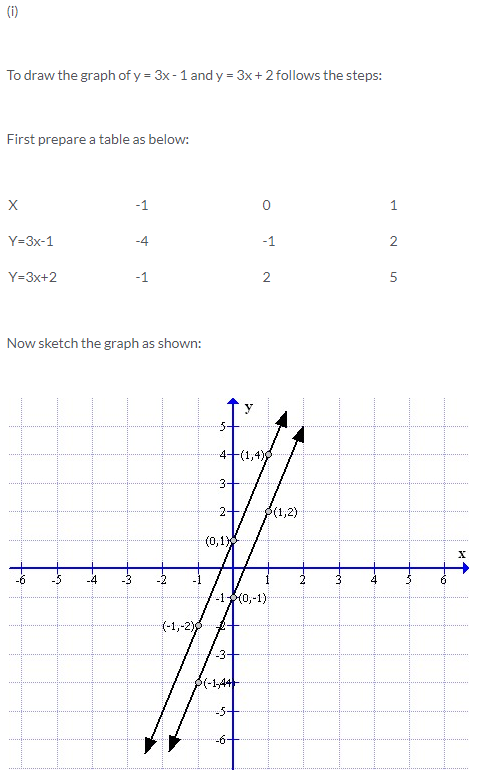
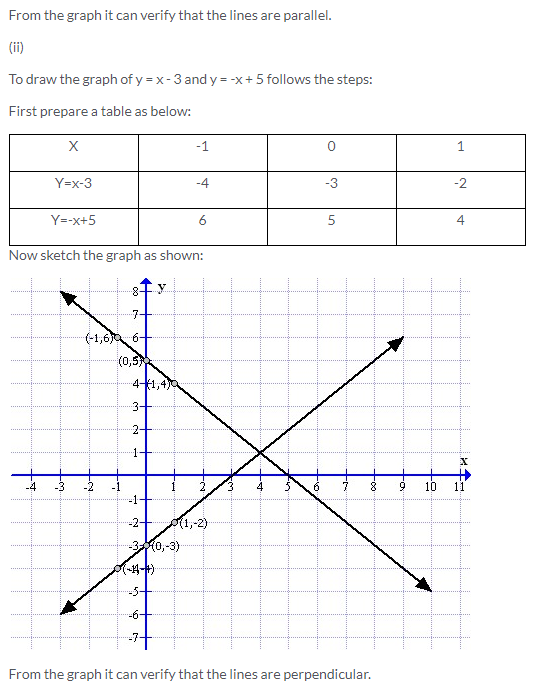
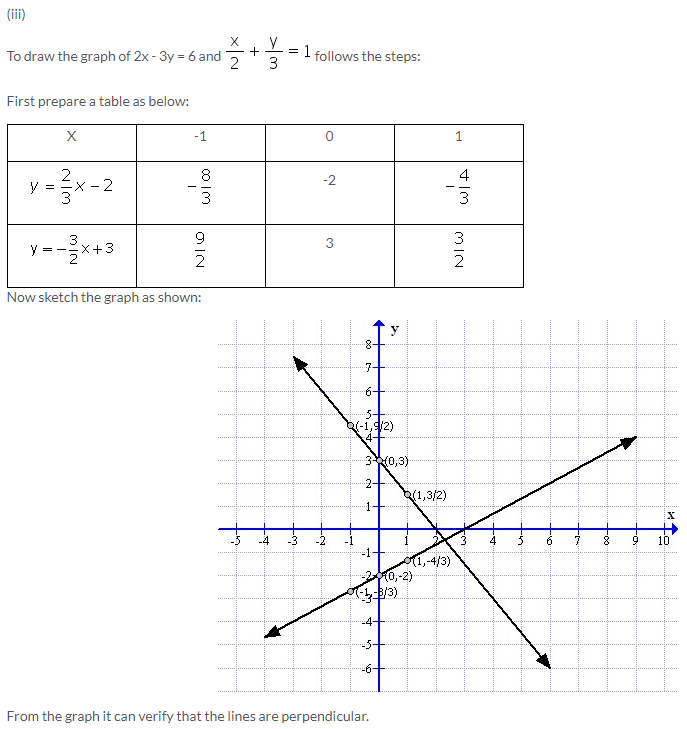
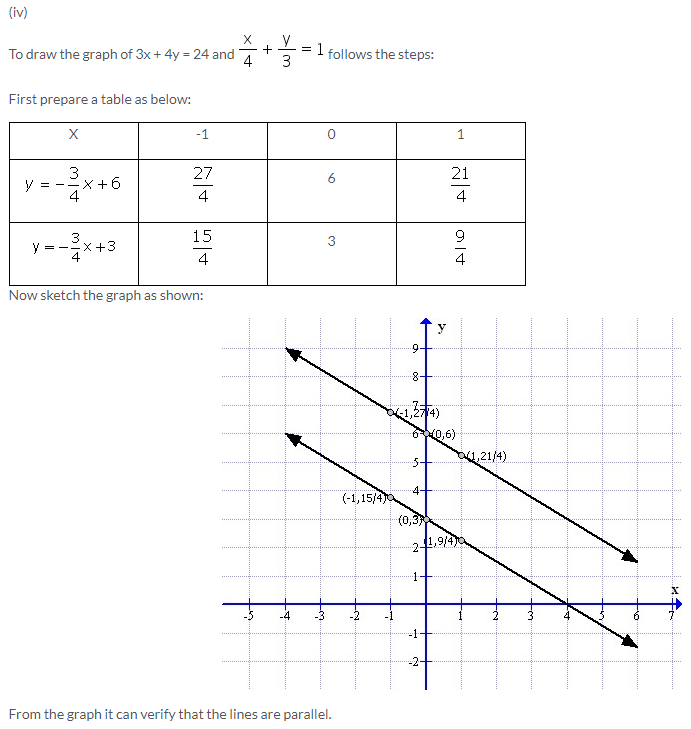
Solution 7:
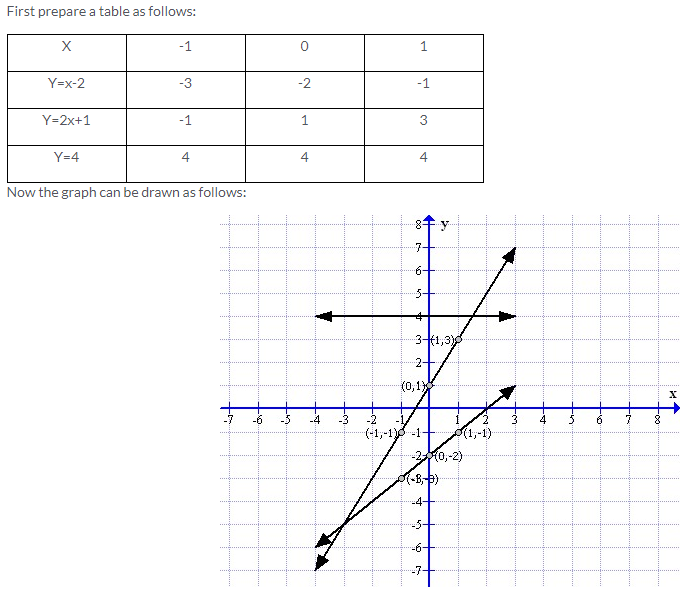
Solution 8:
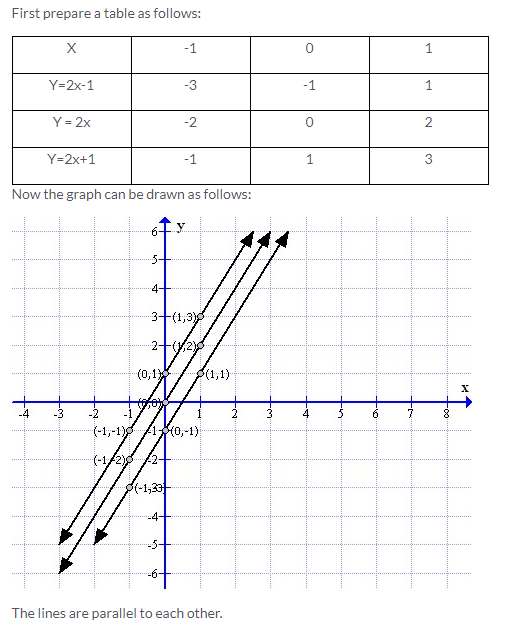
Solution 9:
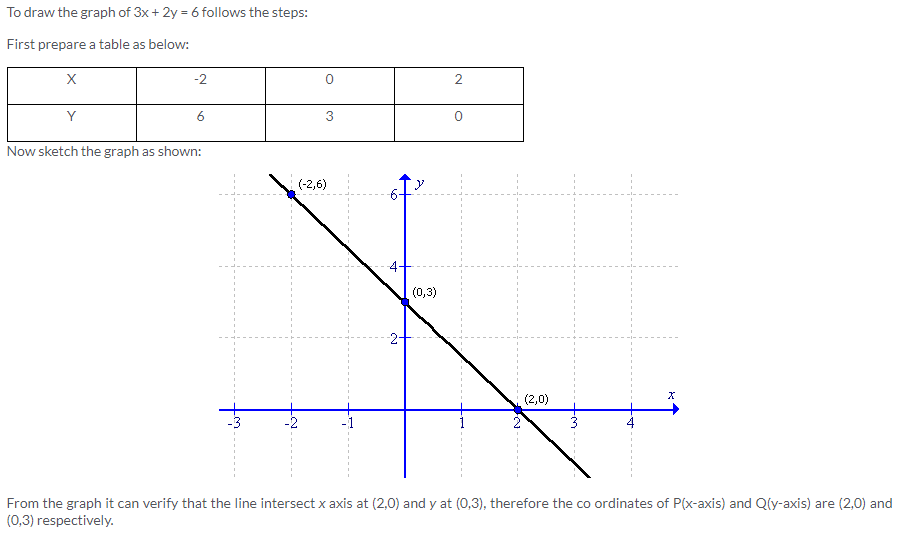
Solution 10:
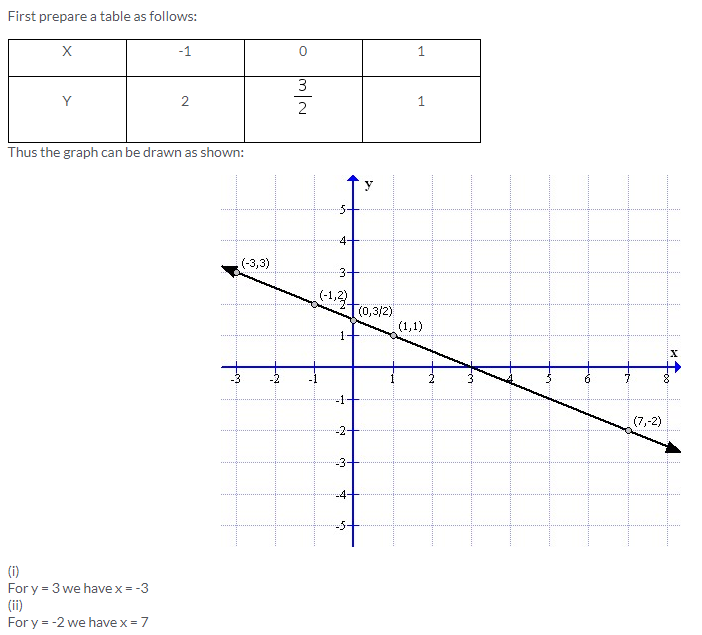
Solution 11:
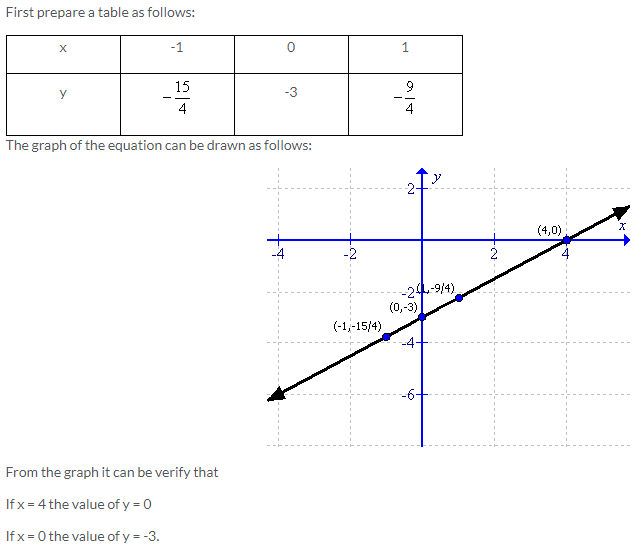
Solution 12:
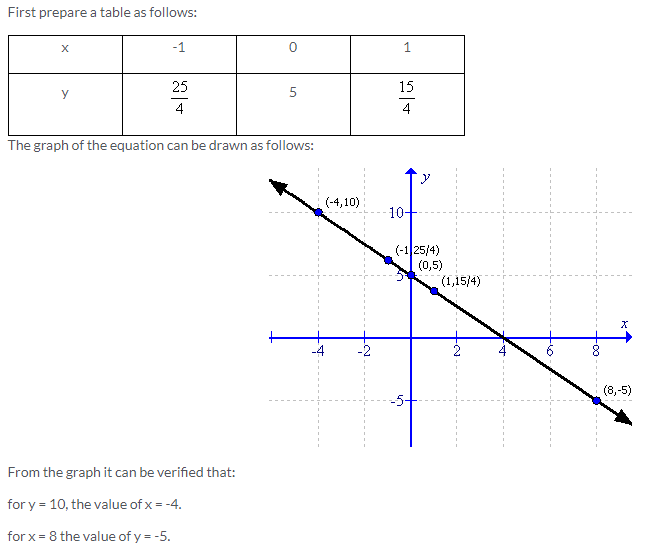
Solution 13:

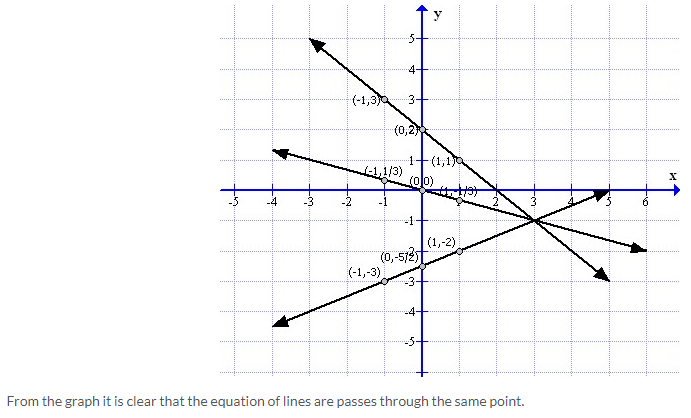
Exercise 26(C)
Solution 1:
The angle which a straight line makes with the positive direction of x-axis (measured in anticlockwise direction) is called inclination o the line.
The inclination of a line is usually denoted by θ
(i)The inclination is θ = 45°
(ii) The inclination is θ = 135°
(iii) The inclination is θ = 30°
Solution 2:
(i)The inclination of a line parallel to x-axis is θ = 0°
(ii)The inclination of a line perpendicular to x-axis is θ = 90°
(iii) The inclination of a line parallel to y-axis is θ = 90°
(iv) The inclination of a line perpendicular to y-axis is θ = 0°
Solution 3:

Solution 4:

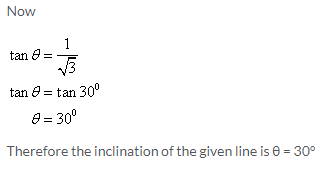
Solution 5:

Solution 6:

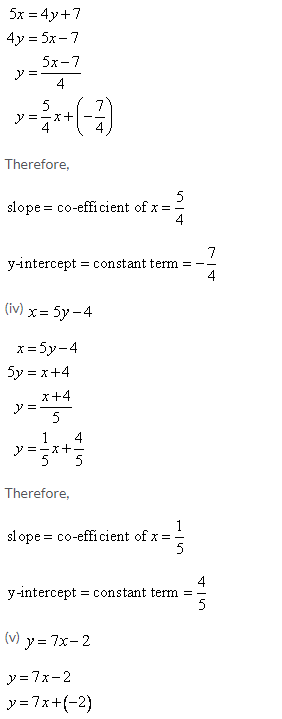

Solution 7:


Solution 8:
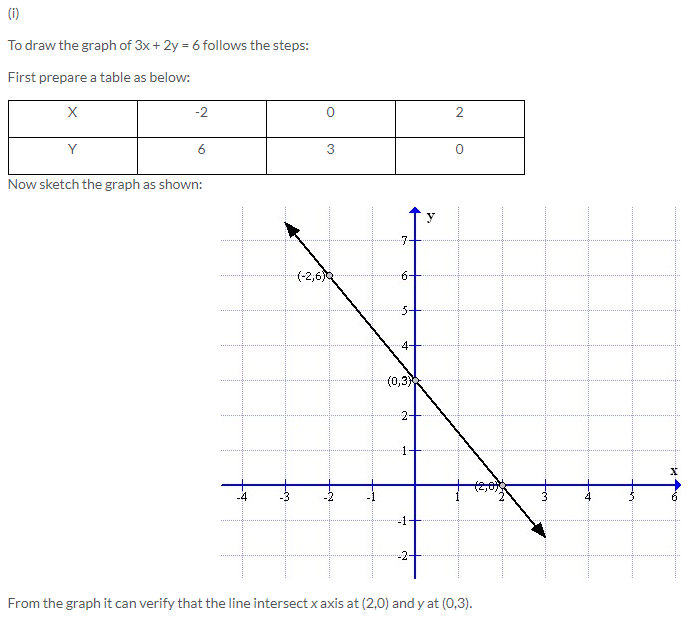
Given line is 3x + 4y = 12
The graph of the given line is shown below.
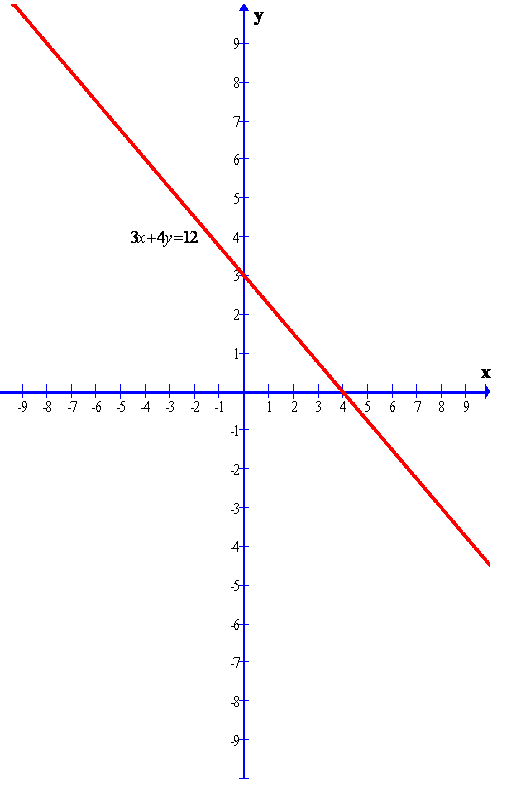
Clearly from the graph we can find the y-intercept.
The required y-intercept is 3.
Solution 9:
Given line is
2x – 3y – 18 = 0
The graph of the given line is shown below.
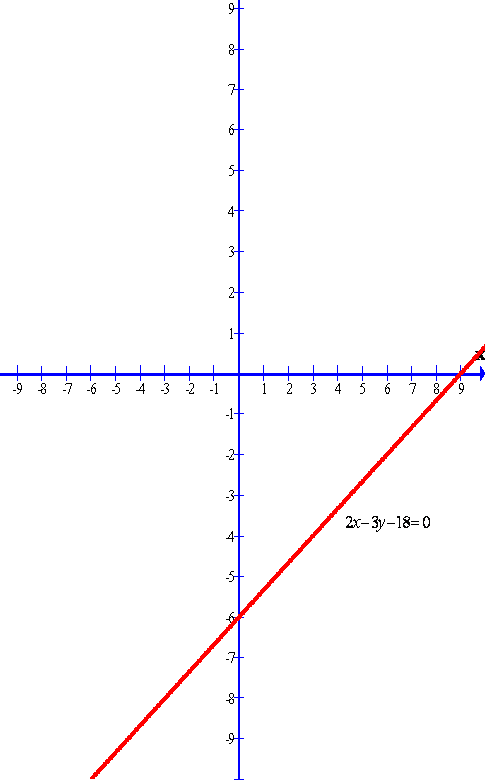
Clearly from the graph we can find the y-intercept.
The required y-intercept is -6
Solution 10:
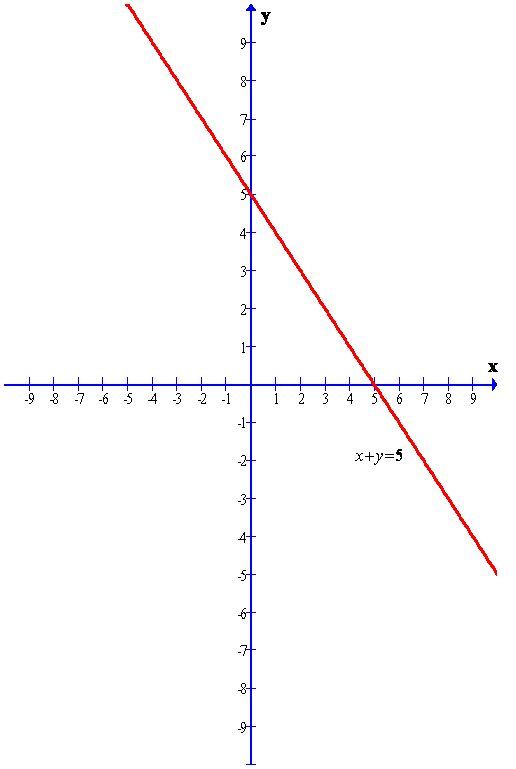
Given line is
x + y = 5
The graph of the given line is shown below.

More Resources for Selina Concise Class 9 ICSE Solutions