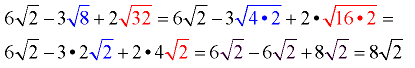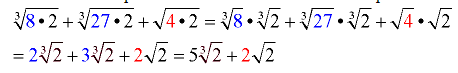Radicals Archives

Radicals | Simplification, Properties, Addition and Multiplication of Radicals

A radical or the principal nth root of k:
k, the radicand, is a real number.
n, the index, is a positive integer greater than one.

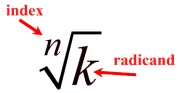
radpic1

Properties of Radicals:

Properties-of-radicals

Simplifying Radicals:
Radicals that are simplified have:
– no fractions left under the radical.
– no perfect power factors in the radicand , k.
– no exponents in the radicand , k, greater than the index, n.
– no radicals appearing in the denominator
of a fractional answer.

Examples: (The following examples demonstrate various solution methods.)

Simplify: Factor the radicand to isolate the perfect power factor(s), which will allow them to be removed from under the radical. You will need to remember your rules for working with exponents in order to isolate the perfect powers.

perfect squares
4, 9, 16, 25, 36, …
x², x⁴, x⁶, x⁸, …
x²y², x²y⁴, 16x⁶y⁸, …
powers are “even”

perfect cubes
8, 27, 64, 125, …
x³, x⁶, x⁹, x¹², …
x³y³, x³y⁶, 27x⁶y⁹, …
powers are “multiples of 3”

To add radicals

simplify first if possible, and add “like” radicals.

adding-radicals

To multiply radicals

multiplying -radicals -2

Addition and Subtraction of Radicals

(For this lesson, the term “radical” will refer only to “square root”.)
When adding or subtracting radicals, you must use the same concept as that of adding or subtracting “like” variables.
In other words, the radicals must be the same before you add (or subtract) them.

Since the radicals are the same, simply add the numbers in front of the radicals (do NOT add the numbers under the radicals).

Since the radicals are not the same, and both are in their simplest form, there is no way to combine these values. The answer is the same as the problem.

Warning: If the radicals in your problem are different, be sure to check to see if the radicals can be simplified. Often times, when the radicals are simplified, they become the same radical and can then be added or subtracted. Always simplify, if possible, before deciding upon your answer.

Example 1: Add: 2√3 + 4√75
At first glance, it appears that combining these terms under addition is not possible since the radicals are not the same. But if we look further, we can simplify the second term so it will be a “like” radical: