Selina Concise Physics Class 9 ICSE Solutions Upthrust in Fluids, Archimedes’ Principle and Floatation
ICSE SolutionsSelina ICSE Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 9 Physics Chapter 5 Upthrust in Fluids, Archimedes’ Principle and Floatation. You can download the Selina Concise Physics ICSE Solutions for Class 9 with Free PDF download option. Selina Publishers Concise Physics for Class 9 ICSE Solutions all questions are solved and explained by expert teachers as per ICSE board guidelines.
Download Formulae Handbook For ICSE Class 9 and 10
Selina ICSE Solutions for Class 9 Physics Chapter 5 Upthrust in Fluids, Archimedes’ Principle and Floatation
Exercise 5(A)
Solution 1S.
When a body is partially or wholly immersed in a liquid, an upward force acts on it. This upward force is known as an upthrust.
Upthrust can be demonstrated by the following experiment:
Take an empty can and close its mouth with an airtight stopper. Put it in a tub filled with water. It floats with a large part of it above the surface of water and only a small part of it below the surface of water. Push the can into the water. You can feel an upward force and you find it difficult to push the can further into water. It is noticed that as the can is pushed more and more into the water, more and more force is needed to push the can further into water, until it is completely immersed. When the can is fully inside the water, a definite force is still needed to keep it at rest in that position. Again, if the can is released in this position, it is noticed that the can bounces back to the surface and starts floating again.
Solution 2S.
Buoyant force on a body due to a liquid acts upwards at the centre of buoyancy.
Solution 3S.
The property of a liquid to exert an upward force on a body immersed in it is called buoyancy.
Solution 4S.
The upward force exerted on a body by the fluid in which it is submerged is called the upthrust. Its S.I. unit is ‘newton’.
Solution 5S.
A liquid contained in a vessel exerts pressure at all points and in all directions. The pressure at a point in a liquid is the same in all directions – upwards, downwards and sideways. It increases with the depth inside the liquid.
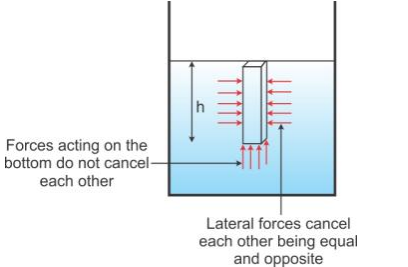
When a body is immersed in a liquid, the thrusts acting on the side walls of the body are neutralized as they are equal in magnitude and opposite in direction. However, the magnitudes of pressure on the upper and lower faces are not equal. The difference in pressure on the upper and lower faces cause a net upward force (= pressure x area) or upthrust on the body.
It acts at the centre of buoyancy.
Solution 6S.
Upthrust due to water on block when fully submerged is more than its weight. Density of water is more than the density of cork; hence, upthrust due to water on the block of cork when fully submerged in water is more than its weight.
Solution 7S.
A piece of wood if left under water comes to the surface of water because the upthrust on body due to its submerged part is equal to its own weight.
Solution 8S.
Experiment to show that a body immersed in a liquid appears lighter:
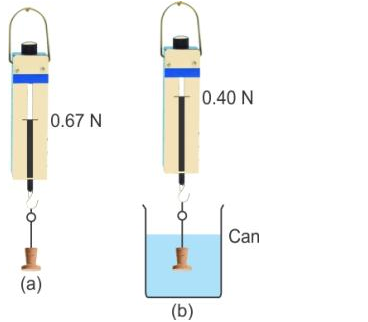
Take a solid body and suspend it by a thin thread from the hook of a spring balance as shown in the above figure (a). Note its weight. Above figure (a) shows the weight as 0.67 N.
Then, take a can filled with water. Immerse the solid gently into the water while hanging from the hook of the spring balance as shown in figure (b). Note its weight. Above figure (b) shows the weight as 0.40 N.
The reading in this case (b) shall be less than the reading in the case (a), which proves that a body immersed in a liquid appears to be lighter.
Solution 9S.
The readings in the spring balance decreases.
As the cylinder is immersed in the jar of water, an upward force acts on it, which is in opposition to the weight component of the cylinder. Hence the cylinder appears to be lighter.
Solution 10S.
A body shall weigh more in vacuum because in vacuum, i.e. in absence of air, no upthrust will act on the body.
Solution 11S.
Upthrust on a body depends on the following factors:
- Volume of the body submerged in the liquid or fluid.
- Density of liquid or fluid in which the body is submerged.
Solution 12S.
Larger the volume of body submerged in liquid, greater is the upthrust acting on it.
Solution 13S.
A stone falls faster.
Because the volume of stone is less than the volume of bunch of feathers of the same mass, the upthrust due to air on stone is less than that on the bunch of feathers, and hence, the stone falls faster.
However, in vacuum, both shall fall together because there will be no upthrust.
Solution 14S.
F2 > F1; Sea water is denser than river water; therefore, the upthrust due to sea water will be greater than that due to river water at the same level. This shall make the body to appear lighter in the sea water.
Solution 15S.
Observation: Volume of a block of wood immersed in glycerine is smaller as compared to the volume of block immersed in water.
Explanation: Density of glycerine is more than that of water. Hence, glycerine exerts more upthrust on the block of wood than water, causing it to float in glycerine with a smaller volume.
Solution 16S.
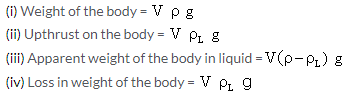
Solution 17S.
Solution 18S.
(a) Both have equal volumes.
(b) Bounce back to the surface.
(c) More than
Solution 19S.
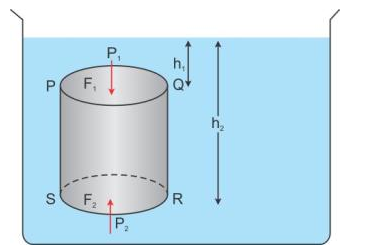
Consider a cylindrical body PQRS of cross-sectional area A immersed in a liquid of density ρ as shown in the figure above. Let the upper surface PQ of the body is at a depth h1 while its lower surface RS is at depth h2 below the free surface of liquid.
At depth h1, the pressure on the upper surface PQ,
P1 = h1 ρg.
Therefore, the downward thrust on the upper surface PQ,
F1 = Pressure x Area = h1 ρgA ……………….(i)
At depth h2, pressure on the lower surface RS,
P2 = h2 ρg
Therefore, the upward thrust on the lower surface RS,
F2 = Pressure x Area = h2 ρgA …………………(ii)
The horizontal thrust at various points on the vertical sides of body get balanced because the liquid pressure is the same at all points at the same depth.
From the above equations (i) and (ii), it is clear that F2 > F1 because h2 > h1 and therefore, body will experience a net upward force.
Resultant upward thrust or buoyant force on the body,
FB = F2 – F1
= h2 ρgA – h1 ρgA
= A (h2 – h1) ρg
However, A (h2 – h1) = V, the volume of the body is submerged in a liquid.
Therefore, upthrust FB = V ρg.
Now, V g = Volume of solid immersed x Density of liquid x Acceleration due to gravity
= Volume of liquid displaced x Density of liquid x Acceleration due to gravity
= Mass of liquid displaced x Acceleration due to gravity
= Weight of the liquid displaced by the submerged part of the body
Thus, Upthrust FB = weight of the liquid displaced by the submerged part of the body…..(iii)
Now, let us take a solid and suspend it by a thin thread from the hook of a spring balance and note its weight.
Then take a eureka can and fill it with water up to its spout. Arrange a measuring cylinder below the spout of the eureka can as shown. Immerse the solid gently in water. The water displaced by the solid is collected in the measuring cylinder.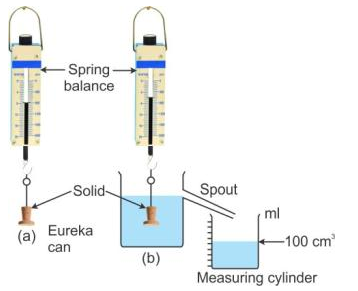
When the water stops dripping through the spout, note the weight of the solid and volume of water collected in the measuring cylinder.
From the diagram, it is clear that
Loss in weight (Weight in air – Weight in water) = Volume of water displaced.
Or, Loss in weight = Volume of water displaced x 1 gcm-3 [Because the density of water = 1 gcm-3]
Or, Loss in weight = Weight of water displaced ……………(iv)
From equations (iii) and (iv),
Loss in weight = Upthrust or buoyant force
Solution 20S.
Since the spheres have the same radius, both will have an equal volume inside water, and hence, the upthrust acted by water on both the spheres will be the same.
Hence, the required ratio of upthrust acting on two spheres is 1:1.
Solution 21S.
Sphere of iron will sink.
Density of iron is more than the density of water, so the weight of iron sphere will be more than the upthrust due to water in it; thus, it causes the iron sphere to sink.
Density of wood is less than the density of water, so the weight of sphere of wood shall be less than the upthrust due to water in it. So, the sphere of wood will float with a volume submerged inside water which is balanced by the upthrust due to water.
Solution 22S.
The bodies of average density greater than that of the liquid sink in it. While the bodies of average density equal to or smaller than that of liquid float on it.
Solution 23S.
(i) The body will float if ρ ≤ ρL
(ii) The body will sink if ρ > ρL
Solution 24S.
It is easier to lift a heavy stone under water than in air because in water, it experiences an upward buoyant force which balances the actual weight of the stone acting downwards. Thus, due to upthrust there is an apparent loss in the weight of the heavy stone, which makes it lighter in water, and hence easy to lift.
Solution 25S.
Archimedes’ principle states that when a body is immersed partially or completely in a liquid, it experiences an upthrust, which is equal to the weight of liquid displaced by it.
Solution 26S.
Let us take a solid and suspend it by a thin thread from the hook of a spring balance and note its weight (Fig a).
Then take a eureka can and fill it with water up to its spout. Arrange a measuring cylinder below the spout of the eureka can as shown. Immerse the solid gently in water. The water displaced by the solid gets collected in the measuring cylinder.
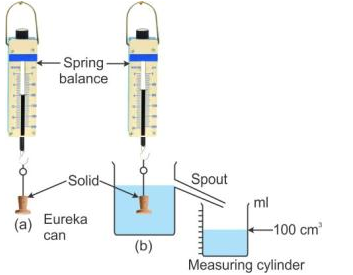
When water stops dripping through the spout, note the weight of the solid and volume of water collected in the measuring cylinder.
From diagram, it is clear that
Loss in weight (Weight in air – weight in water) = 300 gf – 200 gf = 100 gf
Volume of water displaced = Volume of solid = 100 cm3
Because density of water = 1 gcm-3
Weight of water displaced = 100 gf = Upthrust or loss in weight
This verifies Archimedes’ principle.
Solution 1M.
Turpentine
Solution 2M.
N
Solution 3M.
ρ > ρL
Solution 1N.
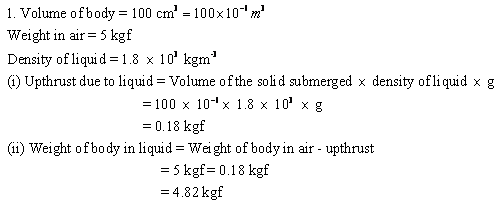
Solution 2N.
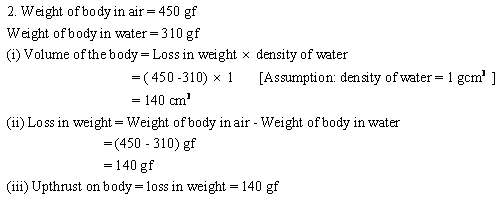
Solution 3N.
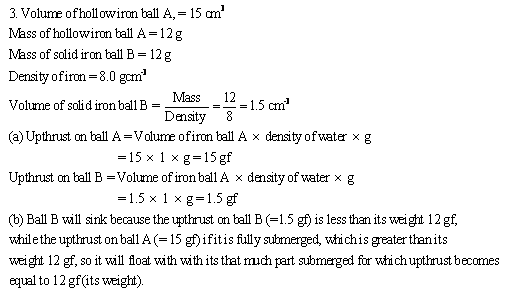
Solution 4N.
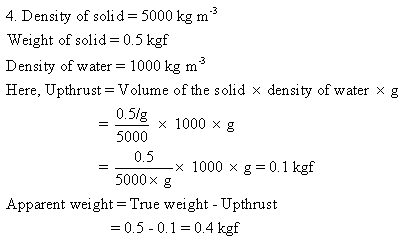
Solution 5N.
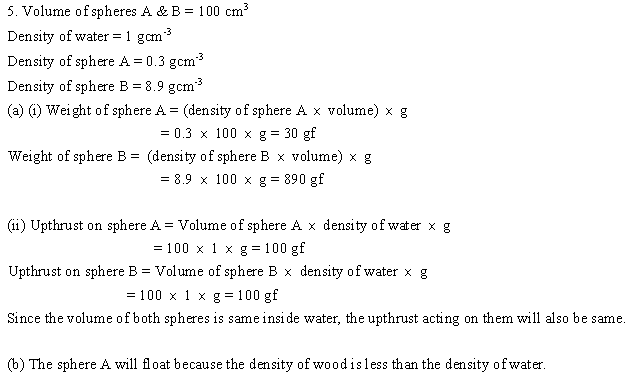
Solution 6N.

Solution 7N.
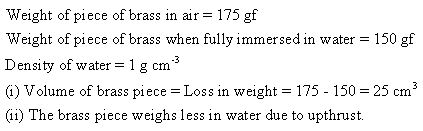
Solution 8N.

Solution 9N.
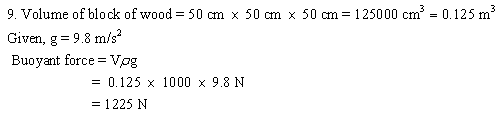
Solution 10N.

Exercise 5(B)
Solution 1S.
The density of a substance is its mass per unit volume.
Solution 2S.
(i) The C.G.S. unit of density is gcm-3.
(ii) The S.I. unit of density is kgm-3.
Solution 3S.
1 gcm-3 = 1000 kgm-3
Solution 4S.
It means the mass of 1 m-3 of iron is 7800 kg.
Solution 5S.
Density of water at 4°C in S.I. units is 1000 kgm-3.
Solution 6S.
(i) Mass of a metallic body remains unchanged with increase in temperature.
(ii) Volume of metallic body increases with an increase in temperature.
(iii) Density (= Mass/volume) of a metallic body decreases with an increase in temperature.
Solution 7S.
On heating from 0°C, the density of water increases up to 4°C and then decreases beyond 4°C.
Solution 8S.
(i) Volume, (ii) kg m-3, (iii) 1000 and (iv) 1000
Solution 9S.
The relative density of a substance is the ratio of density of that substance to the density of water at 4°C.
Solution 10S.
Relative density is the ratio of two similar quantities; thus, it has no unit.
Solution 11S.
Density of a substance is the ratio of its mass to its volume but R.D. of a substance is the ratio of density of that substance to the density of water at 4°C.
Solution 12S.
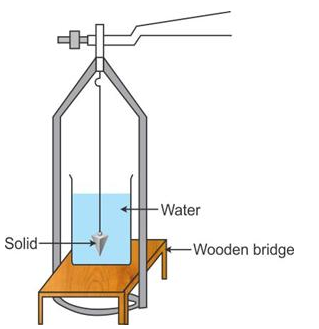
Steps:
- With the help of a physical balance, find the weight, W1 of the given solid.
- Immerse the solid completely in a beaker filled with water such that it does not touch the walls and bottom of beaker, and find the weight W2 of solid in water.
Observations:
Loss in weight of solid when immersed in water = (W1 – W2) gf
R.D. = Weight of solid in air/Loss of weight of solid in water
R.D. = W1/(W1 – W2).
If the solid is soluble in water, then instead of water, take a liquid in which the solid is insoluble and it sinks in the liquid.
Then, R.D. = (Weight of solid in air/Loss of weight of solid in liquid) x R.D. of the liquid
Solution 13S.
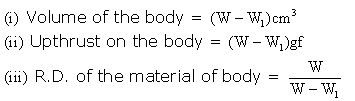
Solution 14S.
Experimental determination of R.D. of a solid lighter than water (such as cork):
- Take a sinker (i.e. a piece of metal or stone).
- Place a beaker nearly two-third filled with water on a wooden bridge kept over the left pan of a physical balance.
- Suspend the sinker with a thread from the hook of the left pan of balance so that it is completely immersed in water (as shown in the figure below). Find the weight W1 of the sinker in water.
- Tie the given solid (say, a cork) in the middle of a thread, and then measure the weight W2 of a solid in the air along with the sinker in water.
- Tie the cork with the sinker and immerse both of them completely in water of beaker and measure the weight W3 of the solid and sinker both in water.
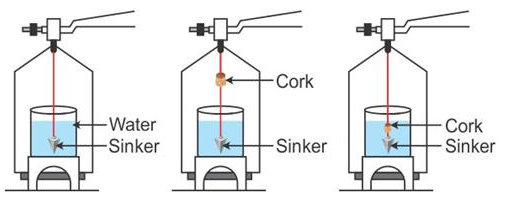
Observations:
Weight of the sinker in water = W1gf
Weight of the sinker in water and cork in air = W2gf
Weight of sinker and cork together in water = W3gf
Calculations:
Weight of cork in air = (W2 – W1) gf
Weight of cork in water = (W3 – W1) gf
Loss in weight of the cork in water = Weight of cork in air Weight of cork in water.
= [(W2 – W1) – (W3 – W1)] gf
= (W2 – W3) gf
R.D. of cork = Weight of cork in air/Loss of weight of cork in water
Or, R.D. of cork = (W2 – W1)/(W2 – W3).
Solution 15S.
The weight of the sinker and cork combined, in water will be less than the weight of the sinker alone in water because the upthrust due to water on cork (when completely immersed) is more than the weight of cork itself.
Solution 1M.
Water
Solution 2M.
No unit.
Solution 3M.
1 g cm-3
Solution 1N.
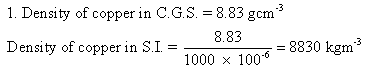
Solution 2N.

Solution 3N.
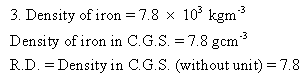
Solution 4N.

Solution 5N.
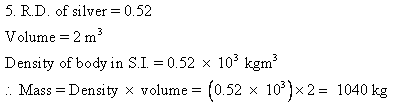
Solution 6N.
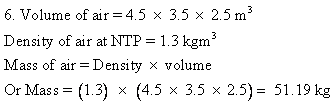
Solution 7N.
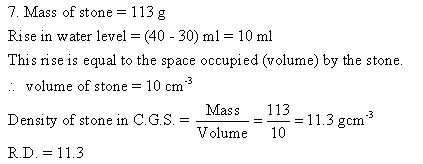
Solution 8N.

Solution 9N.

Solution 10N.
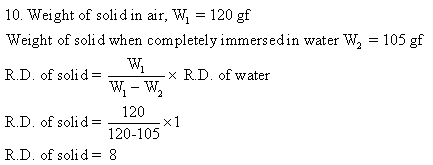
Solution 11N.
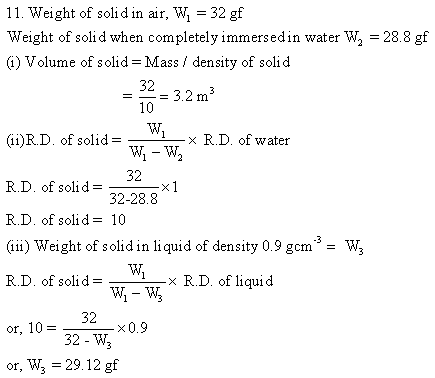
Solution 12N.
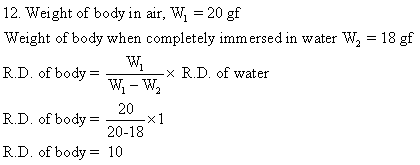
Solution 13N.
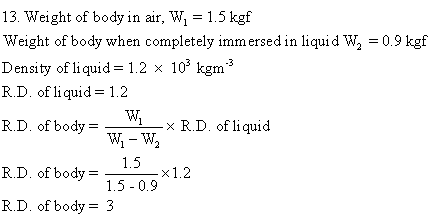
Solution 14N.

Solution 15N.

Solution 16N.
a. The mass of stone is 15.1 g. Hence, its weight in air will be Wa = 15.1 gf
b. When stone is immersed in water its weight becomes 9.7 gf. So, the upthrust on the stone is 15.1 – 9.7 = 5.4 gf, Since the density of water is 1 g cm-3, the volume of stone is 5.4 cm3.
c. Weight of stone in liquid is Wl = 10.9 gf
Weight of stone in water is Ww = 9.7 gf
Therefore, the relative density of stone is
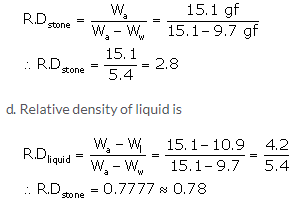
Exercise 5(C)
Solution 1S.
According to the principle of floatation, the weight of a floating body is equal to the weight of the liquid displaced by its submerged part.
Solution 2S.
(i) Two forces acting on the body are as listed below:
(a) Weight of the body (downwards)
(b) Upthrust of the liquid (upwards)
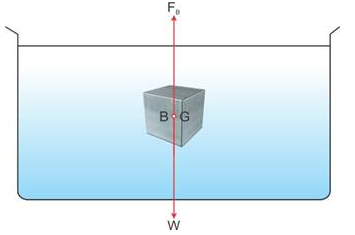
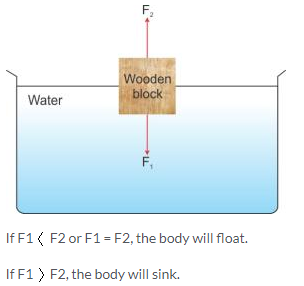
(ii) If the weight of the body is greater than the upthrust acting on it, the body will sink
If the weight of the body is equal to or less than the upthrust acting on it, the body will float.
(iii) (a) The net force acting on the body when it sinks is body’s own weight.
(b) The net force acting on the body when it floats is the upthrust due to the liquid.
Solution 3S.
The reading on the spring balance will be zero because wood floats on water and while floating the apparent weight = 0.
Solution 4S.
(a) The ball will float because the density of ball (i.e. iron) is less than the density of mercury.
(b) While floating, the apparent weight = 0.
Solution 5S.
The body will float if its density is less than or equal to the density of the liquid ρS ≤ ρL.
The body will sink if its density is greater than the density of the liquid ρS > ρL.
Solution 6S.
Density of iron is less than the density of mercury; hence, an iron nail floats in mercury and density of iron is more than the density of water; hence, an iron nail sinks in water.
Solution 7S.
(i) Weight of the floating body is equal to the upthrust.
(ii) While floating, the apparent weight is zero.
Solution 8S.
When the body is partially immersed, its centre of buoyancy will be below the centre of gravity of the block.
When the body is completely immersed, its centre of buoyancy will coincide the centre of gravity.
Solution 9S.
The upthrust on the body by each liquid is the same and equal to the weight of the body.
However, upthrust = Volume submerged × ρL × g,
For the liquid C, since the volume submerged is least so the density ρ3 must be maximum.
Solution 10S.
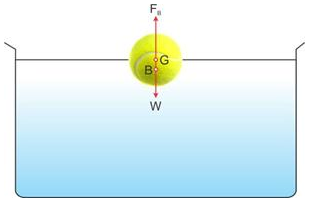
The forces acting are as listed below:
- Weight of the body acting downwards.
- Upthrust due to water acting upwards.
Weight of water displaced by the floating body = Weight of the body
Solution 11S.
Centre of buoyancy: It is the point through which the resultant of the buoyancy forces on a submerged body act; it coincides with the centre of gravity of the displaced liquid, if the body is completely immersed.
For a floating body with its part submerged in the liquid, the centre of buoyancy is at the centre of gravity of the submerged part of the body and it lies vertically below the centre of gravity of the entire body.
Solution 12S.
Observation : The balloon will sink.
Explanation : As air is pumped out from jar, the density of air in jar decreases, so the upthrust on balloon decreases. As weight of balloon exceeds the upthrust on it, it sinks.
Solution 13S.
(a) It will float with some part outside water.
Reason : On adding some salt to water, the density of water increases, so upthrust on a block of wood increases, and hence, the block rises up till the weight of salty water displaced by the submerged part of block becomes equal to the weight of the block.
(b) The block will sink.
Reason: On heating, the density of water decreases, so upthrust on the block decreases and the weight of block exceeds upthrust due to which it sinks.
Solution 14S.

Solution 15S.
Density of brine is more than the density of water. Hence, the upthrust exerted by brine is more than the upthrust exerted by water on ice. Therefore, floating ice is less submerged in brine.
Solution 16S.
(i) 1:1; The weight of the water displaced by the man in sea and river will be same and will be equal to his own weight.
(ii) He finds it easier to swim in the sea because the density of sea water is more than the density of river water. So his weight is balanced in sea water with a part of his body submerged in the water.
Solution 17S.
An iron nail sinks in water because density of iron is more than the density of water, so the weight of the nail is more than the upthrust of water on it.
On the other hand, ships are also made of iron, but they do not sink. This is because the ship is hollow and the empty space in it contains air, which makes its average density less than that of water. Therefore, even with a small portion of ship submerged in water, the weight of water displaced by the submerged part of ship becomes equal to the total weight of ship and it floats.
Solution 18S.
Due to the hollow and empty space in the ship, the average density of a ship is less than the density of water.
Solution 19S.
When a floating piece of ice melts into water, it contracts by the volume equal to the volume of ice pieces above the water surface while floating on it. Hence, the level of water does not change when ice floating on it melts.
Solution 20S.
Forces acting on the body are listed below:
- Weight of the body vertically downwards.
- Upthrust of water on body vertically upwards.
- Tension in thread vertically downwards.
Solution 21S.
A ship submerges more as it sails from sea water to river water.
Density of river water is less than the density of sea water. Hence, according to the law of floatation, to balance the weight of the ship, a greater volume of water is required to be displaced in river water of lower density.
Solution 22S.
(a) Icebergs are dangerous for ships as they may collide with them. Icebergs being lighter than water, float on water with a major part of their surfaces laying under the water surface and only a small part lies outside water. Thus, it becomes difficult for the driver of the ship to estimate the size of the iceberg.
(b) Density of a strong salt solution is more than the density of fresh water. Hence, the salt solution exerts a greater upthrust on the egg which balances the weight of the egg, so the egg floats in a strong salt solution but sinks in fresh water.
(c) Density of hydrogen is much less than the density of carbon dioxide. When a balloon is filled with hydrogen, the weight of the air displaced by an inflated balloon (i.e. upthrust) becomes more than the weight of a gas filled balloon, and hence, it rises. In case of a balloon filled with carbon dioxide, weight of the balloon becomes more than the upthrust of the air, and hence, it sinks to the floor.
(d) As a ship in harbor is unloaded, its weight decreases. As a result, it displaces less water, and the ship’s hull rises in water till the weight of the water displaced balances the weight of the unloaded ship.
(e) The reason is that the density of air decreases with altitude. Therefore, as the balloon gradually goes up, the weight of the displaced air (i.e. uphrust) decreases. It keeps on rising as long as the upthrust exceeds its weight. When upthrust becomes equal to its weight, it stops rising.
(f) Density of river water is less than the density of sea water. Hence, according to the law of floatation, to balance the weight of the ship, a great volume of water is required to be displaced in river water having a comparitively lower density.
Solution 1M.
W= FB
Solution 2M.
Zero
Solution 3M.
ρ1 > ρ2
Solution 1N.

Solution 2N.

Solution 3N.

Solution 4N.

Solution 5N.
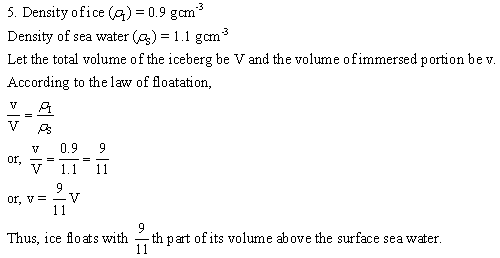
Solution 6N.

Solution 7N.

Solution 8N.

Solution 9N.

More Resources for Selina Concise Class 9 ICSE Solutions