ICSE Solutions for Class 10 Mathematics – Quadratic Equation
ICSE SolutionsSelina ICSE Solutions
Get ICSE Solutions for Class 10 Mathematics Chapter 6 Quadratic Equation for ICSE Board Examinations on APlusTopper.com. We provide step by step Solutions for ICSE Mathematics Class 10 Solutions Pdf. You can download the Class 10 Maths ICSE Textbook Solutions with Free PDF download option.
Download Formulae Handbook For ICSE Class 9 and 10


Formulae
- The standard form of a quadratic equation is ax2 + bx + c = 0, where a, b and c are all real numbers and a ≠ 0.
e.g., equation 4x2 + 5x – 6 = 0 is a quadratic equation in standard form. - Every quadratic equation gives two values of the unknown variable and these values are called roots of the equation.
- Zero Product Rule: Whenever the product of two expressions is zero; at least one of the expressions is zero.
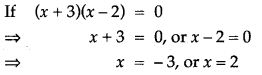
- Solving quadratic equations using the formula:
The roots of the quadratic equation ax2 + bx + c = 0; where a ≠ 0 can be obtained by using the formula:
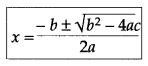
- To examine the nature of the roots:
Examining the roots of a quadratic equation means to see the type of its roots i.e., whether they are real or imaginary, rational or irrational, equal or unequal.
The nature of the roots of a quadratic equation depends entirely on the value of its discriminant b2 – 4ac.
Case I: If a, b and c are real numbers and a ≠ 0, then discriminant:
(i) b2 – 4ac = 0 ⇒ the roots are real and equal.
(ii) b2 – 4a c > 0 ⇒ the roots are real and unequal.
(iii) b2 – 4ac < 0 ⇒ the roots are imaginary (not real).
Case II: If a, b and c are rational numbers and a ≠ 0, then discriminant.
(i) b2 – 4ac = 0 ⇒ the roots are rational and equal.
(ii) b2 – 4ac > 0 and b2 – 4ac is a perfect square ⇒ the roots are rational and unequal.
(iii) b2 – 4ac > 0 and b2 – 4ac is not a perfect square ⇒ the roots are irrational and unequal.
(iv) b2 – 4ac < 0 ⇒ the roots are imaginary. - Sum and product of the roots: If a and P are the roots of quadratic equation ax2 + bx + c = 0 then

- To form a quadratic equation with given roots: Let α, β be the roots of the required quadratic equation, then
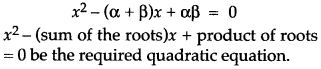
Determine the Following
Question 1. Which of the following are quadratic equation:
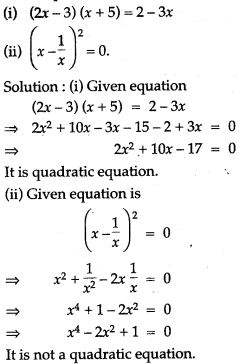
Question 2. Determine, if 3 is a root of the given equation

Question 3. Examine whether the equation 5x² -6x + 7 = 2x² – 4x + 5 can be put in the form of a quadratic equation.
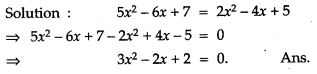
Question 4. Find if x = – 1 is a root of the equation 2x² – 3x + 1 = 0.

Question 6. 48x² – 13x -1 = 0
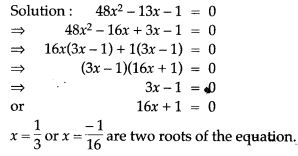


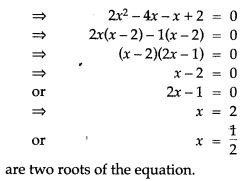


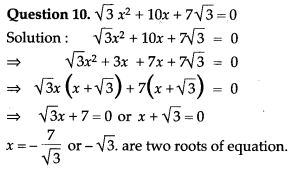
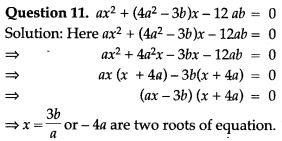
Question 12. Without solving the following quadratic equation, find the value of ‘p’ for which the given equation has real and equal roots: x² + (p – 3) x + p = 0
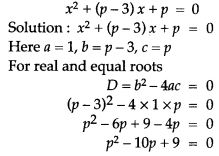
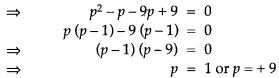
Question 13. Find the value of k for which the following equation has equal roots:

Question 14. If one root of the equation 2x² – px + 4 = 0 is 2, find the other root. Also find the value of p.

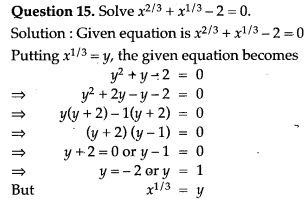
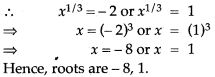
Question 16. The sum of two numbers is 15. If the sum of reciprocals is 3/10, find the numbers.

Question 17. Find two consecutive natural numbers whose squares have the sum 221.

Question 18. The sum of the squares of three consecutive natural numbers is 110. Determine the numbers.
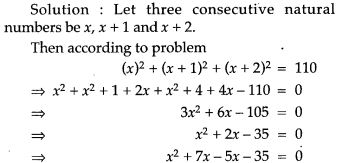
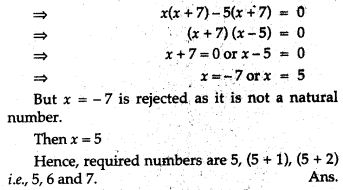
Question 19. If an integer is added to its square the sum is 90. Find the integer with the help of a quadratic equation.

Question 20. Find two consecutive positive even integers whose squares have the sum 340.
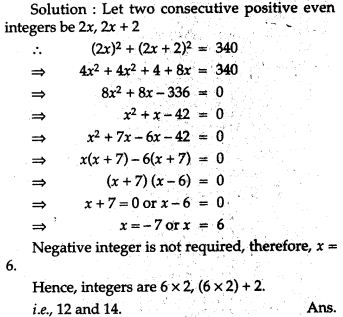
Question 21. Divide 29 into two parts so that the sum of the square of the parts is 425.
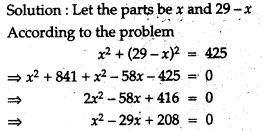
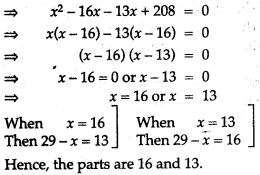
Question 22. In a two digit number, the unit’s digit is twice the ten’s digit. If 27 is added to the number, the digit interchange their places. Find the number.

Question 23. A two digit positive number is such that the product of its digits is 6. If 9 is added to the number, the digits interchange their places. Find the number.

Question 24. Five years ago, a woman’s age was the square of her son’s age. Ten years later her age will be twice that of her son’s age. Find:
(i) The age of the son five years ago.
(ii) The present age of the woman.

Question 25. The length of verandah is 3m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x, breadth of the verandah write an equation in ‘x’ that represents the above statement.
(ii) Solve the equation obtained in above and hence find the dimension of verandah.
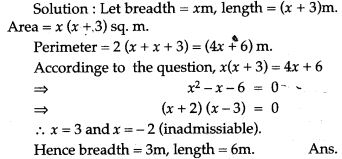
Question 26. A two digit number is such that the product of its digit is 14. When 45 is added to the number, then the digit interchange their places. Find the number.

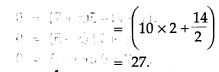
Question 27. In each of the following determine the; value of k for which the given value is a solution of the equation:

Question 28. If x = 2 and x = 3 are roots of the equation 3x² – 2kx + 2m = 0. Find the values of k and m.

Question 29. Solve the following equation and give your answer up to two decimal places:

Question 30. Determine whether the given values of x is the solution of the given quadratic equation below:
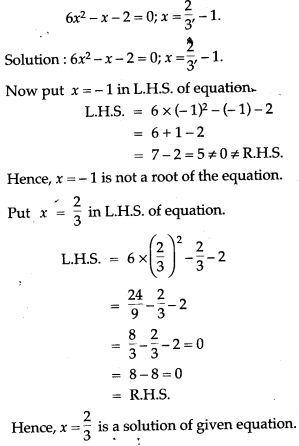


Question 32. Solve using the quadratic formula x² – 4x + 1 = 0

Question 33. Solve the quadratic equation:
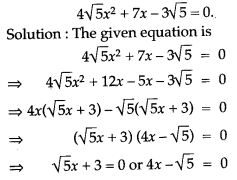
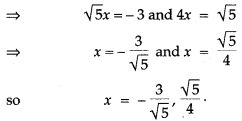
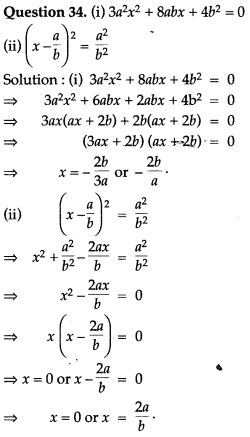

Question 36. Form the quadratic equation whose roots are:

Question 37. Find the value of k for which the given equation has real roots:

Question 38. Without actually determining the roots comment upon the nature of the roots of each of the following equations:

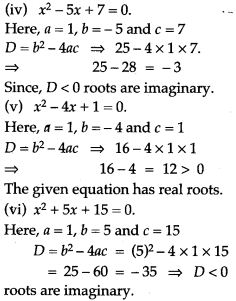
Question 39. Solve the equation 3x² – x – 7 = 0 and give your answer correct to two decimal places.
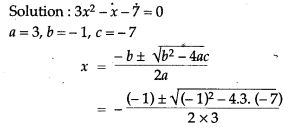
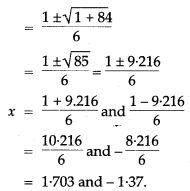
Question 40. Solve for x using the quadratic formula. Write your answer correct to two significant figures (x -1)² – 3x + 4 = 0.

Question 41. Without solving the following quadratic equation, find the value of ‘m’ for which the given equation has real and equal roots.
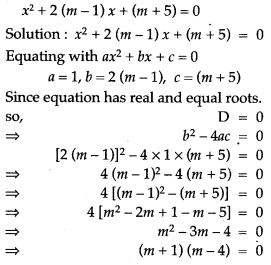

Question 42. Solve the following by reducing them to quadratic equations:


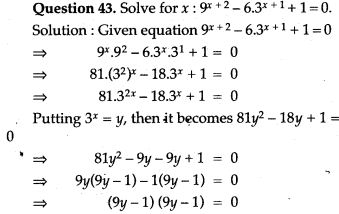
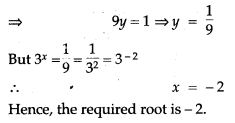
Question 44. Solve for x:
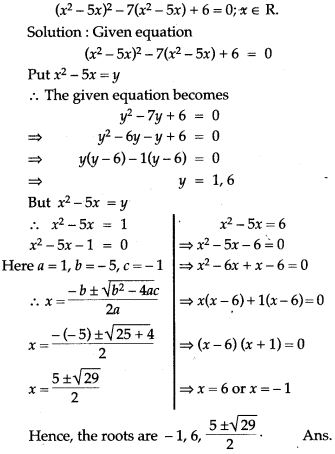
Question 45. Solve the following equation by reducing it to quadratic equation:

Question 46. Solve:

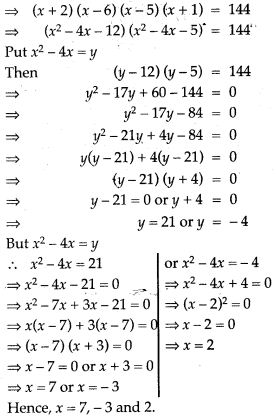
Question 47. A two digit number is such that the product of the digits is 12. When 36 is added to this number the digits interchange their places. Determine the number.

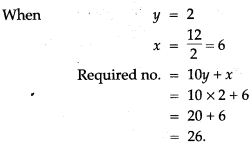
Question 48. The side (in cm) of a triangle containing the right angle are 5x and 3x – 1. If the area of the triangle is 60 cm². Find the sides of the triangle.

Question 49. Rs. 480 is divided equally among ‘x’ children. If the number of children were 20 more then each would have got Rs. 12 less. Find ‘x’.


Question 50. By increasing the speed of a car by 10 km/hr, the time of journey for a distance of 72 km. is reduced by 36 minutes. Find the original speed of the car.
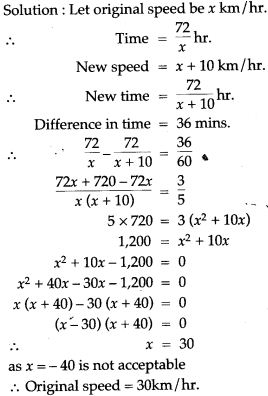
Question 51. A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/hr more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car.


Question 52. The speed of an express train is x km/hr arid the speed of an ordinary train is 12 km/hr less than that of the express train. If the ordinary train takes one hour longer than the express train to cover a distance of 240 km, find the speed of the express train.

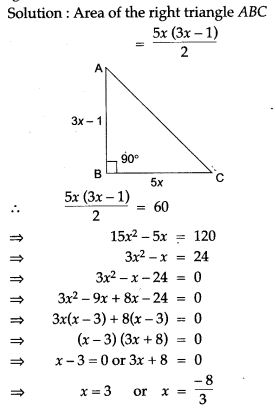
Question 53. Some students planned a picnic. The budget for the food was Rs. 480. As eight of them failed to join the party, the cost of the food for each member increased by Rs. 10. Find how many students went for the picnic.
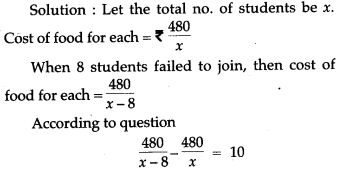
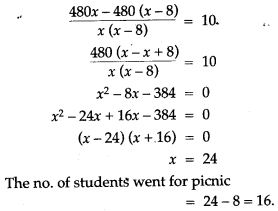
Question 54. Two pipes flowing together can fill a cistern in 6 minutes. If one pipe takes 5 minutes more than the other to fill the cistern, find the time in which each pipe would fill the cistern.

Question 55. One fourth of a herd of camels was seen in the forest. Twice the square root of the herd had gone to mountains and the remaining 15 camels were seen on the bank of a river. Find the total number of camels.

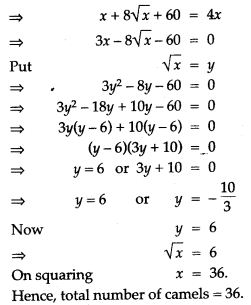
Question 56. An aeroplane travelled a distance of 400 km at an average speed of x km/hr. On the return journey the speed was increased by 40 km/hr. Write down the expression for the time taken for
(i) The outward journey (ii) the return Journey. If the return journey took 30 minutes less than the onward journey write down an equation in x and find its value.

Question 57. Car A travels x km for every litre of petrol, while car B travels (x + 5) km for every litre of petrol.
(i) Write down the number of litres of petrol used by car A and car B in covering a distance of 400 km.
(ii) If car A use 4 litre of petrol more than car B in covering the 400 km, write down and equation in x and solve it to determine the number of litre of petrol used by car B for the journey.
Solution: Given Distance = 400 km


Question 58. A shopkeeper purchases a certain number of books for Rs. 960. If the cost per book was Rs. 8 less, the number of books that could be purchased for Rs. 960 would be 4 more. Write an equation, taking the original cost of each book to be Rs. x, and Solve it to find the original cost of the books.

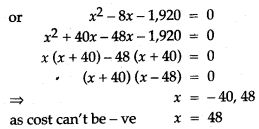
Question 59. Two pipes running together can 1 fill a cistern in 11 1/9 minutes. If one pipe takes 5 minutes more than the other to fill the cistern find the time when each pipe would fill the cistern.

Question 60. In each of the following find the values of k of which the given value is a solution of the given equation:


Question 61. Solve the following quadratic equation by factorisation:

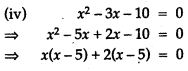

Question 62. Solve the following quadratic equation by factorisation method:
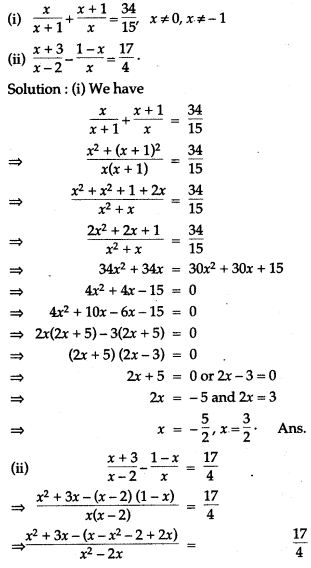
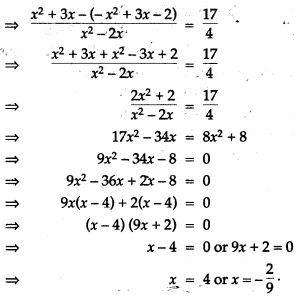
Question 63. Solve the following quadratic equation:
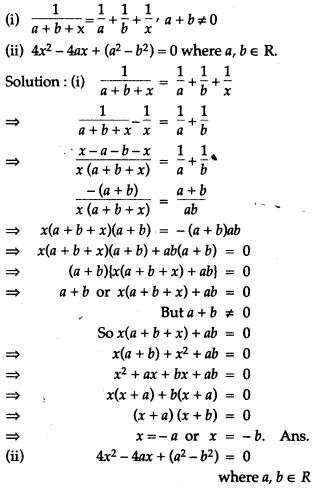
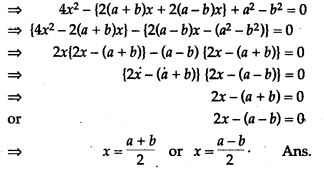
Question 64. Determine whether the given quadratic equations have equal roots and if so, find the roots:
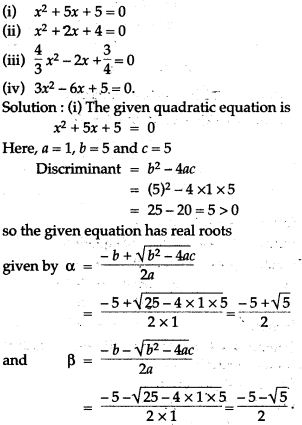

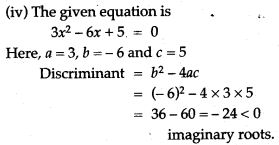
Question 65. Find the value of k so that sum of the roots of the quadratic equation is equal to the product of the roots:


Question 66. Find the values of k so that the sum of tire roots of the quadratic equation is equal to the product of the roots in each of the following:
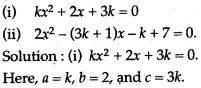

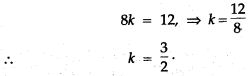
Question 67. Solve the following by reducing them to quadratic equations:
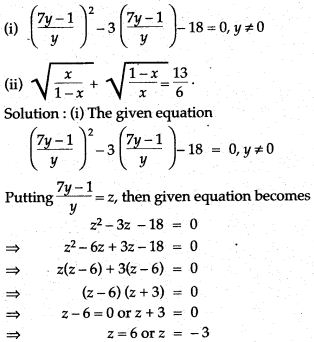


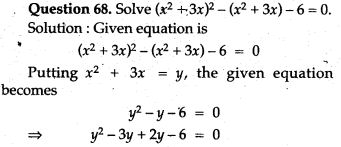
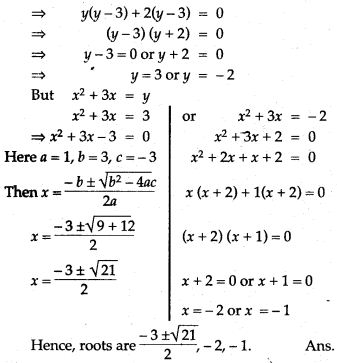
Question 69. Solve the following by reducing them to quadratic form:
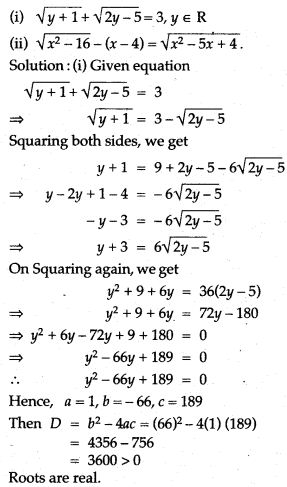
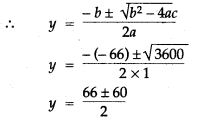
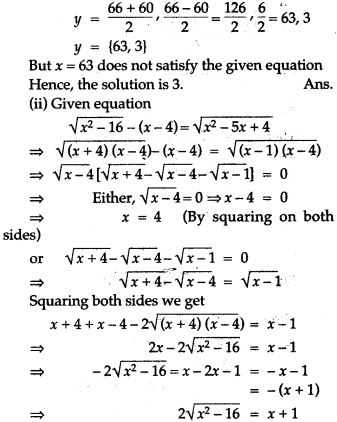
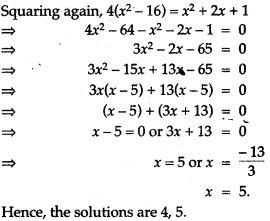
Question 70. Solve: x(x + 1) (x + 3) (x + 4) = 180.
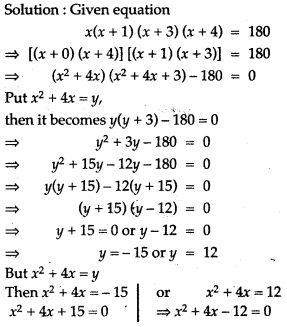
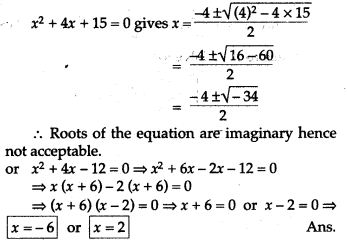
Question 71. Solve the equation:
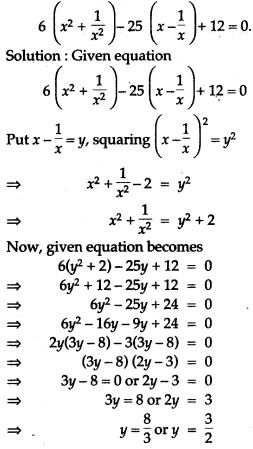
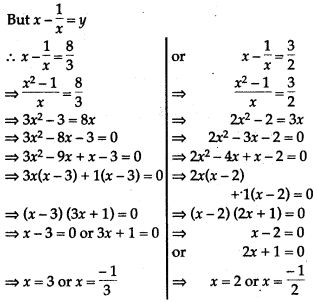
![]()
Question 72. Solve for x:
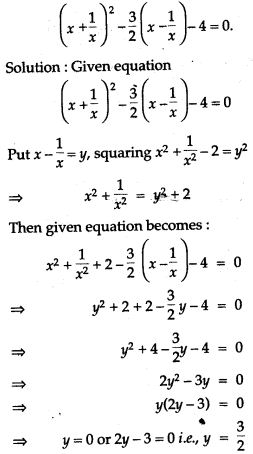
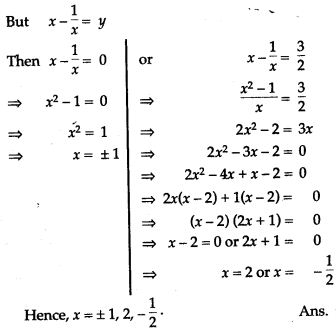
Question 73. Solve the equation
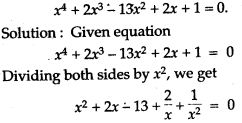
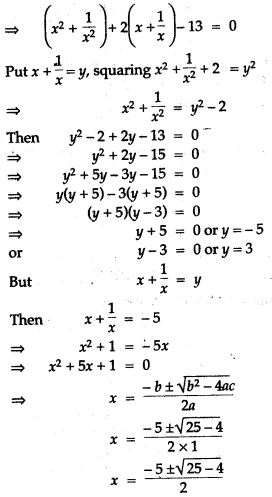

Prove the Following
Question 1. Given that one root of the quadratic equation ax2 + bx + c = 0 is three times the other, show that 3b2 – 16ac.

Question 2. If one root of the quadratic equation ax2 + bx + c = 0 is double the other, prove that 2b2 = 9 ac.

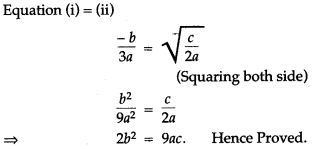
Question 3. If the ratio of the roots of the equation

Question 4. In each of the following determine whether the given values are solutions of the equation or not.
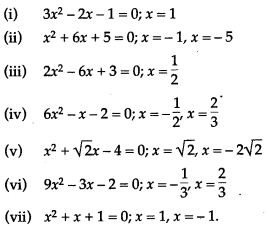

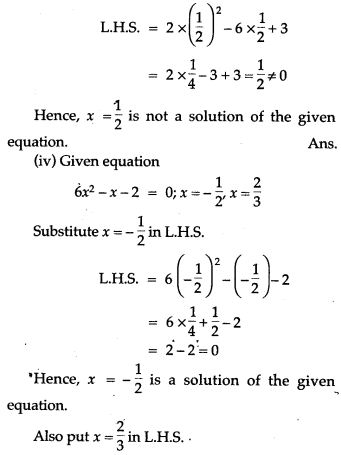


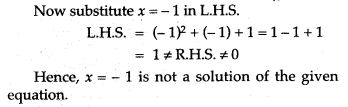
Question 5. In each of the following, determine whether the given values are solution of the given equation or not:






Question 7. Show, that a, b, c, d are in proportion if:
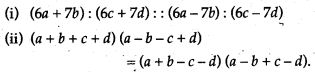

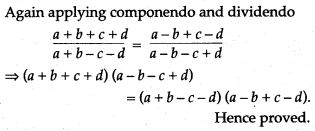

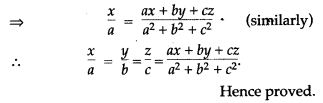




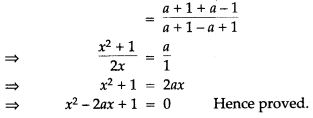
Concept Based Questions
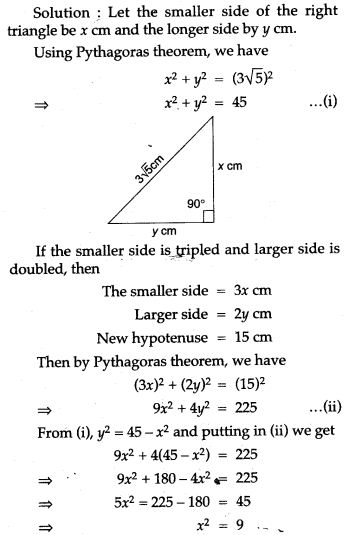
Question 1. The hypotenuse of a right angled triangle is 3√5. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be 15 cm. Find the length of each side.

For More Resources