ICSE Solutions for Class 10 Mathematics – Locus and Constructions
ICSE SolutionsSelina ICSE Solutions
Get ICSE Solutions for Class 10 Mathematics Chapter 14 Loci (Locus and its Constructions) for ICSE Board Examinations on APlusTopper.com. We provide step by step Solutions for ICSE Mathematics Class 10 Solutions Pdf. You can download the Class 10 Maths ICSE Textbook Solutions with Free PDF download option.
Download Formulae Handbook For ICSE Class 9 and 10
Formulae
Theorems on Locus:
(a) The locus of a point equidistant from a fixed point is a circle with the fixed point as centre.
(b) The locus of a point equidistant from two interacting lines is the bisector of the angles between the lines.
(c) The locus of a point equidistant from two given points is the perpendicular bisector of the line joining the points.
Prove the Following
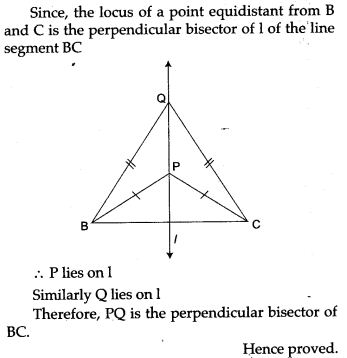
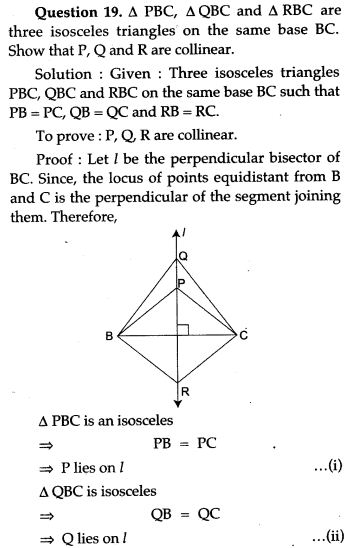
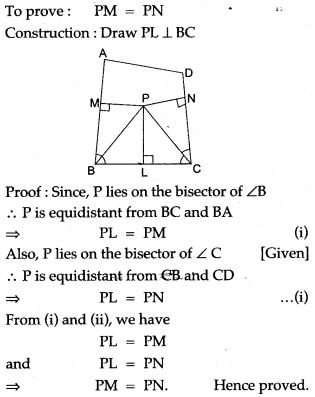
Question 1. The bisector of ∠ B and ∠C of a quadrilateral ABCD intersect in P, show that P is equidistant from the opposite sides AB and CD.
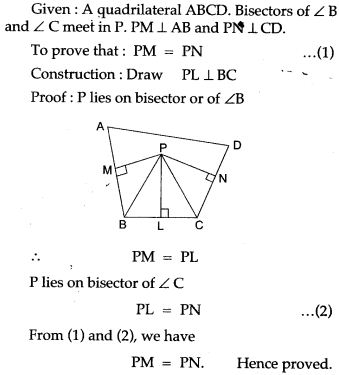
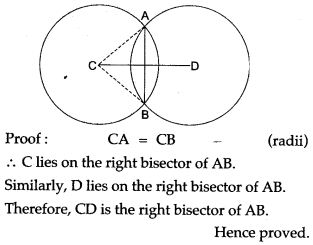
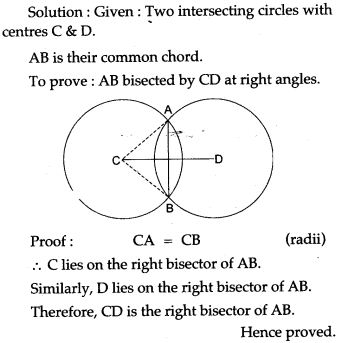
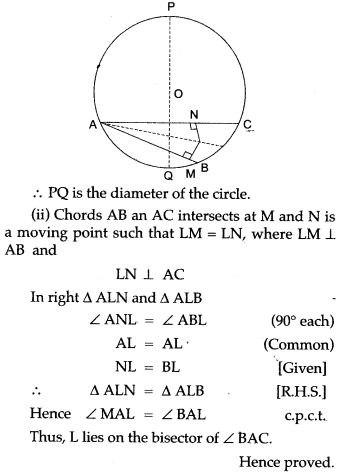
Question 2. Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.


Question 4. In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.
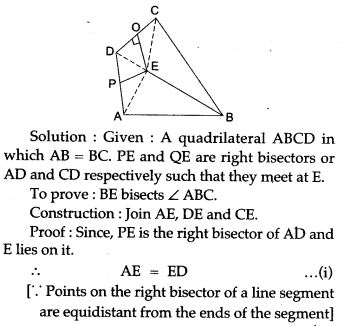

Figure Based Questions

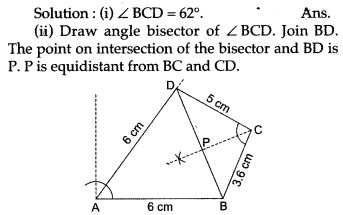
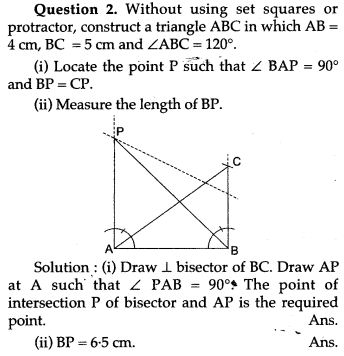
Question 3. State and draw the locus of a swimmer maintaining the same distance from a lighthouse.

Question 4. State and draw the locus of a point equidistant from two given parallel lines.

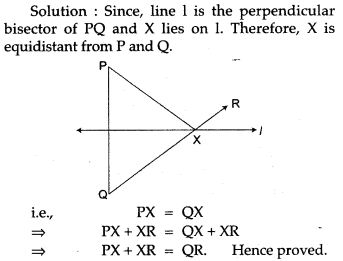
Question 5. l is the perpendicular bisector of line segment PQ and R is a point on the same side of l as P. The segment QR intersects l at X. Prove that PX + XR = QR.
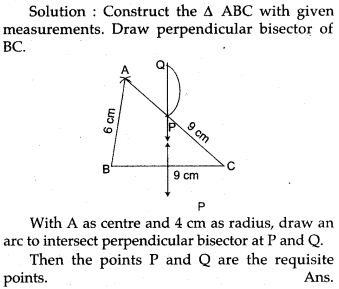
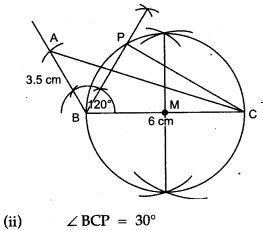
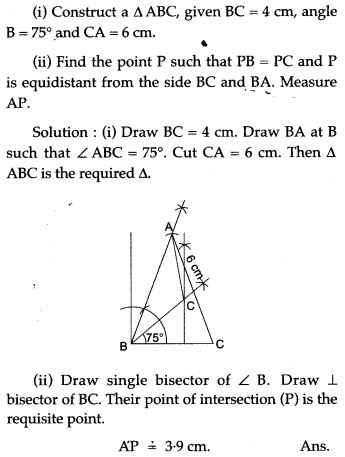
Question 6. Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
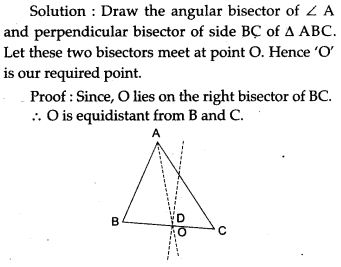
Question 7. Given a Δ ABC with unequal sides. Find a point which is equidistant from B and C as well as from AB and AC.

Question 8. Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
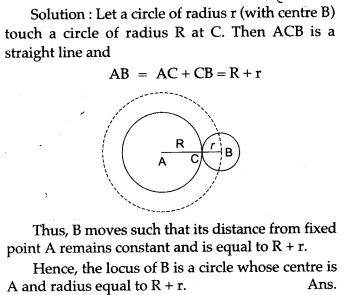
Question 9. Find the locus of the centre of a circle of radius r touching externally a circle of radius R.


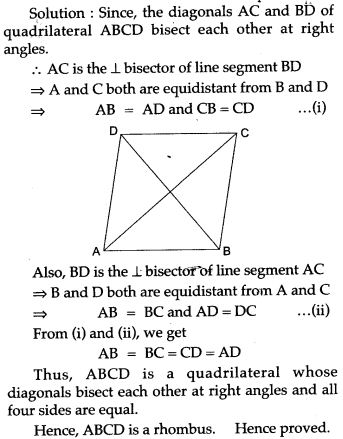
Question 12. The diagonals of a quadrilateral bisect each other at right angles. Show that the quadrilateral is a rhombus.
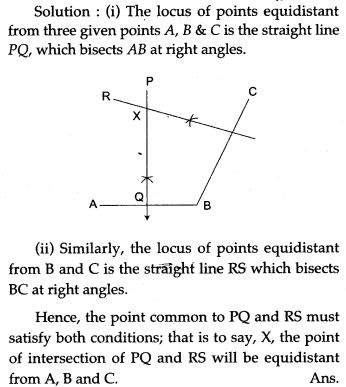
Question 13. What is the locus of points which are equidistant from the given non-collinear point A, B and C? Justify your answer.
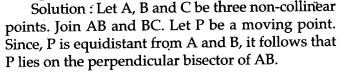
Question 14. Find the locus of points which are equidistant from three non-collinear points.

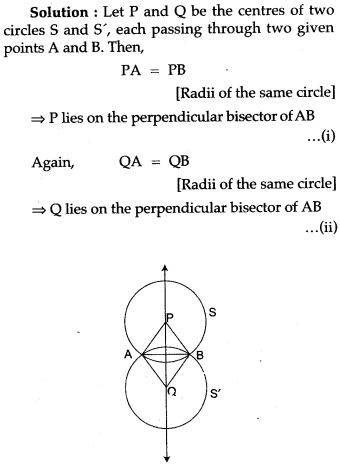
Question 15. Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.

From (i) and (ii), it follows that P and Q both lies on the perpendicular bisector of AB.
Hence, the locus of the centres of all the circles passing through A and B is the perpendicular bisector of AB.
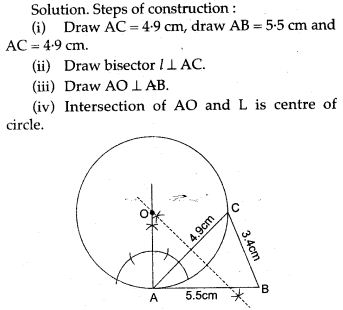
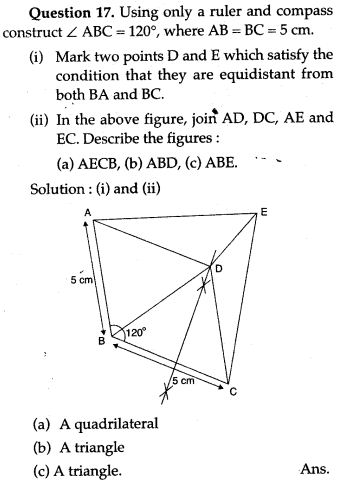
Question 16. Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
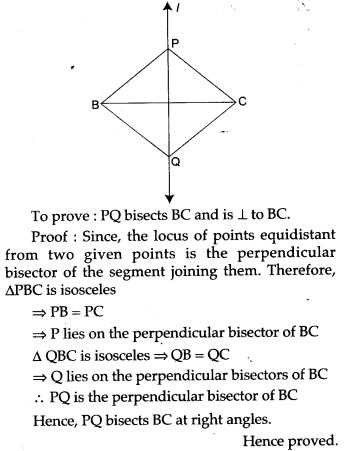
Question 18. ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.


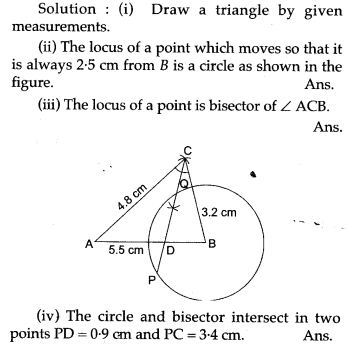
Question 20. Without using set squares or protractor construct:
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Question 21. Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length f 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.

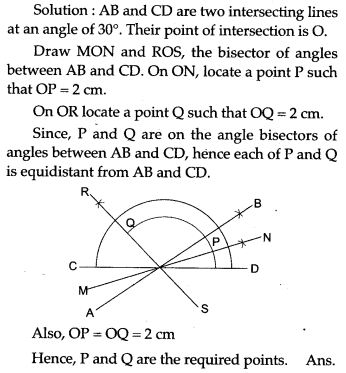
Question 22. Draw two intersecting lines to include an angle of 30°. Use ruler and compass to locate points, which are equidistant from these lines and also 2 cm away from these points of intersection. How many such points exist ?
Question 23. How will you find a point equidistant from three given points A, B, C which are not in the same straight line?
Question 24. Without using set squares or protractor.


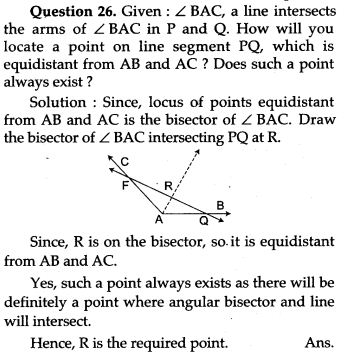

Question 28. Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
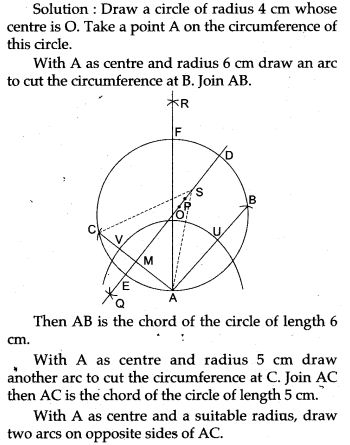
With C as centre and the same radius, draw two arcs on opposite sides of AC to intersect the former arcs at P and Q.
Join PQ and produce to cut the circle at D and E.
Join DE. Then chord DE is the locus of points inside the circle that Ls equidistant from A and C.
As chord DE passes through (he centre O of the circle, it is a diameter. To prove the construction take any point S inside the circle on DE.
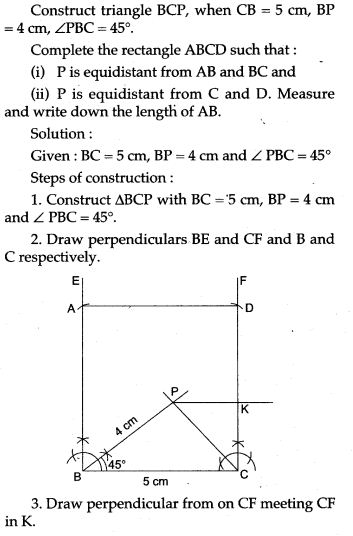
Question 29. Use ruler and compasses only for the following questions:

![]()
Question 30. Ruler and compass only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct Δ ABC, in which BC = 8 cm, AB = 5 cm, ∠ ABC = 60°.

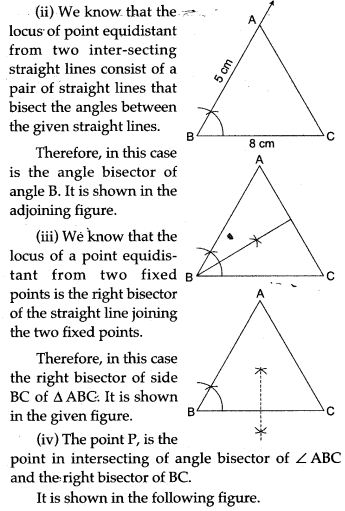
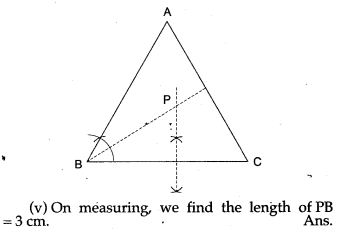
Question 31. Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
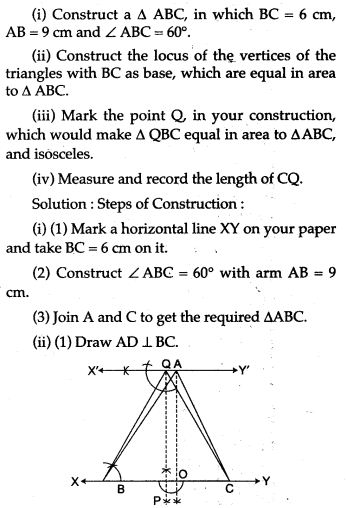


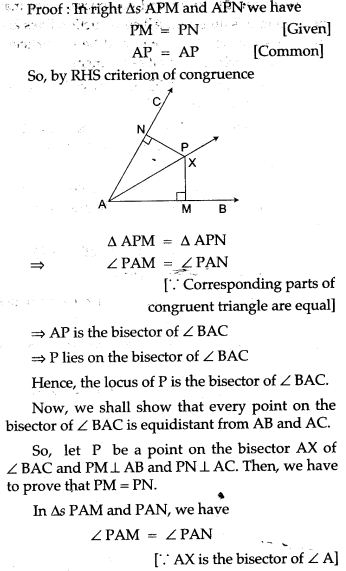

Graphical Depiction
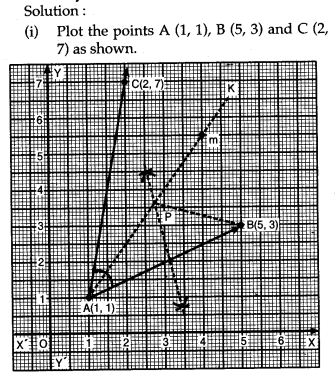
Question 1. Use graph paper for this question. Take 2 cm = 1 unit on both axis.
(i) Plot the points A (1, 1), B (5, 3) and C (2, 7);
(ii) Construct the locus of points equidistant from A and B;
(iii) Construct the locus of points equidistant from AB and AC;
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC;
(v) Measure and record the length PA in cm.

For More Resources