Graphical Method Of Solving Linear Equations In Two Variables
Let the system of pair of linear equations be
a1x + b1y = c1 ….(1)
a2x + b2y = c2 ….(2)
We know that given two lines in a plane, only one of the following three possibilities can happen –
(i) The two lines will intersect at one point.
(ii) The two lines will not intersect, however far they are extended, i.e., they are parallel.
(iii) The two lines are coincident lines.

Types Of Solutions:
There are three types of solutions
- Unique solution.
- Infinitely many solutions
- No solution.
Read More:
- What is a Linear Equation
- Linear Equations In Two Variables
- Linear Equations In One Variable
- RS Aggarwal Class 10 Solutions Linear Equations In Two Variables
- RS Aggarwal Class 9 Solutions Linear Equations In Two Variables
- RS Aggarwal Class 8 Solutions Linear Equations
- RS Aggarwal Class 7 Solutions Linear Equations in One Variable
- RS Aggarwal Class 6 Solutions Linear Equation In One Variable
(A) Consistent: If a system of simultaneous linear equations has at least one solution then the system is said to be consistent.
(i) Consistent equations with unique solution: The graphs of two equations intersect at a unique point.
For Example Consider
x + 2y = 4
7x + 4y = 18

The graphs (lines) of these equations intersect each other at the point (2, 1) i.e., x = 2, y = 1.
Hence, the equations are consistent with unique solution.
(ii) Consistent equations with infinitely many solutions: The graphs (lines) of the two equations will be coincident.
For Example Consider 2x + 4y = 9 ⇒ 3x + 6y = 27/2

The graphs of the above equations coincide. Coordinates of every point on the lines are the solutions of the equations. Hence, the given equations are consistent with infinitely many solutions.
(B) Inconsistent Equation: If a system of simultaneous linear equations has no solution, then the system is said to be inconsistent.
No Solution: The graph (lines) of the two equations are parallel.
For Example Consider
4x + 2y = 10
6x + 3y = 6

The graphs (lines) of the given equations are parallel. They will never meet at a point. So, there is no solution. Hence, the equations are inconsistent.



From the table above you can observe that if the line a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are

Graphical Method Examples
https://www.youtube.com/watch?v=mo8qxxrRce4
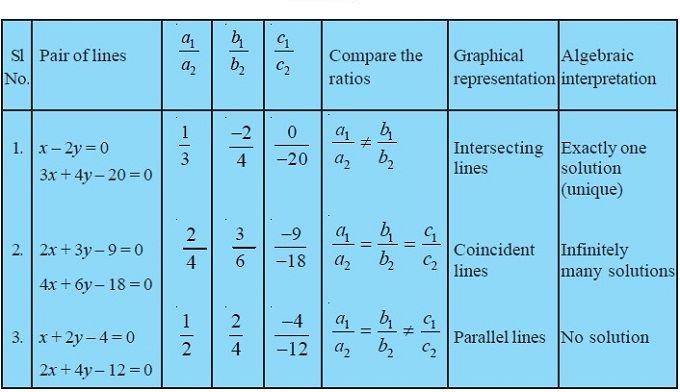
Example 1: The path of highway number 1 is given by the equation x + y = 7 and the highway number 2 is given by the equation 5x + 2y = 20. Represent these equations geometrically.
Sol. We have, x + y = 7
⇒ y = 7 – x ….(1)
In tabular form
| x | 1 | 4 |
| y | 6 | 3 |
| Points | A | B |
and 5x + 2y = 20
⇒ y = \(\frac { 20-5x }{ 2 }\) ….(2)
In tabular form
| x | 2 | 4 |
| y | 5 | 0 |
| Points | C | D |
Plot the points A (1, 6), B(4, 3) and join them to form a line AB.
Similarly, plot the points C(2, 5). D (4, 0) and join them to get a line CD. Clearly, the two lines intersect at the point C. Now, every point on the line AB gives us a solution of equation (1). Every point on CD gives us a solution of equation (2).
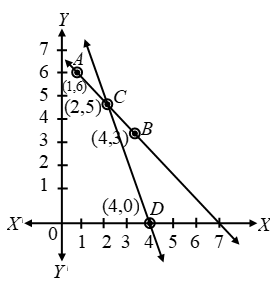
Example 2: A father tells his daughter, “ Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Represent this situation algebraically and graphically.
Sol. Let the present age of father be x years and that of daughter = y years
Seven years ago father’s age = (x – 7) years
Seven years ago daughter’s age = (y – 7) years
According to the problem
(x – 7) = 7(y – 7) or x – 7y = – 42 ….(1)
After 3 years father’s age = (x + 3) years
After 3 years daughter’s age = (y + 3) years
According to the condition given in the question
x + 3 = 3(y + 3) or x – 3y = 6 ….(2)
x – 7y = –42 ⇒ \(y=\frac { x+42 }{ 7 }\)
| x | 0 | 7 | 14 |
| y | 6 | 7 | 8 |
| Points | A | B | C |
x – 3y = 6 ⇒ \(y=\frac { x-6 }{ 3 }\)
| x | 6 | 12 | 18 |
| y | 0 | 2 | 4 |
| Points | D | E | F |
Plot the points A(0, 6), B(7, 7), C(14, 8) and join them to get a straight line ABC. Similarly plot the points D(6, 0), E(12, 2) and F(18, 4) and join them to get a straight line DEF.
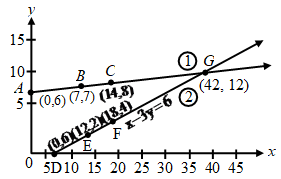
Example 3: 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Sol. Let the number of boys be x and the number of girls be y.
Then the equations formed are
x + y = 10 ….(1)
and y = x + 4 ….(2)
Let us draw the graphs of equations (1) and (2) by finding two solutions for each of the equations. The
solutions of the equations are given.
x + y = 10 ⇒ y = 10 – x
| x | 0 | 8 |
| y | 10 | 2 |
| Points | A | B |
y = x + 4
| x | 0 | 1 | 3 |
| y | 4 | 5 | 7 |
| Points | C | D | E |
Plotting these points we draw the lines AB and CE passing through them to represent the equations. The two lines AB and Ce intersect at the point E (3, 7). So, x = 3 and y = 7 is the required solution of the pair of linear equations.
i.e. Number of boys = 3
Number of girls = 7.
Verification:
Putting x = 3 and y = 7 in (1), we get
L.H.S. = 3 + 7 = 10 = R.H.S., (1) is verified.
Putting x = 3 and y = 7 in (2), we get
7 = 3 + 4 = 7, (2) is verified.
Hence, both the equations are satisfied.
Example 4: Half the perimeter of a garden, whose length is 4 more than its width is 36m. Find the dimensions of the garden.
Sol. Let the length of the garden be x and width of the garden be y.
Then the equation formed are
x = y + 4 ….(1)
Half perimeter = 36
x + y = 36 ….(2)
y = x – 4
| x | 0 | 4 |
| y | -4 | 0 |
| Points | A | B |
y = 36 – x
| x | 10 | 20 |
| y | 26 | 16 |
| Points | C | D |
Plotting these points we draw the lines AB and CD passing through them to represent the equations.
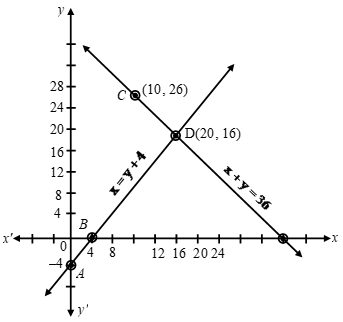
The two lines AB and CD intersect at the point (20, 16), So, x = 20 and y = 16 is the required solution of the pair of linear equations i.e. length of the garden is 20 m and width of the garden is 16 m.
Verification:
Putting x = 20 and y = 16 in (1). We get
20 = 16 + 4 = 20, (1) is verified.
Putting x = 20 and y = 16 in (2). we get
20 + 16 = 36
36 = 36, (2) is verified.
Hence, both the equations are satisfied.
Example 5: Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Sol. Pair of linear equations are:
x – y + 1 = 0 ….(1)
3x + 2y – 12 = 0 ….(2)
x – y + 1 = 0 ⇒ y = x + 1
| x | 0 | 4 |
| y | 1 | 5 |
| Points | A | B |
3x + 2y – 12 = 0 ⇒ y = \(\frac { 12-3x }{ 2 }\)
| x | 0 | 2 |
| y | 6 | 3 |
| Points | C | D |
Plot the points A(0, 1), B(4, 5) and join them to get a line AB. Similarly, plot the points C(0, 6), D(2, 3) and join them to form a line CD.
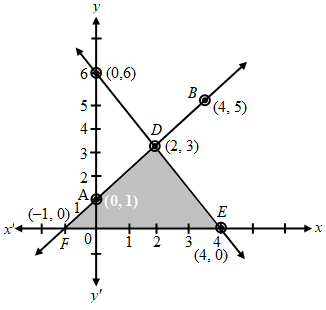
Clearly, the two lines intersect each other at the point D(2, 3). Hence x = 2 and y = 3 is the solution of the
given pair of equations.
The line CD cuts the x-axis at the point
E (4, 0) and the line AB cuts the x-axis at the point F(–1, 0).
Hence, the coordinates of the vertices of the triangle are; D(2, 3), E(4, 0), F(–1, 0).
Verification:
Both the equations (1) and (2) are satisfied by x = 2 and y = 3. Hence, Verified.
Example 6: Show graphically that the system of equations
x – 4y + 14 = 0; 3x + 2y – 14 = 0 is consistent with unique solution.
Sol. The given system of equations is
x – 4y + 14 = 0 ….(1)
3x + 2y – 14 = 0 ….(2)
x – 4y + 14 = 0 ⇒ y = \(\frac { x + 14 }{ 4 }\)
| x | 6 | -2 |
| y | 5 | 3 |
| Points | A | B |
3x + 2y – 14 = 0 ⇒ y = \(\frac { -3x + 14 }{ 2 }\)
| x | 0 | 4 |
| y | 7 | 1 |
| Points | C | D |
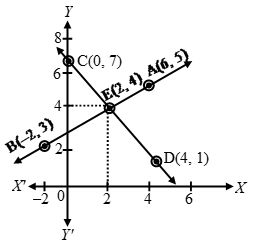
The given equations representing two lines, intersect each other at a unique point (2, 4). Hence, the equations are consistent with unique solution.
Example 7: Show graphically that the system of equations
2x + 5y = 16; \(3x+\frac { 15 }{ 2 }=24\) has infinitely many solutions.
Sol. The given system of equations is
2x + 5y = 16 ….(1)
\(3x+\frac { 15 }{ 2 }=24\) ….(2)
2x + 5y = 16 ⇒ y = \(\frac { 16-2x }{ 5 }\)
| x | -2 | 3 |
| y | 4 | 2 |
| Points | A | B |
\(3x+\frac { 15 }{ 2 }=24\) ⇒ y = \(\frac { 48-6x }{ 15 }\)
| x | 1/2 | 11/2 |
| y | 3 | 1 |
| Points | C | D |
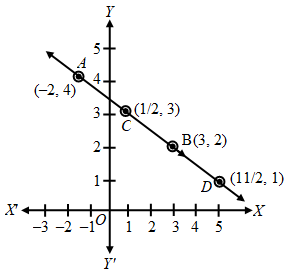
The lines of two equations are coincident. Coordinates of every point on this line are the solution.
Hence, the given equations are consistent with infinitely many solutions.
Example 8: Show graphically that the system of equations
2x + 3y = 10, 4x + 6y = 12 has no solution.
Sol. The given equations are
2x + 3y = 10 ⇒ y = \(\frac { 10-2x }{ 3 }\)
| x | -4 | 2 |
| y | 6 | 2 |
| Points | A | B |
4x + 6y = 12 ⇒ y = \(\frac { 12-4x }{ 6 }\)
| x | -3 | 3 |
| y | 4 | 0 |
| Points | C | D |
Plot the points A (–4, 6), B(2, 2) and join them to form a line AB. Similarly, plot the points C(–3, 4), D(3, 0) and join them to get a line CD.
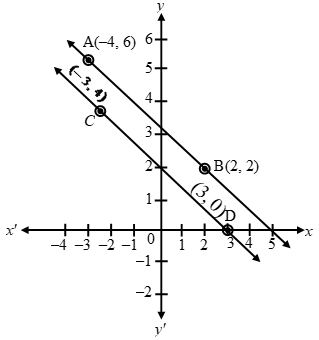
Clearly, the graphs of the given equations are parallel lines. As they have no common point, there is no common solution. Hence, the given system of equations has no solution.
Example 9: Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the
geometrical representing of the pair so formed is :
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Sol. We have, 2x + 3y – 8 = 0
(i) Another linear equation in two variables such that the geometrical representation of the pair so formed is intersecting lines is
3x – 2y – 8 = 0
(ii) Another parallel lines to above line is
4x + 6y – 22 = 0
(iii) Another coincident line to above line is
6x + 9y – 24 = 0
Example 10: Solve the following system of linear equations graphically;
3x + y – 11 = 0 ; x – y – 1 = 0
Shade the region bounded by these lines and also y-axis. Then, determine the areas of the region bounded by these lines and y-axis.
Sol. We have,
3x + y – 11 = 0 and x – y – 1 = 0
(a) Graph of the equation 3x + y – 11 = 0
We have, 3x + y – 11 = 0
⇒ y = – 3x + 11
When, x = 2, y = –3 × 2 + 11 = 5
When, x = 3, y = – 3 × 3 + 11 = 2
Plotting the points P (2, 5) and Q(3, 2) on the graph paper and drawing a line joining between them, we get the graph of the equation 3x + y – 11 = 0 as shown in fig.
(b) Graph of the equation x – y – 1 = 0
We have,
x – y – 1 = 0
y = x – 1
When, x = – 1, y = –2
When, x = 3, y = 2
Plotting the points R(–1, –2) and S(3, 2) on the same graph paper and drawing a line joining between them, we get the graph of the equation x – y – 1 = 0 as shown in fig.
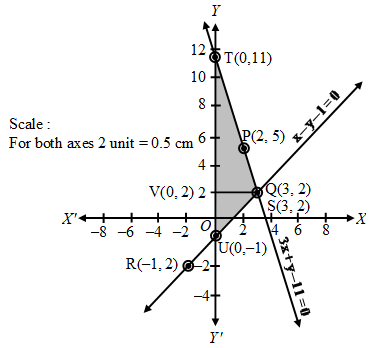
You can observe that two lines intersect at
Q(3, 2). So, x = 3 and y = 2. The area enclosed by the lines represented by the given equations and also the y-axis is shaded.
So, the enclosed area = Area of the shaded portion
= Area of ∆QUT = 1/2 × base × height
= 1/2 × (TU × VQ) = 1/2 × (TO + OU) × VQ
= 1/2 (11 + 1) 3 = 1/2 × 12 × 3 = 18 sq.units.
Hence, required area is 18 sq. units.
Example 11: Draw the graphs of the following equations
2x – 3y = – 6; 2x + 3y = 18; y = 2
Find the vertices of the triangles formed and also find the area of the triangle.
Sol. (a) Graph of the equation 2x – 3y = – 6;
We have, 2x – 3y = – 6 ⇒ y = \(\frac { 2x+6 }{ 3 }\)
When, x = 0, y = 2
When, x = 3, y = 4
Plotting the points P(0, 2) and Q(3, 4) on the graph paper and drawing a line joining between them we get the graph of the equation 2x – 3y = – 6 as shown in fig.
(b) Graph of the equation 2x + 3y = 18;
We have 2x + 3y = 18 ⇒ y = \(\frac { -2x+18 }{ 3 }\)
When, x = 0, y = 6
When, x = – 3, y = 8
Plotting the points R(0, 6) and S(–3, 8) on the same graph paper and drawing a line joining between them, we get the graph of the equation 2x + 3y = 18 as shown in fig.
(c) Graph of the equation y = 2
It is a clear fact that y = 2 is for every value of x. We may take the points T (3, 2), U(6, 2) or any other values.
Plotting the points T(3, 2) and U(6, 2) on the same graph paper and drawing a line joining between them, we get the graph of the equation y = 2 as shown in fig.
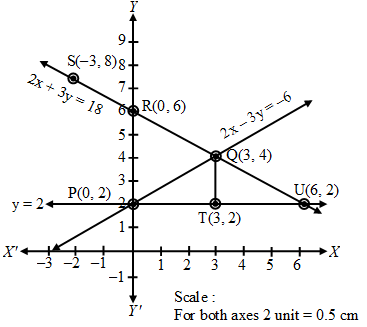
From the fig., we can observe that the lines taken in pairs intersect each other at points Q(3, 4), U (6, 2) and P(0, 2). These form the three vertices of the triangle PQU.
To find area of the triangle so formed
The triangle is so formed is PQU (see fig.)
In the ∆PQU
QT (altitude) = 2 units
and PU (base) = 6 units
so, area of ∆PQU = (base × height)
= 1/2 (PU × QT) = 1/2 × 6 × 2 sq. untis
= 6 sq. units.
Example 12: On comparing the ratios \(\frac{{{a}_{1}}}{{{a}_{2}}},\frac{{{b}_{1}}}{{{b}_{2}}}and\frac{{{c}_{1}}}{{{c}_{2}}}\) and without drawing them, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincide.
(i) 5x – 4y + 8 = 0, 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0, 18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0, 2x – y + 9 = 0
Sol. Comparing the given equations with standard forms of equations a1x + b1y + c1 = 0 and
a2x + b2y + c2 = 0 we have,
(i) a1 = 5, b1 = – 4, c1 = 8;
a2 = 7, b2 = 6, c2 = – 9
\( \frac{{{a}_{1}}}{{{a}_{2}}}=\frac{5}{7},\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-4}{6} \)
\(\Rightarrow \frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}} \)
Thus, the lines representing the pair of linear equations are intersecting.
(ii) a1 = 9, b1 = 3, c1 = 12;
a2 = 18, b2 = 6, c2 = 24
\( \frac{{{a}_{1}}}{{{a}_{2}}}=\frac{9}{18}=\frac{1}{2},\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{3}{6}=\frac{1}{2}and\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{12}{24}=\frac{1}{2}\)
\(\Rightarrow \frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}} \)
Thus, the lines representing the pair of linear equation coincide.
(iii) a1 = 6, b1 = – 3, c1 = 10;
a2 = 2, b2 = – 6, c2 = 9
\( \frac{{{a}_{1}}}{{{a}_{2}}}=\frac{6}{2}=3,\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-3}{-1}=3and\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{10}{9} \)
\(\Rightarrow \frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}} \)
Thus, the lines representing the pair of linear equations are parallel.