Factoring Trinomials
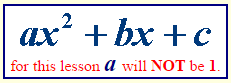
In the Algebra lesson on factoring trinomials where a = 1, we learned that factoring may require that we put our investigative skills to work. Those skills will really be put to the test when our trinomial starts with an a-value other than one. As with all factoring, there are several different methods that may be used. Let’s see what is involved in the “Set-up, Guess and Check” Method.
Let’s see what is involved with factoring
![]()
1. First, check to see if all of the terms share a common factor which may be removed. If each term can be factored before you begin, your work will be easier. The terms in this problem do not have a common factor.
2. Consider all of the possible factors of the leading coefficient, 2x². In this problem we only have one choice, 2x and x, making our work easy. So we can start with:(2x ) (x )
If the leading coefficient has several factors, make a list of the possible combinations, so as to be sure to include all possibilities.
3. Consider all of the possible factors of the last term, -6. The possible factors are:
+6 and -1
-6 and +1
+3 and -2
-3 and +2
You need to consider all of the possible ways of obtaining the number -6.
It appears that we have a multitude of “possible” answers:
(2x + 6)(x – 1)
(2x – 6)(x + 1)
(2x + 3)(x – 2)
(2x – 3)(x + 2)
(x + 6)(2x – 1)
(x – 6)(2x + 1)
(x + 3)(2x – 2)
(x – 3)(2x + 2)
4. We need to find the one “true” answer that will produce the desired middle term of -x. Test each of the possible answers to see which will yield the correct middle term.
(2x + 6)(x – 1) gives middle term 4x.
(2x – 6)(x + 1) gives middle term -4x.
(2x + 3)(x – 2) gives middle term -x. YEA!!!!!
(2x – 3)(x + 2) gives middle term +x.
(x + 6)(2x – 1) gives middle term 11x.
(x – 6)(2x + 1) gives middle term -11x.
(x + 3)(2x – 2) gives middle term 4x.
(x – 3)(2x + 2) gives middle term -4x.
5. Answer:
![]()
Notice: While we initially had several options for answers, we really had only one true answer. The more options that a problem creates, the more detective work needed to find the true answer.