Veerendra

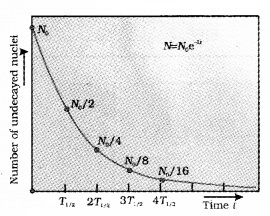
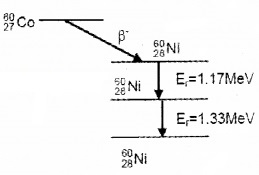
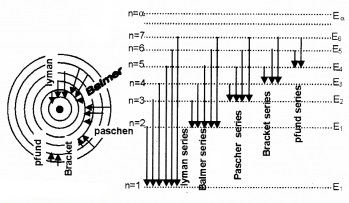
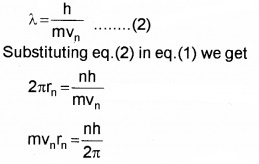
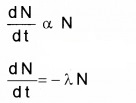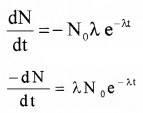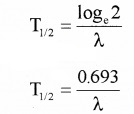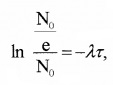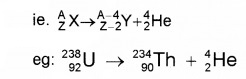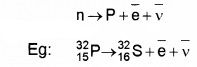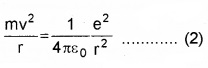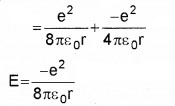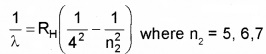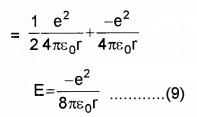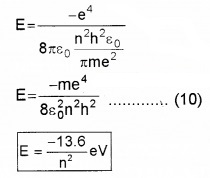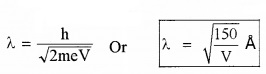Plus Two Physics Notes Chapter 14 Semiconductor Electronics: Materials, Devices and Simple Circuits is part of Plus Two Physics Notes. Here we have given Plus Two Physics Notes Chapter 14 Semiconductor Electronics: Materials, Devices and Simple Circuits.

Kerala Plus Two Physics Notes Chapter 14 Semiconductor Electronics: Materials, Devices and Simple Circuits

Introduction
Before the discovery of transistor, vacuum tube or valves were considered as the building blocks of electronic circuit.

1. A Comparison of Vacuum Tubes and Transistors:

Classification Of Metals, Conductors, And Semiconductors
1. On the basis of conductivity:
On the basis of relative values of electrical conductivity (σ) and resistivity ρ = \(\frac{1}{\sigma}\) solids are classified as

(i) Metals:
They possess very low resistivity (or high conductivity).
ρ → 10^-2 – 10^-8 Ω m
σ → 10² – 10⁸ S m^-1

(ii) Semiconductor:
They have resistivity or conductivity intermediate to metals and insulators.
ρ → 10^-5 – 10⁶ Ω m
σ → 10⁵ – 10^-6 S m^-1

(iii) Insulators: They have high resistivity (or low conductivity).
ρ → 10¹¹ – 10¹⁹ Ω m
σ → 10^-11 – 10^-19 S m^-1

2. Band Theory: Conduction Band, Valence Band, and Energy Gap:
In an isolated atom, electrons will have definite energy level. When atoms combine to form solid, the energy levels of outer electrons overlap. Hence outer energy levels split in to many energy levels.

These energy levels are very closely spaced Hence it appears as continuous variation of energy. This collection of energy levels are called energy band.

The energy band which includes energy levels of valence electrons is called valence band. The energy band above valence band which includes energy levels of conduction electrons is called conduction band.

The gap between the top of valence band and bottom of conduction band is called energy band gap (Energy gap, E_g).
Energy level diagram of different bands:

The band gap energy of Ge and Si are 0.3ev and 0.7ev respectively.

3. Classification on the basis of Energy bands Conductors:
Conduction band is partially filled and valence band is partially empty.

OR

Conduction band and valence band are overlapped so that E_g = 0ev

Due to overlapping, electrons are partially filled in conduction band. These partially filled electrons are responsible for current conduction.

Insulators:

Conduction band is empty. Valence band may fully or partially filled. There is a wide energy gap between valence band and conduction band (E_g > 3ev).

Semiconductors:
Conduction band may be empty or lightly filled. Valence band is fully filled. The energy gap is very small (< 3ev)

At room temperature some electrons in valence band get enough energy to cross the energy gap and move into conduction. Hence semiconductors show intermediate conductivity.

Intrinsic Semiconductor
A semiconductor in its pure form is called intrinsic semiconductor.

For intrinsic semiconductor:
* The number of free electrons is equal to number of holes.
ie. n_e = n_h = n_i
n_e, n_h and n_i are the free electron concentration, hole concentration and intrinsic carrier concentration.

Explanation:
Each Si atom is covalently bonded to nearest four neighboring atoms. When temperature increase, some of covalent bond brakes and electrons become free leaving a vacancy (hole). Thus each free electron creates hole in the lattice. Hence number of free electrons equals number of holes.

* The total current in intrinsic semi conductor is the sum of free electron current I_e and hole current I_h.
I = I_e + I_h

Explanation:
When an electric field is applied, free electrons move towards positive potential and give rise to electron current, le. The holes move towards negative potential and give rise to hole current. Thus total current is contributed by both free electrons and holes.

Extrinsic Semiconductor
1. Extrinsic semiconductor or impurity semiconductor:
The addition of suitable impurity improves the conductivity of intrinsic semiconductors. Such semiconductors are called extrinsic semiconductor. They are of two types n-type and p-type semiconductors.

2. Doping and Dopants:
The deliberate addition of suitable impurity to semiconductors to improve its conductivity is called doping.
The impurity atoms are called dopants. There are two types of dopants;

• Pentavalent (valency 5): Arsenic (As), Antimony (Sb), Bismuth (Bi), Phosphorous (P), etc.
• Trivalent (Valency 3): Indium (In), Boron (B), Aluminium (Al), etc.

3. n-type semiconductor:
When a pentavalent impurity is added to Si crystal, four electrons of impurity atom make bond with neighboring four Si atoms. The fifth electron remains weakly bound to its parent atom.

At room temperature this electron become free to move. Thus each pentavalent atom donate one extra electron for conduction and hence it is called donor impurity.

Thus in doped semiconductor the number of conduction electrons will be large compared to number of holes. Hence electrons are the majority carriers and holes the minority carriers. Hence semiconductors doped with pentavalent impurity is called n-type semiconductor.
Note:
In n-type semiconductors
n_e >> n_h
But as a whole n-type semiconductor is neutral (ie. electrons is equal and opposite to ionized (donor) core in lattice).

4. p-type semiconductor:
When a trivalent impurity is added to Si crystal, three electrons of impurity atom make covalent bond with neighboring three Si atom. The fourth bond with neighboring Si atom lacks one electron. Thus a vacancy or a hole is created in fourth bond.

The neighboring Si atom needs an electron to fill the vacancy and hence one electron in outer orbit of nearby Si atom move to this vacancy leaving a hole in its own site. Thus hole can move through the lattice.

Each trivalent atom creates a hole and it act as acceptor. Hence it is called acceptor impurity. The semiconductor doped with trivalent impurity has more number of holes than free electrons. Here holes are the majority carriers and electrons are the minority carriers. Hence it is called p-type semiconductor.
Note: I
(I) In p-type semi conductor
n_h >> n_e
But as a whole p-type semiconductor is electrically neutral. (The charge of additional holes is equal and opposite to acceptor ions).

(II) In thermal equilibrium electron and hole concentration in a semiconductor is given by n_en_h = n²_r.

5. Energy band structure of Extrinsic semiconductors
n-type semiconductor:

In n-type semiconductors, the donor energy level (E_D) is slightly below conduction band.

P-type semiconductor:

In p-type semiconductors, the acceptor energy level (E_A) lies slightly above valence bond.

p-n Junction
A p-n junction is basic building block of semiconductor devices like diode, transistor, etc.

1. p-n junction formation:
When pentavalent impurity is added to a part of p-type Si semiconductor wafer, we get both p region and n region in a single wafer.
The formation of p-n junction includes two processes.

(i) Diffusion:
In n type semiconductor, concentration of electrons is more than that of holes. In p-region, the hole concentration is more than electron concentration. Because of this concentration gradient, electrons diffuse from n side to p-side and holes diffuse from p-side to n-side during the formation of p-n junction. This produces diffusion current.

(ii) Drifting – Formation of Depletion region:

When electrons diffuses from n to p, it leaves behind positively charged immobile donor ions on n-side. As electrons continue to diffuse from n to p, a layer of positive charge is developed on n- side.

Similarly when holes diffuse from p to n, it leaves behind negatively charged immobile ions on p side. As holes continue to diffuse from p to n, negative space charge region is developed on p side.

The positive space-charge region on n-side and negative space-charge region on p-side, is known as depletion region. This region contain only immobile ions.

2. Barrier Potential:
The n-region losses electrons and p-region gains electrons. Because of this a potential is developed across the junction. This potential is called barrier potential.

Semiconductor Diodes
A semiconductor diode is a p-n junction provided with metallic contact at both ends to apply external voltage.
The symbol of p-n junction diode is given below.

The arrow shows conventional direction of current.

1. p-n junction diode under forward bias:
When p-side of p-n junction diode is connected to positive terminal of the battery and n-side to the negative terminal it is said to be in forward biased.

Due to the applied voltage, electrons of n-side get repelled by negative terminal of battery. Hence they cross depletion region and reach at p-side.

similarly the holes of p-side get repelled by positive terminal of battery and cross depletion region, reach n-side. The total forward current is sum of hole current and current due to electron.

2. p-n junction diode under reverse bias:
When p-side of p-n junction diode is connected to negative terminal of battery and n-side to the positive terminal, it is said to be in reversed biased.

In reverse bias the electrons of n-side and holes on p-side cannot cross the junction. But the minority carriers – holes on n-side and electrons on p-side drift across the junction and produce current. The reverse current is of the order micro ampere.
Note: Junction width increases in reverse bias.

Breakdown Voltage (V_Br):
The reverse current remains independent of bias voltage up to a critical reverse bias voltage called reverse break down voltage. At breakdown voltage, reverse current increases sharply.

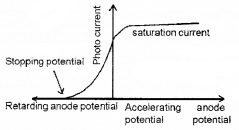
V-I characteristics:
To study variation of current with voltage for p-n junction diode, it is connected to a battery through a rheostat. Rheostat is used to vary the biasing voltage. A milliammeter is connected in series with diode to study forward current.

To measure reverse current microammeter is used. A voltmeter is connected across diode to measure voltage. The current is measured for different values of volt and a graph (V-I) is plotted.

In forward bias, current first increases very slowly up to a certain value of bias voltage. After this voltage, diode current increases rapidly. This voltage is called Knee voltage or cut-in voltage or threshold voltage. (0.2v for Ge and 0.7v for Si). The diode offers low resistance in forward bias.

In reverse bias, current is very small. It remains almost constant up to break down voltage (called reverse saturation current). Afterthis voltage reverse current increases sharply.
Note:
(i) In forward bias, resistance is low compared to reverse bias.
(ii) The dynamic resistance of diode is defined as ratio of change in voltage to change in current.
r_d = \(\frac{\Delta v}{\Delta l}\)

Application Of Junction Diode
Diode as a rectifier:
The process of converting AC into DC is known as Rectification. A p-n junction diode conducts current when it is forward biased, and does not conduct when it is reverse biased. This feature of the junction diode enables it to be used as rectifier.

1. Diode as half wave rectifier:

Circuit details:
A half wave rectifier consists of transformer, a diode and a load resistor R_L. The primary coil of transformer is connected to a.c input and secondary is connected to R_L through diode.

Working:
During the positive half cycle of the input a.c at secondary, the diode is forward biased and hence it conducts through R_L. During negative half cycle of a.c at secondary, diode is reverse biased and does not conduct. Thus, we get +ve half cycle at the output. Hence the a.c input is converted into d.c output.

2. Full wave rectifier:
Circuit details:

Full wave rectifier consists of transformer, two diodes, and a load resistance R_L. Input a.c signal is applied across the primary of the transformer. Secondary of the transformer is connected to D₁ and D₂. The output is taken across R_L.

Working:
During the +ve half cycle of the a.c signal at secondary, the diode D₁ is forward biased and D₂ is reverse biased. So that current flows through D₁ and R_L.

During the negative half cycle of the a.c signal at secondary, the diode D₁ is reverse biased and D₂ is forward biased. So that current flows through D₂ and R_L.

Thus during both the half-cycles, the current flows through R_L in the same direction. Thus we get a +ve voltage across R_L for +ve and -ve input. This process is called full-wave rectification.

Special Purpose p-n Junction Diodes
1. Zener diode:
Zener diode is designed to operate under reverse bias in the breakdown region. It is used as a voltage regulator. The symbol for Zener diode is shown in figure.

Zener diode is heavily dopped. Hence depletion region is very thin.
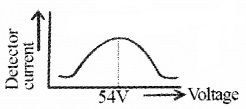
I-V characteristics of zener diode:

The l-V characteristics of a Zener diode is shown in above figure. At break down voltage, current increases rapidly. After breakdown, zener voltage remains constant. This property of the Zenerdiode is used for regulating supply voltages.

Explanation for large reverse current:
Reverse current is due to the flow of electrons (minority carriers) from p to n and holes from n to p. When the reverse bias voltage increases and becomes V = V₂ high electric field is developed. This high electric field can pull valence electrons from the atoms. These electrons account for high current.

1. (a) Zener diode as avoltage regulator Principle:
In reverse breakdown region, the voltage across the diode remains constant.
Circuit details:

The Zener diode is connected to a fluctuating voltage supply through a resistor R_z. The output is taken across R_L.

Working:
Whenever the supply voltage increases beyond the breakdown voltage, the current through zener increases (and also through R_z).

Thus the voltage across R_z increases, by keeping the voltage drop across zenerdiode as a constant value. (This voltage drop across R_z is proportional to the input voltage).

2. Optoelectronic junction devices:
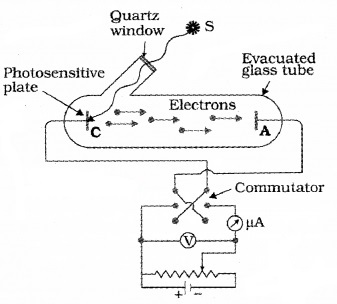
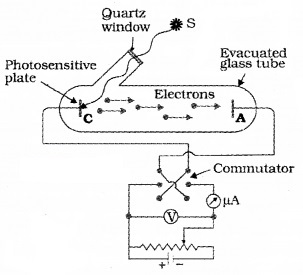
(i) Photodiode:
The photodiode can be used as a photodetector to detect optical signals.

It is operated under reverse bias. When the photodiode is illuminated with light (photons) electron-hole pairs are generated. Due to electric field of the junction, electrons and holes are separated before they recombine.

The direction of the electric field is such that electrons reach n-side and holes reach p-side. Electrons collected on n-side and holes collected on p- side produce an emf. When an external load is connected, the current flows through the load.
The I-V characteristics of a photodiode:

(ii) Light-emitting diode [LED]:
LED is heavily doped pn junction diode working under forward bias .Gallium Arsenide is used for making infrared LEDs.

Working:
When the junction diode is forward biased, electrons and holes flow in opposite directions across junction. Some of the electrons and holes combine at junction and energy is produced in the form of light.

Uses:
LEDs are used in remote controls, burglar alarm systems, optical communication, etc.

Advantages of LED over conventional incandescent lamps:

1. Low operational voltage and less power.
2. Fast action and no warm-up time required.
3. The bandwidth of emitted light is 100 A° to 500 A° or in other words it is nearly (but not exactly) monochromatic.
4. Long life and ruggedness.
5. Fast on-off switching capability.

3. Solar cell:
Solar cell is junction diode used to convert solar energy into electrical energy.
Circuit details:

Its p-region is thin and transparent and is called emitter. The n-region is thick and is called base. Output is taken across R_L.

Working:
When light falls on this layer, electrons from the n-region cross to the p-region and holes in the p-region cross in to the n-region. Thus a voltage is developed across R_L. Solar cells are used to charge storage batteries during daytime.
The I-V characteristics of a solar cell:

The I-V characteristics of solar cell is drawn in the fourth quadrant of the coordinate axes. This is because a solar cell does not draw current but supplies the same to the load.

Junction Transistor
1. Transistor: structure and action
Transistor is a three-layered doped semiconductor device. There are two types of transistors:

• n-p-n transistor
• p-n-p transistor.

Symbols:

Naming the transistor terminals:
A transistor has 3 terminals:

1. Emitter
2. Collector
3. Base.

1. Emitter:
The section, which supplies charge carriers, is called emitter. Emitter is heavily doped. The emitter should be forward biased.

2. Collector:
The section which collects the charge carriers, is called collector. Collector is moderately doped. The collector should be reverse biased.

3. Base:
Middle section between emitter and ‘ collector is called base. Base is lightly doped.

Transistor action:
Circuit details:
Emitter is maintained at forward bias and collector is maintained at reverse bias. V_EB is the emitter base voltage and V_CB is the collector base voltage.

Working:
Emitter is kept at forward bias so that the electrons are ejected into base. Thus an emitter current I_E is produced.

At the base, electron-hole combination takes place. As the base is lightly doped and very thin, only a few electrons combine with holes to constitute the base current, I_B.

The remaining electrons are attracted towards collector because the collector is kept at reverse bias. Due to this electron flow, a collector current I_C is produced.

In this way, the emitter current is divided into base current and collector current.
Mathematically this can be written as
I_E = I_B + I_C
I_B > is small, so I_E = I_C

2. Basic transistor circuit configurations and transistor characteristics:
Transistor can be used in three modes:

• Common base configuration
• Common emitter configuration
• Common collector configuration

a. Common base configuration:

In Common base configuration .base is common to both input and output
Current amplification = \(\frac{\text { output current }}{\text { input current }}\)
Current amplification, α = \(\frac{l_{C}}{l_{E}}\)

b. Common emitter configuration:

Current amplification = \(\frac{\text { output current }}{\text { input current }}\)
Current amplification, β = \(\frac{l_{C}}{l_{B}}\)

c. Common collector configuration:
Current amplification γ = \(\frac{l_{E}}{l_{B}}\)

Relation between α and β:
i.e. β = \(\frac{\alpha}{I-\alpha}\)
Common Emitter Configuration:

Input Characteristics (CE configuration):
The graph connecting base current with base-emitter voltage (at constant V_CE) is the input characteristics of the transistor.

To study the input characteristics, the collector to emitter voltage (V_CE) is kept at constant. The base current I_B against V_BE is plotted in a graph.
The ratio ∆ V_BE/∆ I_B at constant VCE is called the input resistance.
i.e,,Input resistance \(r_{1}=\frac{\Delta V_{B E}}{\Delta I_{B}}\)

Output Characteristics (CE. Configuration):
The output characteristics is a graph connecting the collector current lc with collector-emitter voltage (V_CE) at a constant base current (I_B).

This is obtained by measuring the collector current I_B at different collector voltage by keeping the base current fixed.

Line OA is called saturation line .The region right of the saturation line is the active region. Transistor is operated as amplifier in this region. The region below I_B = 0 is the cut off region.

The output resistance is the ratio of a small change in collector voltage to the change in collector current at constant base current.
Output resistance \(\mathrm{r}_{0}=\frac{\Delta \mathrm{V}_{\mathrm{CE}}}{\Delta \mathrm{I}_{\mathrm{C}}}\)

3. Transistor as a device
Transistor as a switch:
A circuit diagram for transistor switch is given below.

Applying Kirchoff’s voltage rule to the input side of this circuit, we get
V_BB = I_BR_B + V_BE
and applying Kirchoff’s voltage rule to the output side of this circuit, we get
V_CE = V_CC – I_CR_C.
We shall treat V_BB as the dc input voltage V_i and V_CE as the dc output voltage V_o.
So, we have
V_i = I_BR_B + V_BE ____(1) and
V_o = V_CC – I_CR_i______(2)

The variation of output voltage with input voltage:

The variation of output voltage with input voltage is shown in the above graph. This graph contain three regions

• cut off region
• Active region
• saturation region.

a. Cut off region:
In the case of Si transistor, if input voltage V_i is less than 0.6V, the transistor will be in cut off state and out put current (I_c) will be zero.
Substituting I_c = 0 in the eq (2) we get out put voltage V_o = V_CC

b. Active region:
When V_i becomes greater than 0.6 V the transistor is in active state with some current I_c. The eq(2) shows that, the output V_o decrease as the term I_cR_c increases. With increase of V_i, I_c increases almost linearly and so V_o decreases linearly till its value becomes less than about 1.0 V.
Note:
Amplifier is working in the active region.

c. saturation region:
When the output voltage becomes 1.0V, the change becomes non linear and transistor goes into saturation state. With further increase in V_i the output voltage is found to decrease towards zero (though it may never become zero).

Working of transistor as switch:
When V_i is low (unable to give forward-bias to the transistor) we get high output (ie. V_o = V_cc). In this stage the transistor doesn’t conduct. Hence transistor is said to be switched off.

If V_i is high enough to drive the transistor into saturation, then V_o is low (very near to zero). In this stage the transistor driven into saturation it is said to be switched on.
Note:
The switching circuits are designed in such a way that the transistor does not remain in active state.

4. Transistoras an Amplifier (CE-Configuration):

The working of an amplifier can be explained using the circuit given above. It is an n-p-n transistor connected in common emitter configuration. V_BB is the biasing voltage used in the input side and V_cc is the reverse bias voltage used in the output side.

R_B is the resistor connected to base in order to reduce the base current. R_c is the resistor which is connected in between V_cc and collector terminal. We take the voltage across R_c and V_cc with the help of a capacitor C. We maintain voltages V_BB and V_cc such that the transistor is always on the active region.

Working:
Case 1:
When there is no input signal (ie. V_i = 0,)
The input voltage can be written as
V_BB = V_BE + I_BR_B
This base voltage produces a base current I_B which in turn produces a dc collector current I_C. The output voltage can be written as
V_CE = V_CC – I_CR_C
This dc output voltage is unable to produce an output signal due to the presence of a capacitor. Because, the capacitor prevents the flow of dc current through it.

Case 2:
When there is an input ac signal, (ie. V_i ≠ 0):
when we apply an AC signal as input, we get an AC base current denoted by i_B. Hence input AC voltage can be written as
V_i = i_Br ______(1)
where ‘r’ is the effective input resistance.
This AC input current produces an AC output current (i_c) which can flow through a capacitor. Hence the output voltage can be written as
V₀ = i_c × output resistance
If we take output resistance as R_L then v_o becomes
V₀ = i_c R_L
V₀ = β_AC i_c × R_L _____(2) [since β_AC = \(\frac{\mathrm{i}_{\mathrm{C}}}{\mathrm{i}_{\mathrm{B}}}\)]

Power gain:
The power gain Apcan be expressed as the product of the current gain and voltage gain.
ie. power gain A_ρ = β_ac × A_v
Note:
The transistor is not a power generating device. The energy for the higher ac power at the output is supplied by the battery.

5. Feedback amplifier and transistor oscillator 9.13 Oscillator:
A transistor amplifier can be converted into an oscillator by positive feedback, (positive feedback means that a small portion of the output signal is applied to the input in-phase).

Circuit Details:
The battery V_cc is connected in between C (collector) and E (emitter) through a coil L¹. Another coil Lis connected in between B (base) and E. A capacitor is connected in parallel to coil L.

Working:

When the key is pressed a small current flows through the coil L¹1. The variation of current in the coil L¹ produces a change in flux. This change in flux induces a voltage across L.

As a result, the forward voltage increases which further increases the emitter and collector current. This again increases the forward voltage. This process continues till the collector gets saturated.

When the collector current is saturated (constant), the flux also becomes steady and the induced emf becomes zero. This reduces collector current. The decrease in collector current induces a voltage in L in the opposite direction (reverse voltage). As a result the collector current decreases further.

This continues until the collector current falls below its normal value. After this, the collector current build up and the process is repeated. Thus oscillation of frequency.
f = \(\frac{1}{2 \pi \sqrt{L C}}\) is produced.

Digital Electronics And Logic Gates
In digital electronics, we use two levels of voltage (represented by 0 and 1). Such signals are called digital signals. Logic gates are the building blocks of digital circuits. Logic gates are used in calculators, digital watches, computers, robots, industrial control systems, and in telecommunication.

1. Logic gates:
A logic gate is a digital circuit that follows certain logical relationship between input and output voltage. Hence it is so called. The funda¬mental logic gates are AND, OR, NOT, NAND, and NOR. The truth table gives all possible input logic level combinations with their respective output logic levels.

(i) NOT gate:
The most basic gate which has only a single input and single output. It is also called inverter. It produces an inverted version of input. The Boolean expression is y = \(\overline{\mathrm{A}}\)
The symbol is

A The truth table is

(ii) OR gate:
It has two or more inputs but a single output. The output is high when either inputs or both inputs are high.
The Boolean expression is Y = A + B (read as A or B)
The symbol is

The truth table:

(iii) AND gate:
It has two or more inputs but a single output. The output is high only if both inputs are high. The Boolean express of output is Y = A.B (read as A and B)
The symbol is

The truth table

(iv) NAND gate (or bubbled AND gate):
This is an AND gate followed by NOT gate. The Boolean expression is y = \(\overline{\mathrm{A.B}}\)
The symbol is

The truth table

(v) NOR gate (or bubbled OR gate):
It has two or more inputs and one output. This is OR gate followed by NOT gate.
The Boolean expression is Y = \(\overline{A+B}\)
The symbol is

The truth table is

NAND gate and NOR gate are called universal gates because other basic gates like OR, AND and NOT gate can be realized using them.

Integrated Circuits
The entire circuit fabricated on a small piece of semiconductor or chip is called Integrated Circuit (IC). It contains many transistors, diodes, resistors, capacitors, connecting wires – all in one package.

It was invented by Jack Kilky in 1958 and won Nobel prize for this invention. IC’s are produced by a process called photolithography. IC’s are categorized depending on nature of input signals.

(a) Linear or analogue IC:
These IC’s handle analogue signals and output varies linearly with input.
Eg: Operational Amplifier

(b) The digital IC:
These type handles digital signals and mainly contain logic gates Depending on the level of integration (number of circuit components or logic gates), IC are classified as

• SSI – Small scale Integration (logic gates ≤ 10)
• MSI – Medium Scale Integration (logic gates ≤ 100))
• LSI – Large scale Integration (logic gates ≤ 1000)
• VLSI – Very Large scale integration (logic gates > 1000)

The miniaturization in electronics technology is brought about by the Integrated circuit. It has made the things faster and smaller. IC is the heart of computer system. In fact IC’s are found in almost all electrical devices like cars, televisions, CD players, cell phones, etc.

We hope the Plus Two Physics Notes Chapter 14 Semiconductor Electronics: Materials, Devices and Simple Circuits help you. If you have any query regarding Plus Two Physics Notes Chapter 14 Semiconductor Electronics: Materials, Devices and Simple Circuits, drop a comment below and we will get back to you at the earliest.

Plus Two Physics Notes Chapter 13 Nuclei is part of Plus Two Physics Notes. Here we have given Plus Two Physics Notes Chapter 13 Nuclei.

Kerala Plus Two Physics Notes Chapter 13 Nuclei

Introduction
In this chapter, We shall discuss various properties of nuclei such as their size, mass and stability, and also associated nuclear phenomena such as radioactivity, fission and fusion.

Atomic Masses And Composition Of Nucleus
1. Atomic Mass Unit (amu or u):
The most commonly used unit to express atomic mass of nucleus is atomic mass unit (u). It is defined as 1/12^th of mass of carbon atom (C¹²).

2. Proton:
The nucleus of lightest atom (isotope) of hydrogen is called proton. The mass of proton is
m_p = 1.00727u = 1.67262 × 10^-27 kg
The charge of proton is +1.6 × 10^-19 and it is stable.

3. Discovery of Neutron:
Neutron was discovered by James Chadwick. He bombarded Beryllium nuclei with α particles and observed the emission of neutral radiation. He assumed the neutral radiation consists of neutral particles called neutron.

4. Neutron:
Neutron is changeless particle of mass 1.6749 × 10^-27kg. Neutron is stable inside nucleus but it is unstable in its free state.

5. Representation of Nuclide:
Nuclear species or nuclides are represented by notation ^A_ZX, where X is the chemical symbol of species.
Z → Atomic Number = Number of protons (electrons)
N → Neutron Number = Number of neutrons
A → Mass Number = Z + N (Total number of protons and neutrons)

6. Isotopes, Isobars and Isotones:

Size Of The Nucleus
The radius of nucleus is related to mass number (A) by the equation
R = R₀A^1/3
where ₀ = 1.2 × 10^-15 m
The volume of nucleus (the shape of nucleus is assumed to be spherical) is proportional to A.
ie. Volume = \(\frac{4}{3}\)πR³ = \(\frac{4}{3}\)R₀³.A
∴ Volume α A
The density of nucleus is constant. It is independent of A and its value is 2.3 × 10¹⁷kgm^-3

Mass Energy And Nuclear Binding Energy
1. Mass Energy:
According to Einstein mass is considered as a source of energy. The mass ‘m’ can be converted into energy according to relation
E = mc²
This is mass energy equivalence relation. C is the velocity of light (3 × 10⁸m/s).

2. Nuclear binding energy:
(A) Mass Defect:
The mass defect (Am) is the difference in the mass of nucleus and total mass of constituent nucleons.
∆m = (ZM_P + (A – Z)m_n] – M
m_P and m_n are mass of proton and neutron respectively. M is the mass of nucleus.
Eg: In ¹⁶₈O, there are 8 protons and 8 neutrons. The atomic mass of ¹¹₈O is 15.99493u. The expected mass of ¹⁶₈O is sum of masses of its nucleons.
Total mass of nucleons
= 8 × m_P + 8 × m_n
= 8 × 1.00727u + 8 × 1.00866u
= 16.12744u
The difference in mass,
∆m = 16.12744u – 15.99493u = 0.13691u

(B) Binding Energy and Binding Energy per nucleon (E_b and E_bn):
Binding Energy: Mass defect (∆m) gets converted into energy as
E_b = ∆mc²
This energy is called binding energy. Which binds nucleons inside the nucleus.

Binding Energy per nucleon:
Binding energy per nucleon E_bn is the ratio of binding energy of nucleus to number of nucleons
E_bn = \(\frac{E_{b}}{A}\)
E_bn is the measure of stability of nucleus.

(C) Plot of E_bn versus mass number, A Main features of the graph:

• E_bn is almost constant for nuclei whose mass number ranges as 30 < A < 170. The maximum value of E_bn is 8.75Mev for ⁵⁶Fe and it is 7.6MeV for ²³⁸U.
• E_bn is low for lighter nuclei and also for heavier nuclei.
• There appear narrow spikes in the curve.

The conclusions from the features of graph:

• The force is attractive and sufficiently strong.
• The nuclear force is short range. Each nucleon has its influence on its immediate neighbors only so nuclear force is saturated.
• Heavier nuclei like U²³⁸ have low E_bn. So it split up into nuclei of high Ebn releasing energy ie. it undergoes fission.
• Lighter nuclei like ²H, ³H, etc. have low E_bn. So it combine to form a heavier nuclei of high E_bn releasing energy ie. it undergoes nuclear fusion.
• The nuclei at the peaks of narrow spikes have high E_bn which shows extra stability.

Nuclear Force
The features of nuclear force are:

1. The nuclear force is the strongest force in nature.
2.  The nuclear force is saturated. It is short range force.
3. The nuclear force is charge independent ie. nuclear force between proton-proton, neutron-neutron, and proton-neutron are the same.

Variation of potential energy with distance:
The potential energy of a pair of nucleons as a function of their separation is shown in the figure

At a particular distance r₀, potential energy is minimum. The force is attractive when r > r₀ and it is repulsive when r < r₀. The value of r0 is about 0.8 fm.

Radioactivity
A.H. Becquerel discovered radioactivity.
In radioactive decay, unstable nucleus undergoes decay into stable one. There are three types of decay

1. α decay
2. β decay
3. γ decay

1. Law of Radioactive Decay:
According to Law of Radioactive decay, the number of nuclei undergoing decay per unit time (or rate of decay) is proportional to number of nuclei in the sample at that time.

λ is decay constant or disintegration constant. The negative sign indicates that number of nuclei is decreasing with time. The solution to the above differential equation is
N = N₀e^-λt
N₀ is the initial number of atoms. This equation shows that number of nuclei is decreasing exponentially with time as shown below.

Derivation of equation N(t) = N(0)e^-λt
According to Law of Radioactive decay,
\(\frac{d N}{d t}\) = -λn
\(\frac{d N}{d t}\) = -λdt
Integrating
InN = -λt + C_____(1)
C is the constant of integration. To get value of C, let us assume that initially (t = 0) the number of nuclei be N₀
∴ C = In N₀
Substituting for C in equation (1) we get,
InN – In N₀ = -λt
In\(\frac{N}{N_{0}}\) = -λt
\(\frac{N}{N_{0}}\) = e^-λt
N = N₀e-λt

(A) The decay rate (R):
The decay rate is number of nuclei disintegrating per unit time and is denoted by R.
R = \(\frac{-d N}{d t}\)
Differentiating the equation N = N₀e^-λt, we get

In terms of decay rate we get R = R₀e^-λt
where R₀ = λN₀, decay rate at t = 0

(B) Half life (T_1/2):
It is the time taken by radio nuclide to reduce half of its initial value.
half life period T_1/2 = \(\frac{0.693}{\lambda}\)
Relation between (T_1/2) and λ
If T_1/2 is the half-life period, then N = \(\frac{\mathrm{N}_{0}}{2}\)
Substituting these values in N = N₀e^-λt, we get,
\(\frac{\mathrm{N}_{0}}{2}\) = N₀e^-λT_1/2
2 = e^-λT_1/2
Taking log on both sides we get,
log_e2 = λT_1/2 (since log e^x = x)

(C) Mean life(t) or average life:
It is defined as time taken by radio nuclei to reduce 1/e^th of its initial value.
Mean life τ = \(\frac{1}{\lambda}\)
proof
We know In (\(\frac{N}{N_{0}}\)) = -λt

∴ t = τ, N = \(=\frac{N_{0}}{e}\)
In(1/e) = -λτ
In(e) = λτ
In e = 1
1 = λτ
∴ τ = 1/λ

(D) Relation between τ and T_1/2
T_1/2 = 693τ

(E) Units of Radioactivity:
The SI unit for radioactivity is Becquerel. One becquerel is one disinte¬gration per second. The traditional unit of activity is curie.
1 curie = 3.7 × 10¹⁰ Bq

2. Alpha Decay (α decay):
In α decay, mass number is reduced by 4 units and atomic number is reduced by 2 units.

Q-value
Q value is the energy released in nuclear reaction. The Q value or disintegration energy of a decay can be defined as the difference between the initial mass energy and final mass energy of decay products The Q value of a decay is expressed as
Q = (m_x – m_y – m_He)c²

3. Beta decay (β – decay): There are two types of β decay

• β⁺ decay
• β^– decay

a. β⁺ decay:
In β⁺ decay atomic number is reduced by 1 unit. But mass number remains unchanged.

In β⁺ decay, positron and neutrino are emitted. In β⁺ decay, conversion of proton into neutron, positron and neutrino takes place.

b. β^– decay:
In β^– decay, atomic number is increased by 1 unit. But mass number does not change.

In β^– decay a neutron converts into proton emitting electron and antineutrino.

4. Gamma Decay:
The excited nucleus comes back to ground state by emitting gamma rays.
Eg:

5. Properties of α, β and γ:
Properties of α – particle:

• α -particles have a charge of +2e and a mass four times that of hydrogen atom.
• They are deflected by electric and magnetic fields.
• They affect photographic plates.
• They produce fluorescence and phosphorescence.
• They have a high ionizing power.
• They can penetrate very thin metal foils.
• The velocity is of the order of 10⁷ m/s.

Properties of β – particles:

• β – particle is an electron.
• They are deflected by electric and magnetic fields.
• They can affect photographic plates.
• They can produce fluorescence and phosphorescence
• They have low ionization power.

Properties of γ – ray:

• γ – rays are electromagnetic waves.
• They have the speed of light.
• They have high penetrating power.
• They can affect photographic plates.
• They can produce fluorescence and phosphorescence.
• They have ionizing power.
• They are not deflected by electric and magnetic fields.

Nuclear Energy:
In nuclear reactions, huge quantity of energy is released

1. Fission:
In nuclear fission, heavier nuclei split into lighter ones releasing huge energy. When the Uranium atom is bombarded with neutron, it breaks into intermediate mass fragments as shown.

Note:

• The energy released perfission of Uranium nucleus is 200MeV.
• The neutrons released per fission of Uranium nucleus is 2.5
• Controlled chain reaction (nuclear fission) is basic principle of nuclear reactor.
• Uncontrolled chain reaction results in explosion. This is the principle behind atom bomb.

A. Chain reaction:
The nuclear fission (of U²³⁸) produces extra neutrons. These extra neutrons may bombard with the neighboring Uranium atoms and make it to undergo nuclear fission.

This fission again produces more neutrons. This process continues like a chain. This was first suggested by Enrico Fermi.

2. Nuclear Reactor:
The controlled chain reaction produce a steady energy output. This is the basic of nuclear reactor.
The main components of nuclear reactor:

(i) Fissionable material or fuel:
The fissionable material is (²³⁵₉₂U). Which is placed inside the core where the fission takes place.

(ii) Moderator:
It is used to slow down fast moving neutron. Commonly used moderators are water, heavy water (D₂O), and graphite.

(iii) Reflector:
The core is surrounded by reflector to prevent the leakage.

(iv) Control rods:
Its purpose is to absorb neutron and hence to control reaction rate. It is made up of neutron-absorbing material like Cadmium.

(v) Coolant:
The energy released in the form of heat is continuously removed by coolant. It transfers heat to the working fluid.

The whole assembly is properly shielded to prevent radiation from coming out. The working fluid gets converted into steam by heat and it drive turbines and generate electricity.

A. Multiplication Factor (K)
Multiplication factor is a measure of growth rate of neutrons. For steady power operation, value of K should be 1. (called critical stage). If K > 1, reaction rate increases exponentially.

3. Nuclear Fusion – Energy Generation in stars:
In nuclear fusion lighter nuclei combine to form heavier nuclei releasing energy. Nuclear fusion is thermo nuclear reaction. It occurs at high temperature. At high temperature, particles get enough kinetic energy to overcome Coulomb repulsion.

Thermonuclear fusion is the source of energy in sun. The fusion inside sun involves burning of hydrogen into Helium.

4. Controlled Thermonuclearfusion:
In future, we expect to build up fusion reactors to generate power. For this to happen, the nuclear fuel must be kept at a temperature 10⁸K.

At this temperature fuel exists in plasma state. The problem is that no container can stand such a high temperature. Several countries around world including India are developing techniques to solve this problem.

We hope the Plus Two Physics Notes Chapter 13 Nuclei help you. If you have any query regarding Plus Two Physics Notes Chapter 13 Nuclei, drop a comment below and we will get back to you at the earliest.

Plus Two Physics Notes Chapter 12 Atoms is part of Plus Two Physics Notes. Here we have given Plus Two Physics Notes Chapter 12 Atoms.

Kerala Plus Two Physics Notes Chapter 12 Atoms

Introduction
What is the arrangement of +ve charge and the electrons inside the atom? In other words, what is the structure of an atom?

Alpha-particle Scattering And Rutherford’s Nuclear Model Of Atom
Rutherford’s scattering experiment:

Experimental arrangement:
α particles are incident on a gold foil (very small thickness) through a lead collimator. They are scattered at different angles. The scattered particles are counted by a particle detector.

Observations:
Most of the alpha particles are scattered by small angles. A few alpha particles are scattered at an angle greater than 90°.

Conclusions

1. Major portion of the atom is empty space.
2. All the positive charges of the atom are concentrated in a small portion of the atom.
3. The whole mass of the atom is concentrated in a small portion of the atom.

Rutherford’s model of atom

1. The massive part of the atom (nucleus) is concentrated at the centre of the atom.
2. The nucleus contains all the positive charges of the atom.
3. The size of the nucleus is the order of 10^-15m.
4. Electrons move around the nucleus in circular orbits.
5. The electrostatic force of attraction (between proton and electron) provides centripetal force.

1. Alpha-particle trajectory and Impact parameter:
The impact parameter is the perpendicular distance of the initial velocity vector of the a particle from the centre of the nucleus.

It is seen that an α particle close to the nucleus (small impact parameter) suffers large scattering. In case of head-on collision, the impact parameter is minimum and the α particle rebounds back. For a large impact parameter, the α particle goes nearly undeviated and has a small deflection.

2. Electron orbits (Rutherford model of atom):
In Rutherford atom model, electrons are revolving around the positively charged nucleus. The electro-static force of attraction between the positive charge and negative charge provide centripetal force required for rotation.
For a dynamically stable orbit,
Centripetal force = Electrostatic force of attraction
F_c = F_e

Thus the relation between the orbit radius and the electrons velocity,

Total energy of electron of Hydrogen atom (Rutherford model atom):
From eq. (1), we get

∴ Kinetic energy of electron
KE = \(\frac{1}{2}\)mv² ……….(3)
Substituting eq.(2) in eq. (3) we get
KE = \(\frac{e^{2}}{8 \pi \varepsilon_{0} r}\) …………(4)
The electrostatic potential energy of hydrogen atom
\(\frac{e^{2}}{8 \pi \varepsilon_{0} r}\)
u = \(\frac{-e^{2}}{4 \pi \varepsilon_{0} r}\) ………..(5)
∴ The total energy E of the electron in a hydrogen atom
E = K.E + Potential energy (U)

The total energy of the electron is negative. This implies that the electron is bound to the nucleus.
If E is positive, the electron will escape from the nucleus.

Atomic Spectra
There are two types of spectra

1. Emission spectra
2. Absorption spectra

1. Emission spectra:
When an atomic gas or vapor is excited, the emitted radiation has a spectrum which contains certain wavelength only. A spectrum of this kind is termed as emission line spectrum. It consists of bright lines on a dark background.

Absorption spectra:
When white light passed through a gas, the transmitted light has spectrum contain certain wavelength only. A spectrum of this kind is termed as absorption line spectrum. It consists of dark lines on a bright background.

1. Spectral series:

The frequencies of the light emitted by a particular element exhibit some regular pattern. Hydrogen is the simplest atom and therefore, has the simplest spectrum, the spacing between lines of the hydrogen spectrum decreases in a regular way. Each of these sets is called a spectral series.

The first such series was observed by a Johann Jakob Balmer in the visible region of the hydrogen spectrum. This series is called Balmer series. Balmer found a simple empirical formula for the observed wavelengths.

where λ is the wavelength, R is a constant called the Rydberg constant, and n may have integral values 3, 4, 5, etc. The value of R is 1.097 × 10⁷m^-1. This equation is also called Balmer formula.

Other series of spectra for hydrogen were discovered. These are known, as Lyman, Paschen, Brackett, and Pfund series. These are represented by the formulae:
Lyman series:

Balmer series:

Paschen series:
This series is in the infrared region. For this series the electron must jump from higher orbit to the third orbit.

Bracket series:
This series is the infrared region, for this the electron must jump from higher energy level to fourth orbit.

P-fund series:
This series is in the infrared region.

Bohr Model Of Hydrogen Atom
Limitations of Rutherford model:
1. Circular motion is an accelerated motion, an accelerated charge emit radiations. So that electron should emit radiation. Due to this emission of radiation, the energy of the electron decreases. Thus the atom becomes unstable.

2. There is no restriction for the radius of the orbit. So that electron can emit radiations of any frequency.

Bohr postulates:
Bohr combined classical and early quantum concepts and gave his theory in the form of three postulates.

• Electrons revolve round the positively charged nucleus in circular orbits.
• The electron which remains in a privileged path cannot radiate its energy.
• The orbital angular momentum of the electron is an integral multiple of h/π.
• Emission or Absorption of energy takes place when an electron jumps from one orbit to another.

Radius of the hydrogen atom:
Consider an electron of charge ‘e’ and mass m revolving round the positively charged nucleus in circular orbit of radius ‘r’. The force of attraction between the nucleus and the electron is

This force provides the centripetal force for the orbiting electron

According to Bohr’s second postulate, we can write
Angular momentum, mvr \(=\frac{n h}{2 \pi}\).
ie. v = \(\frac{n h}{2 \pi m r}\) _____(4)
Substituting this value of ‘v’ in equation (2), we get

Energy of the hydrogen atom:
The K.E. of revolving electron is
K.E\(=\frac{1}{2}\) mv² ______(6)
Substituting the value of equation (3) in eq.(6), we get
K.E = \(\frac{1}{2} \frac{e^{2}}{4 \pi \varepsilon_{0} r}\) ______(7)
The potential energy of the electron,
P.E = \(\frac{-e^{2}}{4 \pi \varepsilon_{0} r}\) _______(8)
ie. The Total energy of the hydrogen atom is,
T.E = Ke + PE

Substituting the value of equation (5) in equation (9) we get

1. Energy levels
Ground state (E₁):
Ground state is the lowest energy state, in which the electron revolving in the orbit of smallest radius.
For ground state n = 1
∴ Energy of hydrogen atom E₁ = \(\frac{-13.6}{n^{2}}\) = -13.6 ev.

Excited State (E₂):
When hydrogen atom receives energy, the electrons may raise to higher energy levels. Then atom is said to be in excited state.

First Excited state:
For first excited state n = 2
∴ Energy of first excited state E₂ = \(\frac{-13.6}{2^{2}}\) = -3.04ev
Similarly energy of second excited state
E₃ = \(\frac{-13.6}{3^{2}}\) = -1.51ev

Energy difference between E₁ and E₂ of H atom:
The energy required to exist an electron in hydrogen atom to its first existed state.
∆E = E₂ – E₁ = ^–3.4 – ^–13.6 = 10.2eV.

Ionization energy:
Ionization energy is the minimum energy required to free the electron from the ground state of atom. (ie. n = 1 to n = ∞)
The ionization of energy of hydrogen atom = 13.6 ev

2. Energy level diagram of hydrogen atom:

Note:
An electron can have any total energy above E = 0ev. In such situations electron is free. Thus there is a continuum of energy states above E = 0ev.

The Line Spectra Of The Hydrogen Atom
According to the third postulate of Bohr’s model, when an atom makes a transition from higher energy state (n_i) to lower energy state (n_f), photon of energy hv_if is emitted.
ie. hν_if = E_ni – E_nf

De Broglie’s Explanation Of Bohr’s Second Postulate Of Quantization
Louis de Broglie argued that the electron in its circular orbit, behalf as a particle wave. Particle waves can produce standing waves under resonant conditions.
The condition to get standing wave,
2πr_n = nλ
n = 1, 2, 3……..
The quantized electron orbits and energy states are due to the wave nature of the electron.

DeBroglie’s Proof for Bohr’s second postulate:
According to De Broglie, the electron in a circuit orbit is a particle wave. The particle wave can produce standing waves under resonant conditions. The condition for resonance for an electron moving in n^th circular orbit of radius r_n,
2πr_n = nλ______(1)
n = 1, 2, 3………
If the speed of electron is much less than the speed of light, wave length

Note:
The quantized electron orbits and energy states are due to the wave nature of the electron.

Limitations of Bohr atom model:

1. The Bohr model is applicable to hydrogenic atoms. It cannot be extended to many electron atoms such as helium
2. The model is unable to explain the relative intensities of the frequencies in the spectrum.
3. Bohr model could not explain fine structure of spectral lines.
4. Bohr theory could not give a satisfactory explanation for circular orbit.

We hope the Plus Two Physics Notes Chapter 12 Atoms help you. If you have any query regarding Plus Two Physics Notes Chapter 12 Atoms, drop a comment below and we will get back to you at the earliest.

Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter is part of Plus Two Physics Notes. Here we have given Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter.

Kerala Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter

Introduction
The discovery of cathode rays by Rontgen and discovery of electrons by JJ Thomson were important milestones in the study of atomic structure.

Electron Emission
We know that metals have free electrons. The free electrons cannot normally escape out of the metal surface. If an electron attempts to come out of the metal, the metal surface acquires a positive charge. This positive surface held electrons inside the metal surface.

Work function:
When we give energy to electron in a metal, it can come out of metal. This minimum energy required by an electron to escape from the metal surface is called the work function of the metal. It is generally denoted by Φ₀(hν₀) and measured in eV (electron volt).

Electron volt:
One electron volt is the energy gained by an electron when it has been accelerated by a potential difference of 1 volt
1 eV = 1.602 × 10^-19J.
This unit of energy is commonly used in atomic and nuclear physics.

Different types of electron emission:
The minimum energy required for the electron emission from the metal surface can be supplied by any one of the following methods.

(i) Thermionic emission:
Electrons can come out of metal surface, if heat energy is given to metal.

(ii) Field emission:
By applying a very strong electric field (of the order of 10⁸ Vm^-1) to a metal, electrons can be pulled out of the metal.

(iii) Photoelectric emission:
When light (of suitable frequency) incident on a metal surface, electrons are emitted from the metal surface. These electrons are called photoelectrons. This phenomena is called photo electric effect.

Photoelectric Effect
1. Hertz’s observations:
The phenomenon of photoelectric emission was discovered by Heinrich Hertz in 1887, Heinrich Hertz observed that when light falls on a metal surface, electrons escape from the metal surface.

2. Hallwachs’ and Lenard’s observations:
Wilhelm Hallwachs and Philipp Lenard investigated the phenomenon of photoelectric emission in detail. The experimental set up consist of two metal plates (cathode and anode) inside a evacuated glass tube as shown in figure.

They observed that current flpws in the circuit when emitter plate (C) was illuminated by UV radiation. It means that when light incident on a metal plate electrons are emitted. These electrons move towards the anode and results in current flow.

They also observed that, when a negatively charged zinc plate is illuminated by UV light, it becomes chargeless. He also observed that uncharged Zn plate becomes positively charged when it is illuminated with UV light.

From these observations they concluded that the particles emitted carry negative charge.

Threshold frequency:
The minimum frequency (ν₀) required to produce photoelectric effect is called the threshold frequency. It depends on the nature of material.

Experimental Study Of Photoelectric Effect
The experimental setup:

The experimental arrangement consists of two zinc plates enclosed in a quartz bulb. The plates are connected to a battery through a micro ammeter. When ultraviolet light is incident on the cathode plate, the micrometer indicates a current in the circuit.

When the anode is made negative (with respect to cathode) the current decreases and at a certain voltage (V₀), current is completely stopped. This voltage V₀ is called stopping potential. At this stage,
\(\frac{1}{2}\) mV_max² = eV₀
where v_max is the maximum kinetic energy of photo electrons.

1. Effect of intensity of light on photocurrent Experiment:
In this experiment the collector A is maintained at a positive potential. The frequency of the incident radiation and the accelerating potential are kept at fixed.

Then change the intensity of light and measure photoelectric current in each time. Draw a graph between photo current and intensity of light. We get a graph as shown in figure.

Observations:
This graph shows that photocurrent increases linearly with intensity of incident light.

Conclusion:
The photocurrent is directly proportional to the number of photoelectrons emitted per second. This implies that the number off Photoelectrons emitted per second is directly proportional to the intensity of incident radiation.

2. Effect of potential on photoelectric current Experiment:
Keep the plate A at positive accelerating potential. Then illuminate the plate C with light (of fixed frequency v and fixed intensity I₁). Then vary the positive potential of plate A gradually and measure the resulting photocurrent each time.

When the photo current reaches maximum, the polarity of plates are reversed and thus apply a negative potential (retarding potential) to plate A.

Again photocurrent is measured by varying the retarding potential till photocurrent reaches zero. The experiment is repeated for higher intensity I₂ and I₃ keeping the frequency fixed.

Observations:
As accelerating potential increases photo current increases. At a particular anode potential photocurrent reaches maximum. Further increase in accelerating potential does not increase photo current.

When we apply negative potential to A, photo electrons get retarded and hence photocurrent decreases. At particular retarding potential photocurrent becomes zero. This potential is called cut off or stopping potential.

The graph of anode potential with photo current:

The saturation current is found to be large at higher intensity (because photo current is directly proportional to intensity). But stopping potential is same for different intensity at fixed frequency, (ie. for a given frequency of incident radiation stopping potential is independent of its intensity).

Note:
a. The maximum value of photo current is called saturation current (Isat).

b. The retarding anode potential at which photo current reaches zero is called stopping potential (V₀).

When retarding potential is applied, only most energetic electrons can reach collector plate A. At stopping potential no electrons reach plate A, ie stopping potential is sufficient to repel the electron with maximum kinetic energy

c. The stopping potential or maximum value of KE depends only on frequency of incident light, not on its intensity. Hence stopping potential is same for different intensity at constant frequency.

d. At zero anode potential, photocurrent is not zero, ie photo electric effect takes place even if anode potential is not applied.

3. Effect of frequency of incident radiation on stopping potential:
Experiment:
In this experiment, we adjust the intensity of light at various frequencies (say ν₁, ν₂ and ν₃ such that ν₁ < ν₂ < ν₃) and study the variation of photocurrent with collector plate potential.

Observations:

For frequencies ν₁, ν₂ and ν₃ (ν₁ < ν₂ < ν₃) τηε stopping potential are found to be V₀₃ > V₀₂ > V₀₁. It means that stopping potential varies linearly with incident frequency fora given photosensitive material.

The graph of stopping potential with frequency:

The graph shows that

• The stopping potential V₀ varies linearly with the frequency of incident radiation for a given photosensitive material,
• There exists a certain minimum cutoff frequency ν₀ for which the stopping potential is zero.

These observations have two implications:

• The maximum kinetic energy of the photoelectrons varies linearly with the frequency of incident radiation, but is independent of its intensity.
• Fora frequency ν of incident radiation, lower than the cutoff frequency ν₀, no photoelectric emission is possible even if the intensity is large.
• For a frequency ν₀, no photoelectric emission is possible even if the intensity is large. This minimum, cutoff frequency ν₀, is called the threshold frequency. It is different for different metals.

Summary of the experimental features and observations:
Laws of photoelectric emission:

1. For a given frequency of radiation, number of photoelectrons emitted is proportional to the intensity of incident radiation.
2. The kinetic energy of photoelectrons depends on the frequency of incident light but it is independent of the light intensity.
3. Photoelectric effect does not occur if the frequency is below a certain value. The minimum frequency (ν₀) required to produce photo electric effect is called the threshold frequency.
4. Photoelectric effect is an instantaneous phenomenon.

Photoelectric Effect And Wave Theory Of Light
Wage theory of light is not used to explain photoelectric effect. Why?
Reasons
1. According to wave theory, when intensity of incident wave increases, the KE of electron must be increased. This is pgainst the experimental observation of photoelectric effect.

2. According to wave theory, absorption of energy by electron takes place continuously. A large number of electrons absorb energy from the wave at a time.

Hence energy received by a single electron will be small. Hence it takes hours to eject an electron from a metal surface. This delay in photoemission is against the experimental observation.

Einstein’s Photoelectric Equation
Energy quantum of radiation:
Einstein explained photoelectric effect based on quantum theory. According to quantum theory, light contain photons having energy hν, when a photon of energy hr incidents on a metal surface, electrons are liberated.

A small portion of the photon energy is used for work function (Φ) and remaining energy is appeared as K.E of the electron.

By law of conservation of energy, we can write,
Photon energy = work function + K.E of electrons
hν = Φ + \(\frac{1}{2}\) mv²
\(\frac{1}{2}\)mv² = hν – Φ______(1)
If threshold frequency ν₀ is incident, we can take K.E = 0
So eq(1) can be written as
0 = hν₀ – Φ
i.e. work function Φ = hν₀______(2)
Substituting eq(2) in eq(1) we get
\(\frac{1}{2}\)mv² = hν – hν₀
\(\frac{1}{2}\)mv² = h(ν – ν₀)______(3)
This is Einstein’s Photoelectric equation.
But we know ν = c/λ and ν₀ = c/λ₀
Substituting these values in eq(3) we get,

Discussion (explanation of photo electric effect on the basis of Einstein’s photo electric equation):
1. If the intensity of the incident light increases, more number of photons interact with electrons and more number of electrons are emitted. Thus the electric current increases with the intensity of the incident light.

2. For a given metal, Φ₀(hν₀) is constant. Hence from 1/2mv² = hν – hν₀, we can understand that KE depends on ‘V’ (incident frequency).

3. From this equation 1/2mv² = hν – hν₀. we can understand that photoemission is not possible, if ν < ν_0.

4. According to quantum theory, a photon interacts only with a single electron (no sharing of energy takes place) so that there is no time delay in photoelectric emission.

Particle Nature Of Light: The Photon:
The photon picture of electromagnetic radiation is as follows:

1. In interaction of radiation with matter, radiation behaves as if it is made up of particles called photons.
2. Each photon has energy E and momentum ρ.
3. Photon energy is independent of intensity of radiation.
4. Photons are electrically neutral and are not deflected by electric and magnetic fields.
5. In a photon-particle collision the total energy and total momentum are conserved.

Wave Nature Of Matter
In 1924, the French physicist Louis Victorde Broglie put forward the hypothesis, that moving particles of matter should display wavelike properties under suitable conditions.

The waves associated with material particles are known as matter waves or de-Broglie’s waves. de-Broglie wave is seen with microscopic particles like proton, electron, and neutron, etc. The wave length of matter waves is called de-Broglie wave length.
De-Broglie wave length,

h – Plank’s constant, m – mass of the particle, v – velocity of the particle.

1. Wavelength of matter waves:
The energy of photon E = hν _____(1)
If photon is considered as a particle of mass ‘m’, the energy of photon can be written as
E = mc² _____(2)
From eq(1) and eq (2) we get
hν = mc²
m = \(\frac{\mathrm{hv}}{\mathrm{c}^{2}}\) ________(3)
Momentum of the electron can be written as
P = mass × velocity ______(4)
Substituting eq (3) in eq(4) ,we get

The wave length of electron wave:
If electron of mass ‘m’ and charge ‘e’ is accelerated through a p.d of V volt, the de-Broglie wavelength can be written as

2. Uncertainty Principle:
According to the principle, it is not possible to measure both the position and momentum of an electron (or any other particle) at the same time exactly.

If (∆x) is the uncertainty in position and (∆p) is the uncertainties in momemtum, the product uncertainties is given by
∆x.∆p =\(\frac{h}{2 \pi}\)

The above equation allows the possibility that if ∆x is zero; then ∆p must be infinite in order that the product is nonzero. Similarly, if ∆p is zero, ∆x must be infinite.

The wave packet description of an electron:

The above wave packet description of matter wave corresponds to an uncertainty in position (∆x) and an uncertainty in momentum (∆p).

Wave packet description for ∆p = 0:

The above wavepacket description of matter wave corresponds to a definite momentum of an electron extends all over space. In this case, ∆p = 0 and
∆x → ∞

Davisson Germer Experiment

Aim: To confirm the wave nature of electron.
Experimental setup:
The Davisson and Germer Experiment consists of filament ‘F’, which is connected to a low tension battery. The Anode Plate (A) is used to accelerate the beam of electrons. A high voltage is applied in between A and C. ’N’ is a nickel crystal. D is an electron detector. It can be rotated on a circular scale. Detector produces current according to the intensity of incident beam.

Working:
The electron beam is produced by passing current through filament F. The electron beam is accelerated by applying a voltage in between A (anode) and C. The accelerated electron beam is made to fall on the nickel crystal.

The nickel crystal scatters the electron beam to different angles. The crystal is fixed at an angle of Φ = 50° to the incident beam.

The detector current for different values of the accelerating potential ‘V’ is measured. A graph between detector current and voltage (accelerating) is plotted. The shape of the graph is shown in figure.

Analysis of graph:

The graph shows that the detector current increases with accelerating voltage and attains maximum value at 54V and then decreases. The maximum value of current at 54 V is due to the constructive interference of scattered waves from nickel crystal (from different planes of crystal). Thus wave nature of electron is established.

Experimental wavelength of electron:
The wave length of the electron can be found from the formula
2d sinθ = nλ ______(1)
From the figure, we get
θ + Φ + θ = 180°
2θ = 180 – Φ, 2θ = 180 – 50°
θ = 65°
for n = 1
equation (1) becomes
λ = 2dsinθ_____(2)
for Ni crystal, d = 0.91 A°
Substituting this in eq. (2), we get
wavelength λ = 1.65 A°
Theoretical wave length of electron:
The accelerating voltage is 54 V
Energy of electron E = 54 × 1.6 × 10¹⁹J
∴ Momentum of electron P = \(\sqrt{2 \mathrm{mE}}\)

= 39.65 × 10^-25 Kg ms^-1
∴ De-Broglie wavelength λ = \(\frac{h}{P}\)

Discussion:
The experimentally measured wavelength is found in agreement with de-Broglie wavelength. Thus wave nature of electron is confirmed.

We hope the Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter help you. If you have any query regarding Plus Two Physics Notes Chapter 11 Dual Nature of Radiation and Matter, drop a comment below and we will get back to you at the earliest.

Plus Two Physics Notes Chapter 10 Wave Optic is part of Plus Two Physics Notes. Here we have given Plus Two Physics Notes Chapter 10 Wave Optic.

Kerala Plus Two Physics Notes Chapter 10 Wave Optic

Introduction
In 1678, the Dutch physicist Christian Huygens put forward the wave theory of light. We will discuss in this chapter.

Wavefront:
The wavefront is defined as the locus of all points which have the same phase of vibration. The rays of light are normal to the wavefront. Wavefront can be divided into 3.

1. Spherical wavefront
2. Cylindrical wavefront
3. Plane wavefront.

1. Spherical Wavefront:

The wavefront originating from a point source is spherical wavefront.

2. Cylindrical Wavefront:

If the source is linear, the wavefront is cylindrical.

3. Plane wavefront:
If the source is at infinity, we get plane wavefront.

Huygen’s Principle
According to Huygen’s principle

1. Every point in a wavefront acts as a source of secondary wavelets.
2. The secondary wavelets travel with the same velocity as the original value.
3. The envelope of all these secondary wavelets gives a new wavefront.

Refraction And Reflection Of Plane Waves Using Huygens Principle
1. Refraction of a plane wave. (To prove Snell’s law):
AB is the incident wavefront and c₁ is the velocity of the wavefront in the first medium. CD is the refracted wavefront and c₂ is the velocity of the wavefront in the second medium. AC is a plane separating the two media.

The time taken for the ray to travel from P to R is

O is an arbitrary point. Hence AO is a variable. But the time to travel a wavefront from AB to CD is constant. In order to satisfy this condition, the term containing AO in eq.(2) should be zero.

where ¹n₂ is the refractive index of the second medium w.r.t. the first. This is the law of refraction.

2. Reflection of plane wave by a plane surface:

AB is the incident wavefront and CD is the reflected wavefront, ‘i’ is the angle of incidence and ‘r’ is the angle of reflection. Let c₁ be the velocity of light in the medium. Let PO be the incident ray and OQ be the reflected ray.
The time taken for the ray to travel from P to Q is

O is an arbitrary point. Hence AO is a variable. But the time to travel for a wave front from AB to CD is a constant. So eq.(2) should be independent of AO. i.e., the term containing AO in eq.(2) should be zero. AO
∴ \(\frac{A O}{C_{1}}\)(sin i – sin r) = 0
sin i – sin r= 0
sin i = sin r
i = r
This is the law of reflection.
Behavior of wave frond as they undergo refraction or reflection.

a. Wave frond through the prism:

Consider a plane wave passing through a thin prism. The speed of light waves is less in glass. Hence the lower portion of the incoming wave frond will get delayed. So outgoing wavefrond will be tilted as shown in the figure.

b. Wave frond through a thin convex lens:

Consider a plane wave passing through a thin convex lens. The central part of the incident plane wave travels through the thickest portion of lens.

Hence central part get delayed. As a result the emerging wavefrond has a depression at the centre. Therefore the wave front becomes spherical and converges to a point F.

c. Plane wave incident on a concave mirror:

A plane wave is incident on a concave mirror and on reflection we have spherical wave converging to the focul point F.

3. The Doppler Effect:
There is an apparent change in the frequency of light when the source or observer moves with respect to one another. This phenomenon is known as Doppler effect in light.

When the source moves away from the observer the wavelength as measured by the source will be larger. The increase in wavelength due to Doppler effect is called as red shift.

When waves are received from a source moving towards the observer, there is an apparent decrease in wavelength, this is referred to as blue shift.

Mathematical expression for Doppler shift:
The Doppler shift can be expressed as

V_radial is the component of source velocity along the line joining the observer to the source.

Coherent And Incoherent Addition Of Waves
Superposition principle:
According to the superposition principle, the resultant displacement produced by a number of waves at a particular point in the medium is the vector sum of the displacements produced by each of the waves.

Coherent sources:
Two sources are said to be coherent, if the phase difference between the displacements produced by each of the waves does not change with time.

Incoherent sources:
Two sources are said to be coherent, if the phase difference between the displacements produced by each of the waves changes with time.

Constructive interference:
Consider two light waves meet together at a point. If we get maximum displacement at the point of meeting, we call it as constructive interference.

Destructive interference:
Consider two lightwaves meet together at a point. If we get minimum displacement at the point of meeting, we call it as destructive interference.

Mathematical condition for Constructive interference and Destructive interference:

Consider two sources S₁ and S₂. Let P be point in the region of s₁ and s₂. The displacement produced by the source s₁ at P.
y₁ = a cos ωt
Similarly, the displacement produced by the source s₂ at P
y₂ = a cos (ωt + Φ)
Where Φ is the phase difference between the displacements produced by s₁ and s₂
The resultant displacement at P,
Y = y₁ + y₂
= a cos ωt + a cos (ωt + Φ)
= a (cos ωt + cos (ωt + Φ))

Therefore total intensity at P,

Constructive interference:
If we take phase difference Φ = 0, ±2π, ±4π……., we get maximum intensity (4I₀) at P. This is the mathematical condition for constructive interference. The condition for constructive interference can be written in the form of path difference between two waves.

Where n = 0, 1, 2, 3……..

Destructive interference:
If we take phase difference Φ = ±π, ±3π, ±5π………., we get zero intensity at P. This is the mathematical condition for destructive interference. The condition for destructive interference can be written in the form of path difference between two waves.

Where n = 0, 1, 2, 3……..

Interference Of Light Waves And Youngs Double Slit Experiment
Young’s double-slit experiment:

The experiment consists of a slit ‘S’. A monochromatic light illuminates this slit. S₁ and S₂ are two slits in front of the slit ‘S’. A screen is placed at a suitable distance from S₁ and S₂. Light from S₁ and S₂ falls on the screen. On the screen interference bands can be seen.

Explanation:
If crests (ortroughs) from S₁ and S₂ meet at certain points on the screen, the interference of these points will be constructive and we get bright bands on the screen.

At certain points on the screen, crest and trough meet together. Destructive interference takes place at those points. So we get dark bands.

Expression for band width:

S₁ and S₂ are two coherent sources having wave length λ. Let ‘d’ be the distance between two coherent sources. A screen is placed at a distance D from sources. ‘O’ is a point on the screen equidistant from S₁ and S₂.
Hence the path difference, S₁O – S₂O = 0
So at ‘O’ maximum brightness is obtained.
Let ‘P’ be the position of n^th bright band at a distance x_n from O. Draw S₁A and S₂B as shown in figure. From the right angle ∆S₁AP
we get, S₁P² = S₁A² + AP²
S₁P² = D² + (X_n – d/2)² = D² + X_n² – X_nd + \(\frac{d^{4}}{4}\)
Similarly from ∆S₂BP we get,
S₂P² = S₂B² + BP²
S₂P² = D² + (X_n + d/2)²

S₂P² – S₁P² = 2x_nd
(S₂P + S₁P)(S₂P – S₁P) = 2x_nd
But S₁P ≈ S₂P ≈ D
∴ 2D(S₂P – S₁P) = 2x_nd
i.e., path difference S₂P – S₁P = \(\frac{x_{n} d}{D}\) ____(1)
But we know constructive interference takes place at P, So we can take
(S₂P – S₁P) = nλ
Hence eq(1) can be written as

Let x_n+1 be the distance of (n+1)^th bright band from centre o, then we can write

This is the width of the bright band. It is the same for the dark band also.

Diffraction
The bending of light round the comers of the obstacles is called diffraction of light.

1. The single slit diffraction:

Consider a single slit AC having length ‘a’. A screen is placed at suitable distance from slit. B is midpoint of slit, A straight line through B (perpendicular to the plane of slit), meets the screen at O. AD is perpendicular CP.

Calculation of path difference:
Consider a point P on the screen having a angle θ with normal AE. The path difference between the rays (coming from the bottom and top of the slit) reaching at P,
CP – AP = CD
(CP – AP) = a sin θ
path difference, (CP – AP) = a θ______(1)
[for small θ. sin θ ≈ θ]

(I) Position of maximum intensity:
Consider the point ‘O’, the path difference between the rays (coming from AB and BC) reaching at O is zero. Hence constructive interference takes place at ‘O’. Thus maximum intensity is obtained. This point is called central maximum or the principal maximum.

(II) Position of secondary minima:
Let P be a point on the screen such that the path difference between the rays AP and CP be λ.
ie, CP – AP = λ______(2)
Substituting eq (1) in eq (2) we get
θ = λ
(or) θ = \(\frac{\lambda}{a}\)______(3)
Let the slit AC be imagined to be split into two equal halves AB and BC. For every point in AB, there is a corresponding point in BC such hat the distance between the points are equal to a/2 Consider two points K and L such that, KL = a/2. There fore, the path difference between the rays (coming form K and L) at P is,.
LP – KP = \(\frac{a}{2}\)θ_______(4)
Substituting (3) in (4) we get

This means that the rays (coming from K and L) reaching at P are out of phase and cancel each other. Hence the intensity at P becomes zero.
In otherwards, at angle θ = \(\frac{\lambda}{\mathrm{a}}\)
The intensity becomes zero.
Similarly on the lower half of the screen, the intensity is zero for which θ = – \(\frac{\lambda}{\mathrm{a}}\)
The general equation for zero intensity can be written as
θ = \(\pm \frac{n \lambda}{a}\)
Where n = 1, 2, 3,…
For first minima n = 1, and second minima n = 2.

(III) Position of Secondary maxima:
Let P be a point on the screen, such that
CP – AP = \(\frac{3}{2}\)λ
From eq (1),we know (CP – AP) = aθ
Therefore aθ = \(\frac{3}{2}\)λ
The wave front AC can be divided into three equal parts.

The rays from first and second parts will cancel each other and the rays from third part will reach at P. Hence the point P becomes bright.

Similarly the next maximum occurs at θ = \(\frac{5}{2}\)\(\frac{λ}{a}\)
The general equation for maximum can be written
\(\theta=\pm \frac{(2 n+1) \lambda}{2 a}\)

1. (a) Intensity Distribution on the screen of diffraction pattern:

(b) Comparison between interference and diffraction bands:
Interference:

• Interference is due to superposition of waves coming from two wavefronts.
• Interference bands are of equal width.
• Minimum intensity regions are perfectly dark.
• All the bright bands are of equal intensity.

Diffraction:

• Diffraction is due to the superposition of waves coming from different parts of the same wave front.
• Diffraction bands are of unequal width.
• Minimum intensity regions are not perfectly dark.
• All bright bands are not of the same intensity.

2. Seeing The Single Slit Diffraction Pattern:

Take two razor blades and an electric bulb. Hold the two blades as shown in the figure. Observe the glowing bulb through the slit. A diffraction pattern can be seen.

3. Resolving Power Of Optical Instruments:
Resolving power of optical instrument:
The ability of an optical instrument to form distinctly separate images of the two closely placed objects is called is resolving power.

Explanation:

The image of a point object formed by an ideal lens is a point only. But because of diffraction effect, instead of point image, we get a diffraction pattern. Diffraction pattern consists of a bright central circular region surrounded by concentric dark and light rings.

Let us discuss three cases; when we observe two-point object through a lens.

1. Unresolved:
If central maxima of two diffraction pattern are overlapped, the image is unresolved. This image can’t be viewed clearly.

2. Just resolved:
If central maxima of two diffraction pattern are just separated, the image is just resolved. In this case image is just distinqushed.

3. Resolved:
If central maxima of two diffraction pattern are separated, the image is resolved. This image can be viewed clearly.

Limit of resolving power of optical instrument:
The minimum distance of separation between two points so that they are just resolved by the optical instrument is known as its limit of resolution. Resolving power is also defined as reciprocal of limit of resolution.

1. Telescope and resolving power:

Telescope consist of two convex lenses called eyepiece and objective .The light falling on objective lens undergoes for diffraction. Hence a diffraction pattern of bright and dark rings is produced around central bright region as shown in figure.
The radius of central bright region,

This radius can be written in terms of angular width,
∆θ ≈ \(\frac{0.61 \lambda}{\mathrm{a}}\)
Where a is the radius and f – focal length of objective lens. λ is the wave length of light used.

This angular width of central bright region is related to resolving power of telescope. When angular width of spot increases, resolving power decreases.

The limit of resolution of telescope, ∆θ ≈ \(\frac{0.61 \lambda}{\mathrm{a}}\)
This equation shows that telescope will have better resolving power if ‘a’ is large and λ is small.

2. Microscope and resolving power:

In microscope the object (microscopic size) is placed slightly beyond f (focal length of objective lens). When the separation between two points in a microscopic specimen is comparable to the wavelength λ of light, the diffraction effect become important.

Where nsinβ is called numerical aperture, n is the refractive index of liquid used in microscope, β is the half angle of the cone of light from the microscopic object with objective lens.
The limit of resolution of microscope d_min = \(\frac{1.22 f \lambda}{2 n \sin \beta}\)
This equation also can be written as d_min = \(\frac{1.22 \lambda}{2 \tan \beta}\)

Note: Telescope is used to resolve objects at far distance but microscope is used to produce magnification of near objects.

4. The Validity Of Ray Optics:
Fresnel distance is the distance beyond which the diffraction properties becomes significant, (ie. the ray optics is converted into wave optics).
Fresnel distance, z_F = \(\frac{\mathrm{a}^{2}}{\lambda}\)
Where ‘a’ is the size of the aperture
For distances much smaller than z_F, the spreading due to diffraction is smaller compared to the size of the beam. It becomes comparable when the distance is approximately z_F. For distances much greater than z_F, the spreading due to diffraction dominates over that due to ray optics.

Polarisation

Consider a long string that is held horizontally, the other end of which is assumed to be fixed. If we move the end of the string up and down in a periodic manner, a wave will propagate in the +xdirection (see above figure). Such a wave can be described by the following equation
y(x,t) = a sin (kx – ωt)
where ‘a’ represent the amplitude and k = 2π/λ represents the wavelength associated with the wave.

Since the displacement (which is along the y-direction) is at right angles to the direction of propagation of the wave, this wave is known as a transverse wave.

Also, since the displacement is in the/direction, it is often called to as a y-polarised wave. Since each point on the string moves on a straight line, the wave is also called to as a linearly polarised wave.

The string always remains confined to the x-y plane and therefore it is also called to as a plane polarised wave.

In a similar manner we can consider the vibration of the string in the x-z plane generating a z-polarised wave whose displacement will be given by
z(x,t) = a sin (kx – ωt)

Unpolorised wave:
If the plane of vibration of the string is changed randomly in very short intervals of time, then it is known as an unpolarized wave.

(a) Polarization property of light:
When light passes through certain crystals like tourmaline, the vibrations of electric field vector are restricted. This property exhibited by light is known as polarization.

Note:

1. Polarization is the property of light which reveals that light is a transverse wave.
2. A sound wave can’t be polarized because sound wave is a longitudinal wave.

Polarizer and analyzer:
When an unpolarized light passes through a tourmaline crystal T₁, the light coming out of T₁ is plane polarized.

In order to check the polarization, another tourmaline crystal T₂ is kept parallel to T₁.

When we look through T₂ we get maximum intensity. Then T₂ is rotated through 90°. If no light is coming, we can say that light from T₁ is plane polarized.

Polarizer: The crystal which produces polarized light is known as polarizer.

Analyzer: The crystal which is used to check weather the light is polarized or not is called the analyzer or detector.

Law of Malus: This law states that when a beam of plane polarized light is incident on an analyzer, the intensity (I) of the emergent light is directly proportional to the square of the cosine of the angle (θ) between the polarizing directions of the polarizer and the analyzer.

I = I_m cos²θ
where I_m is the maximum intensity.

1. Polarisation By Scattering:

The nunpolarized light incident on a dust particle in atmosphere, it is absorbed by electrons in the dust particle. The electrons in the dust particle reradiate light in all directions. This phenomenon is called scattering.

Explanation:
Let a beam of unpolarized light be incident on a dust particle along x-axis. The electrons in the dust particle absorb light and behave as a oscillating dipole. This dipole emit light in all directions.

When an observer observe this particle along y-axis, the observer can receive light from the electron vibrating in z-axis. This light is linearly polarised in z-direction (its plane of polarisation is yz).

This polarised light is represented by dots in the picture. This explains the polarisation of scattered light from the sky.

2. Polarization By Reflection:
At a particular angle of incidence on a medium, the reflected lights is fully polarized. This angle is known as polarizing angle or Brewster’s angle. At polarizing angle, the reflected and refracted rays are mutually perpendicular.

Brewster’s law:
Brewster’s law states that the tangent of the polarizing angle is equal to the refractive index of the material of the reflector.

Let ‘Q ’ be the polarizing angle and ‘n’ be the refractive index of the medium then,
tan θ = n
At polarizing angle, r + θ =90°.

Proof:
Consider an unpolarized light coming from air and is incident on a medium having refractive index n. Let θ be the angle of incidence, Φ be the angle of reflection and ‘r’ be the angle of refraction.
Using snells law, we can write
n = \(=\frac{\sin \theta}{\sin r}\) ______(1)
At the polarizing angle reflected and refracted light are mutually perpendicular
ie. Φ – 90 + r = 180°
∴ r = 90 – Φ______(2)
Substituting eq (2) in eq(1), we get

But we know
Angle of incidence (θ) = angle of reflection(Φ)
∴ n = \(\frac{\sin \theta}{\cos \theta}\)
n = tanθ

We hope the Plus Two Physics Notes Chapter 10 Wave Optic help you. If you have any query regarding Plus Two Physics Notes Chapter 10 Wave Optic, drop a comment below and we will get back to you at the earliest.