Tangents and Circles
A tangent to a circle is a line in the plane of the circle that intersects the circle in exactly one point.
If you spin an object in a circular orbit and release it, it will travel on a path that is tangent to the circular orbit.
Theorem:
If a line is tangent to a circle, it is perpendicular to the radius drawn to the point of tangency.
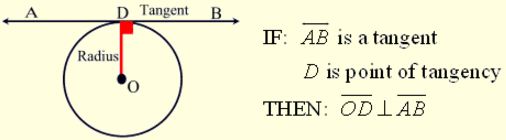Theorem:
Tangent segments to a circle from the same external point are congruent.
(You may think of this as the “Hat” Theorem because the diagram looks like a circle wearing a pointed hat.)
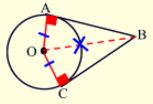
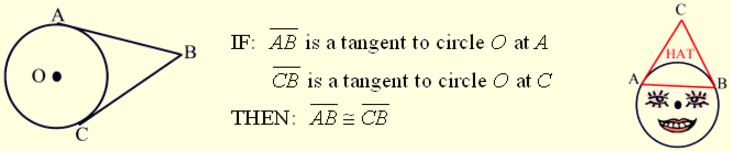This theorem can be proven using congruent triangles and the previous theorem. The triangles shown below are congruent by the Hypotenuse Leg Postulate for Right Triangles. The radii (legs) are congruent and the hypotenuse is shared by both triangles. By using Corresponding Parts of Congruent Triangles are Congruent, this theorem is proven true.
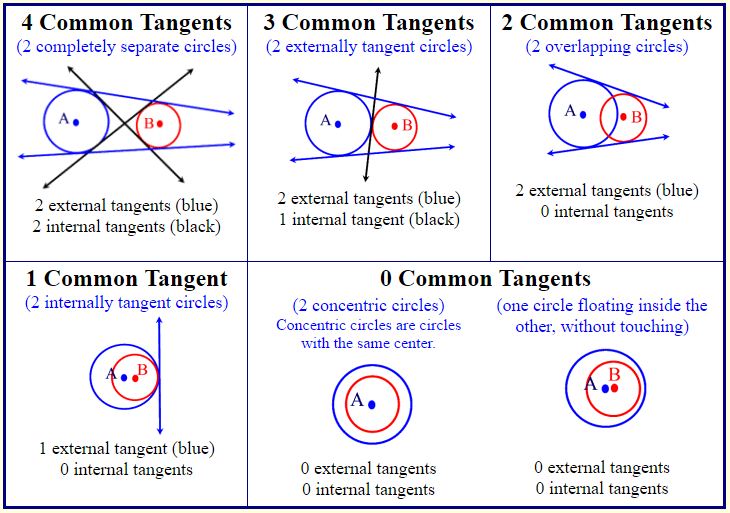
Common Tangents:
Common tangents are lines or segments that are tangent to more than one circle at the same time.
