What is a Proof
A proof is a written account of the complete thought process that is used to reach a conclusion. Each step of the process is supported by a theorem, postulate or definition verifying why the step is possible.
In formal Euclidean proofs, no steps can be left out.
If you think about the numerical problems you are used to solving in geometry, you will realize that your mind often does a “fast-forward” through some of the logical steps needed to reach a valid answer. In other words, you quickly “go right to the answer.”
Check out the numerical problem below:
You probably arrived at the answer of 6 long before you finished reading the explanation of the answer. Right?
When developing a proof of this same problem, we must be careful to include ALL of the steps that led to our answer. We cannot “fast-forward” over steps when writing a proof. Check out the “proof” of this same problem:
A proof requires that you document all of the little steps that you mentally “fast-forwarded” through in the numerical problem.
What’s in a proof?
A formal 2-column proof contains the following components:
- Statement of the original problem
Example:
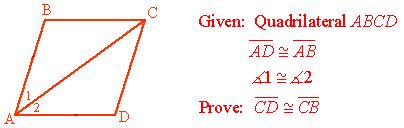
This information is usually stated in the original problem. Some word problems, however, have to be dissected in order to get the specific information needed for the proof. - Diagram, marked with “Given” information
Example:
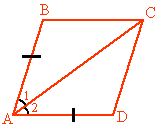
The diagram usually is not marked, so this step is very important. You will see the sought after congruent triangles and their corresponding parts much clearer with the diagram marked. - Re-statement of the “Given” information in the proof
Example:
\(\overline { AD }\) ≅ \(\overline { AB }\), ∡1≅ ∡2
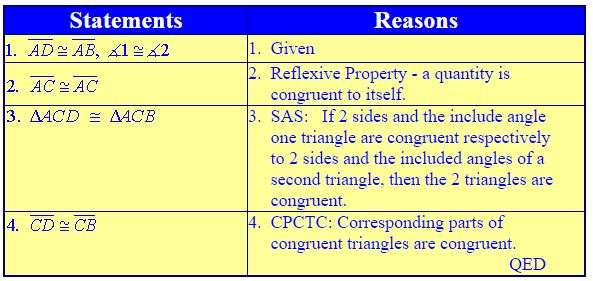
Stating of the “given” information is almost always the first statement, and the reason is simply GIVEN. - Complete supporting reasons for each step in the proof
Example:
1. Given
2. Reflexive Property
3. SAS: If 2 sides and the include angle one triangle are congruent respectively to 2 sides and the included angles of a second triangle, then the 2 triangles are congruent.
4. Corresponding parts of congruent triangles are congruent.
These supporting “reasons” vary between textbooks (and teachers), so be careful to follow the guidelines set by your teacher. - The “Prove” statement as the last statement
Example:
\(\overline { CD }\) ≅ \(\overline { CB }\)
The “PROVE” is always the final statement. This statement is the purpose for the entire problem.
A Successful Strategy: Backwards Looking
For most proof problems, it is very helpful to examine the problem backwards — from the “Prove” statement back to the “Given” information. Let’s look at an example:
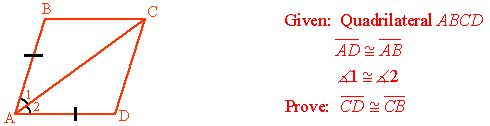
A Backwards Look — Where does the conclusion come from?
By looking at the above steps, we can see how to proceed with the proof. You might want to consider jotting down your “backward” thoughts before you begin writing your proof.
