Plus Two Maths Chapter Wise Questions and Answers Chapter 3 Matrices are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 3 Matrices.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 3 |
| Chapter Name | Matrices |
| Number of Questions Solved | 39 |
| Category | Plus Two Kerala |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 3 Matrices
Plus Two Maths Matrices Three Mark Questions and Answers
Question 1.
Find the value of a, b and c from the following equations;
\(\left[\begin{array}{cc}{a-b} & {2 a+c} \\{2 a-b} & {3 c+d}
\end{array}\right]=\left[\begin{array}{cc}{-1} & {5} \\{0} & {13}\end{array}\right]\).
Answer:
Given;
\(\left[\begin{array}{cc}{a-b} & {2 a+c} \\{2 a-b} & {3 c+d}
\end{array}\right]=\left[\begin{array}{cc}{-1} & {5} \\{0} & {13}\end{array}\right]\)
⇒ a – b = -1, 2a + c = 5, 2a – b = 0, 3c + d = 13
⇒ a – b = -1
2a – b = 0
– a = -1
⇒ a = 1
We have, a – b = -1 ⇒ 1 – b = -1 ⇒ b = 2
⇒ 2a + c = 5 ⇒ 2 + c = 5 ⇒ c = 3
⇒ 3c + d = 13 ⇒ 9 + d = 13 ⇒ d = 4.
Question 2.
Simplify cosx\(\left[\begin{array}{cc}{\cos x} & {\sin x} \\{-\sin x} & {\cos x}\end{array}\right]\) + sinx\(\left[\begin{array}{cc}{\sin x} & {-\cos x} \\{\cos x} & {\sin x}\end{array}\right]\).
Answer:
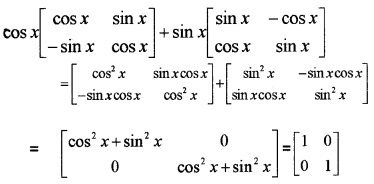
Question 3.
Solve the equation for x, y z and t; if
\(2\left[\begin{array}{ll}{x} & {z} \\{y} & {t}\end{array}\right]+3\left[\begin{array}{cc}{1} & {-1} \\{0} & {2}\end{array}\right]=3\left[\begin{array}{ll}{3} & {5} \\{4} & {6}\end{array}\right]\).
Answer:
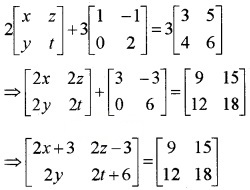
⇒ 2x + 3 = 9 ⇒ x = 3
⇒ 2z – 3 = 15 ⇒ z = 9
⇒ 2y = 12 ⇒ y = 6
⇒ 2t + 6 = 18 ⇒ t = 6.
Question 4.
Find A2 – 5A + 6I If A = \(\left[\begin{array}{ccc}{2} & {0} & {1} \\{2} & {1} & {3} \\{1} & {-1} & {0}\end{array}\right]\)
Answer:
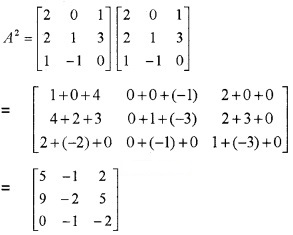
A2 – 5A + 6I
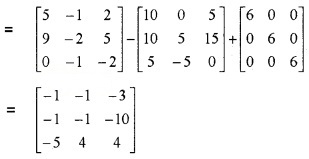
Question 5.
If A = \(\left[\begin{array}{cc}{3} & {-2} \\{4} & {-2}\end{array}\right]\) find k so that A2 = kA – 2I.
Answer:
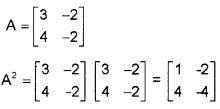
Given A2 = kA – 2I
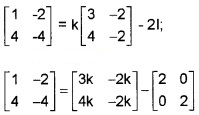
1 = 3k – 2
⇒ k = 1.
Question 6.
Express A = \(\left[\begin{array}{ccc}{-1} & {2} & {3} \\{5} & {7} & {9} \\{-2} & {1} & {1}
\end{array}\right]\) as the sum of a symmetric and skew symmetric matrix.
Answer:

P = 1/2 (A + AT) is symmetric.
Q = 1/2 (A – AT) is skew symmetric.
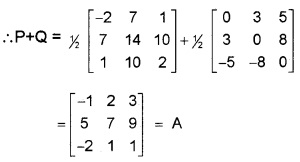
Question 7.
Find the inverse of the following using elementary transformations.
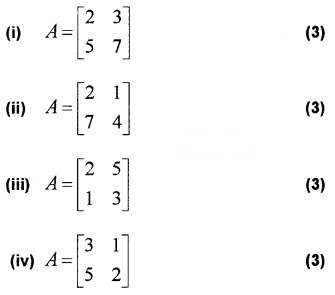
Answer:
(i) Let A = I A
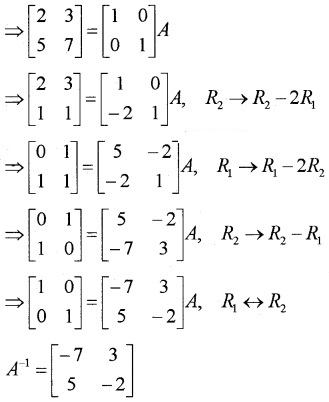
(ii) Let A = IA
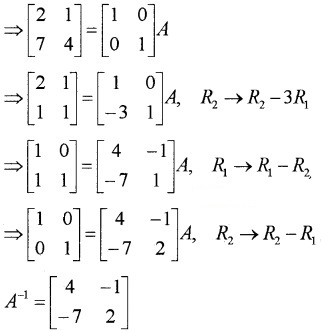
(iii) Let A = IA
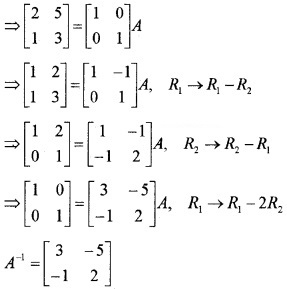
(iv) Let A = IA
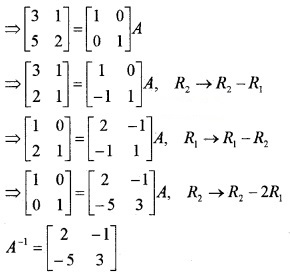
Question 8.
Find the inverse of the matrix A = \(\left[\begin{array}{cc}{2} & {3} \\{-1} & {5}\end{array}\right]\) using row transformation.
Answer:
A = \(\left[\begin{array}{cc}{2} & {3} \\{-1} & {5}\end{array}\right]\)
Let A = IA

Question 9.
\(A=\left[\begin{array}{ll}{2} & {3} \\{4} & {5} \\{2} & {1}\end{array}\right] B=\left[\begin{array}{ccc}{1} & {-2} & {3} \\{-4} & {2} & {5}\end{array}\right]\)
- Find AB
- If C is the matrix obtained from A by the transformation R1 → 2R1, find CB
Answer:
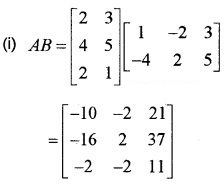
(ii) Since C is the matrix obtained from A by the transformation R1 → 2R1
⇒ C = \(\left[\begin{array}{ll}{4} & {6} \\{4} & {5} \\{2} & {1}\end{array}\right]\)
Then CB can be obtained by multiplying first row of AB by 2.
CB = \(\left[\begin{array}{ccc}{-20} & {-4} & {42} \\{-16} & {2} & {37} \\{-2} & {-2} & {11}
\end{array}\right]\).
Question 10.
Construct a 3 × 4 matrix whose elements are given by
- ay = \(\frac{|-3 i+j|}{2}\) (2)
- aij = 2i – j (2)
Answer:
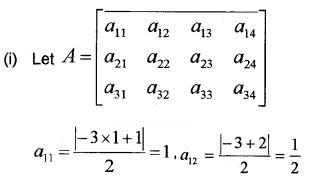
a13 = 0, a14 = \(\frac{1}{2}\), a21 = \(\frac{5}{2}\), a22 = 2, a23 = \(\frac{3}{2}\), a24 = 1, a31 = 4, a32 = \(\frac{7}{2}\), a33 = 3, a34 = \(\frac{5}{2}\)
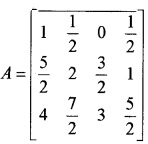
a11 = 1, a12 = 0, a13= -1, a14 = -2, a21 = 3, a22 = 2, a23 = 1, a24 = 0, a31 = 5, a32 = 4, a33 = 3, a34 = 2
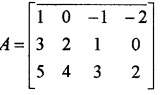
Question 11.
Express the following matrices as the sum of a Symmetric and a Skew Symmetric matrix.
(i) \(\left[\begin{array}{ccc}{6} & {-2} & {2} \\{-2} & {3} & {-1} \\{2} & {-1} & {3}
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}{3} & {3} & {-1} \\{-2} & {-2} & {1} \\{-4} & {-5} & {2}
\end{array}\right]\)
Answer:

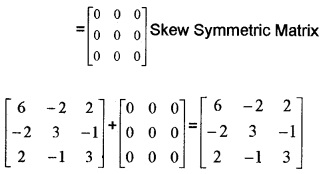
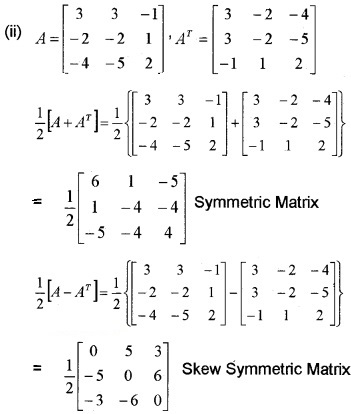
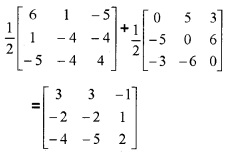
Question 12.
If A = \(\left[\begin{array}{ccc}{2} & {4} & {3} \\{1} & {0} & {6} \\{0} & {-2} & {-3}\end{array}\right]\)
- Find 3A. (1)
- Find AT (1)
- Evaluate A + AT , is it symmetric? Justify your answer. (1)
Answer:
1. 3A = \(\left[\begin{array}{ccc}{6} & {12} & {9} \\{3} & {0} & {18} \\{0} & {-6} & {-9}
\end{array}\right]\)
2. AT = \(\left[\begin{array}{ccc}{2} & {1} & {0} \\{4} & {0} & {-2} \\{3} & {6} & {-3}
\end{array}\right]\)
3. A + AT

The elements on both sides of the main diagonal are same. Therefore A + AT is a symmetric matrix.
Plus Two Maths Matrices Four Mark Questions and Answers
Question 1.
Consider the following statement: P(n) : An = \(\left[\begin{array}{cc}{1+2 n} & {-4 n} \\{n} & {1-2 n}\end{array}\right]\) for all n ∈ N
- Write P (1). (1)
- If P(k) is true, then show that P( k + 1) is also true. (3)
Answer:
1. P(1) : A = \(\left[\begin{array}{cc}{1+2} & {-4} \\{1} & {1-2}\end{array}\right]=\left[\begin{array}{cc}{3} & {-4} \\{1} & {-1}\end{array}\right]\)
2. Assume that P(n) is true n = k
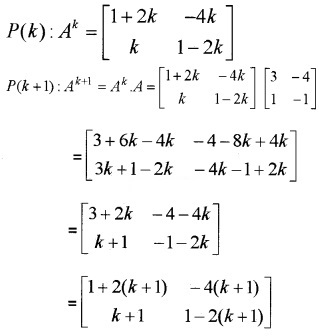
Hence P(k+1) is true n ∈ N.
Question 2.
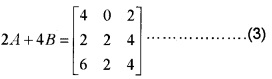
Find the matrices A and B if 2A + 3B = \(\left[\begin{array}{ccc}{1} & {2} & {-1} \\{0{1} & {2} & {4}\end{array}\right]\) and A + 2B = \(\left[\begin{array}{lll}{2} & {0} & {1} \\{1} & {1} & {2} \\{3} & {1} & {2}\end{array}\right]\).
Answer:
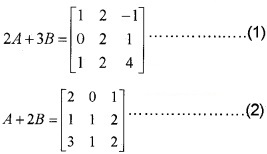
Solving (1) and (2) ⇒ 2 × (2)

Question 3.
- Construct a 3 × 3 matrix A = [aij] where aij – 2(i – j) (3)
- Show that matrix A is skew-symmetric. (1)
Answer:
1.
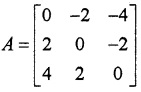
2.

Therefore A is a skew-symmetric matrix.
Question 4.
Consider the following statement P(n ): An = \(\left[\begin{array}{cc}{\cos n \theta} & {\sin n \theta} \\{-\sin n \theta} & {\cos n \theta}\end{array}\right]\) for all n ∈ N
- Write P(1). (1)
- If P (k) is true then show that P (k+1) is true (3)
Answer:
1.
2. Assume that P(n) is true for n = k
P(k+1) = Ak+1
∴ P(k+1) is true. Hence true for all n ∈ N.
Question 5.
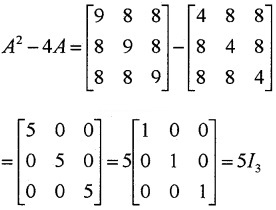
A = \(\left[\begin{array}{lll}{1} & {2} & {2} \\{2} & {1} & {2} \\{2} & {2} & {1}\end{array}\right]\), then
- Find 4A and A2 (2)
- Show that A2 -4A = 5I3 (2)
Answer:
1.
2.
Question 6.
Let A = \(\left[\begin{array}{lll}{2} & {1} & {3} \\{4} & {1} & {0}\end{array}\right]\) and B= \(\left[\begin{array}{cc}{1} & {-1} \\{0} & {2} \\{5} & {0}\end{array}\right]\)
- Find AT and BT (1)
- Find AB (1)
- Show that (AB)T = BT AT (2)
Answer:
1.
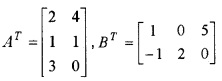
2.
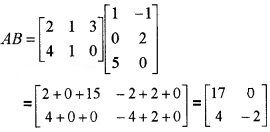
3.
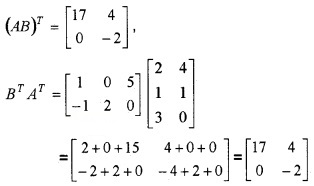
∴ (AB)T = BT AT.
Question 7.
A = \(\left[\begin{array}{ccc}{1} & {-3} & {1} \\{2} & {0} & {4} \\{1} & {2} & {-2}\end{array}\right]\) Express A as the sum of a symmetric and skew symmetric matrix.
Answer:

\(\frac{1}{2}\) (A + AT) + \(\frac{1}{2}\) (A – AT)
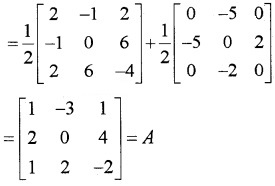
Question 8.
- Consider a 2 × 2 matrix A = [aij], where aij = \(\frac{(i+j)^{2}}{2}\)
- Write the transpose of A. (2)
- Show that A is symmetric. (2)
Answer:
1. A = \(\left[\begin{array}{ll}{2} & {\frac{9}{2}} \\{\frac{9}{2}} & {8}\end{array}\right]\)
2. AT = \(\left[\begin{array}{ll}{2} & {\frac{9}{2}} \\{\frac{9}{2}} & {8}\end{array}\right]\)
3. AT = A therefore symmetric matrix.
Question 9.
A = \(\left[\begin{array}{ll}{6} & {5} \\{7} & {6}\end{array}\right]\) is a matrix
- What is the order of A. (1)
- Find A2 and 12 A. (2)
- If f(x) = xT – 12x +1; find f(A). (1)
Answer:
1. Order of A is 2 × 2.
2.
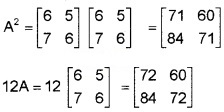
3. f(x) = x2 – 12x + 1 ⇒ f(A) = A2 – 12A + I

Plus Two Maths Matrices Six Mark Questions and Answers
Question 1.
Let A = \(\left[\begin{array}{ll}{2} & {4} \\{3} & {2}\end{array}\right]\), B = \(\left[\begin{array}{cc}{1} & {3} \\{-2} & {5}\end{array}\right]\), C = \(\left[\begin{array}{rr}{-2} & {5} \\{3} & {4}\end{array}\right]\)
Find each of the following
(i) A + B; A – B
(ii) 3A – C
(iii) AB
(iv) BA
Answer:
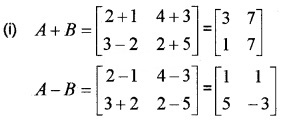
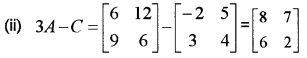
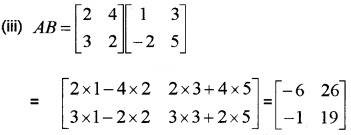
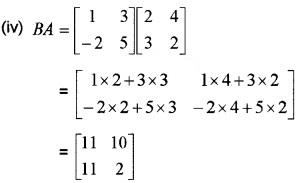
Question 2.
Let A = \(\left[\begin{array}{ll}{1} & {2} \\{3} & {4}\end{array}\right]\); B = \(\left[\begin{array}{ll}{2} & {1} \\{4} & {5}\end{array}\right]\); C = \(\left[\begin{array}{ccc}{1} & {-1} \\{0} & {2}\end{array}\right]\)
(i) Find A + B and A – B (2)
(ii) Show that (A + B) + C = A + (B + C) (2)
(iii) Find AB and BA
Answer:
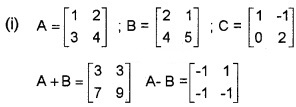
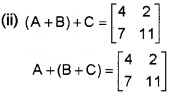
∴ (A + B) + C = A + (B + C)
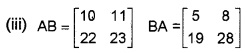
Question 3.
A = \(\left[\begin{array}{ccc}{-1} & {0} & {2} \\{4} & {0} & {-3}\end{array}\right]\), B = \(\left[\begin{array}{cc}{0} & {2} \\{-1} & {3} \\{0} & {4}\end{array}\right]\)
- What is the order of matrix AB ? (1)
- Find AT, BT (2)
- Verify (AB)T = BT AT (3)
Answer:
1. Order of AB is 2 × 2. Since order of A is 2 × 3 and B is 3 × 2.
2.
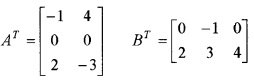
3.
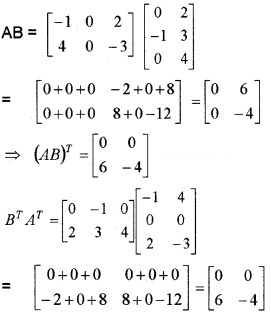
(AB)T = BT AT.
Question 4.
Let A = \(\left[\begin{array}{rrr}{1} & {2} & {-3} \\{2} & {1} & {-1}\end{array}\right]\), B = \(\left[\begin{array}{ll}{2} & {3} \\{5} & {4} \\{1} & {6}\end{array}\right]\)
(i) FindAB. (1)
(ii) Find AT, BT & (AB)T (3)
(iii) Verify that (AB)T = BT AT (2)
Answer:
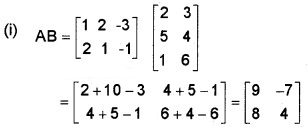
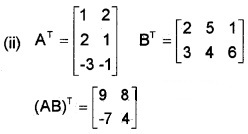
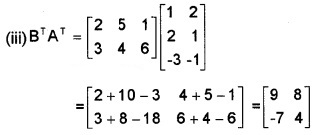
Question 5.
If A = \(\left[\begin{array}{c}{-2} \\{4} \\{5}\end{array}\right]\), B = \(\left[\begin{array}{lll}{1} & {3} & {6}\end{array}\right]\)
(i) Find AT, BT (1)
(ii) Find (AB)T (2)
(iii) Verify (AB)T = BT AT (3)
Answer:
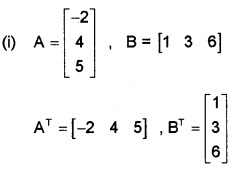

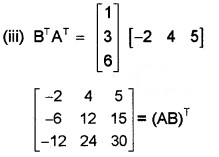
Question 6.
Let A = \(\left[\begin{array}{cc}{3} & {1} \\{-1} & {2}\end{array}\right]\)
(i) Find A2 (1)
(ii) Show that A2 – 5A + 7I = 0 (1)
(iii) Using this result find A-1 (2)
(iv) Slove the following equation using matrix: 3x + y = 1, – x + 2y = 2.
Answer:
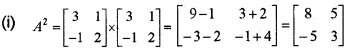
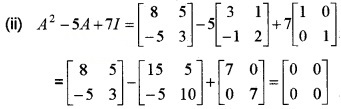
(iii) A2 – 5A + 7I = 0 ⇒ A2 – 5A = -7I,
multiplying by A-1 on both sides,
⇒ A – 5I = -7 A-1
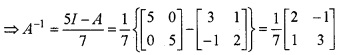
(iv) The equation can be represented in matrix form as follows, AX = B ⇒ X = A-1B
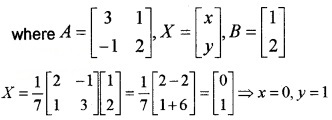
Question 7.
A = \(\left[\begin{array}{ccc}{1} & {2} & {3} \\{3} & {-2} & {1} \\{4} & {2} & {1}
\end{array}\right]\)
(i) Show that A3 – 23A – 40I = 0 (3)
(ii) Hence find A-1 (3)
Answer:
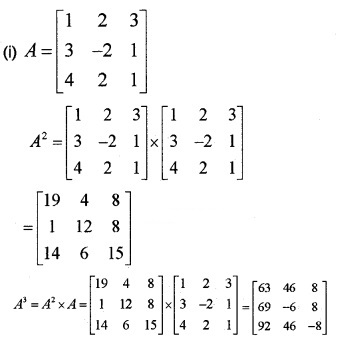
A3 – 23A – 40I = 0
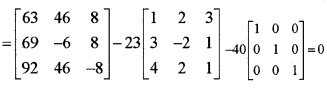
(ii) A-1A3 – 23 A-1A – 40A-1I = 0
⇒ A2 – 23I – 40A-1 = 0
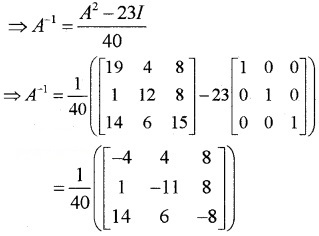
Question 8.
A is a third order square matrix and \(a_{i j}=\left\{\begin{aligned}-i+2 j & \text { if } i=j \\i \times j & \text { if } i \neq j\end{aligned} \text { and } B=\left[\begin{array}{lll}{2} & {1} & {1} \\{1} & {1} & {5} \\{1} & {5} & {2}\end{array}\right]\right.\)
- Construct the matrix A. (1)
- Interpret the matrix A. (1)
- Find AB – BA. (3)
- Interpret the matrix AB – BA. (1)
Answer:
1. a11 = 1, a12 = 2, a13 = 3, a21 = 2, a22 = 2, a23 = 6, a31 = 3, a32 = 6, a33 = 3
A = \(\left[\begin{array}{lll}{1} & {2} & {3} \\{2} & {2} & {6} \\{3} & {6} & {3}\end{array}\right]\)
2. Now,
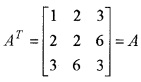
Therefore A is symmetric matrix.
3.


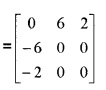
4.
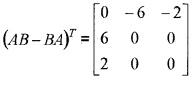
= -(AB – BA)
∴ skew symmetric matrix.
Question 9.
Find x and y if
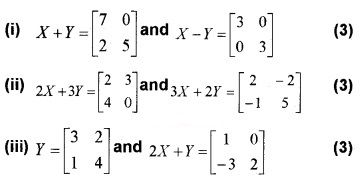
Answer:
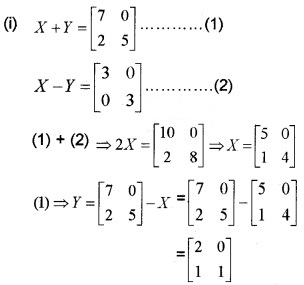
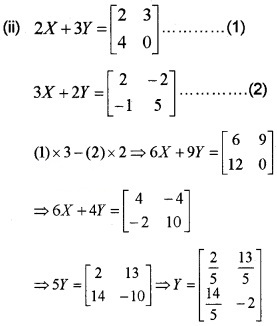
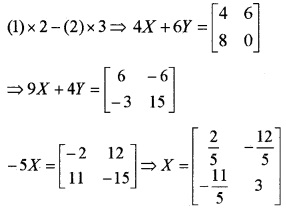
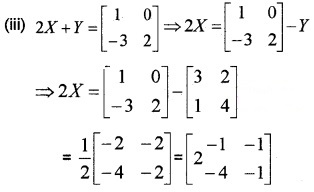
Question 10.
Given that A + B = \(\left[\begin{array}{ll}{2} & {5} \\{7} & {8}\end{array}\right]\) and A – B = \(\left[\begin{array}{ll}{6} & {8} \\{4} & {3}\end{array}\right]\)
- Find 2A. (1)
- Find A2 – B2. (3)
- Is it equal to (A + B) (A – B)? Give reason (2)
Answer:
1. 2A = A + B + A – B
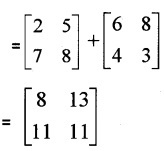
2.

3. (A + B)(A – B)
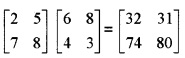
(A + B)(A – B) = A2 + AB – BA – B2
≠ A2 – B2
∵ AB ≠ BA.
Question 11.
(i) Consider A = \(\left[\begin{array}{lll}{1} & {x} & {1}\end{array}\right]\), B = \(\left[\begin{array}{ccc}{1} & {3} & {2} \\{2} & {5} & {1} \\{15} & {3} & {2}
\end{array}\right]\), C = \(\left[\begin{array}{l}{1} \\{2} \\{x}\end{array}\right]\) (2)
| A – Matrix | B – Order |
| A | 3 × 1 |
| B | 1 × 1 |
| BC | 2 × 2 |
| ABC | 3 × 3 |
| 1 × 3 |
(ii) Find x if ABC = 0 (4)
Answer:
(i)
| A – Matrix | B – Order |
| A | 1 × 3 |
| B | 3 × 3 |
| BC | 3 × 1 |
| ABC | 1 × 1 |
(ii) Given, ABC = 0
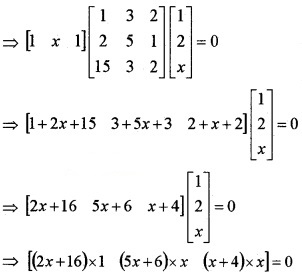
⇒ x2 + 16x + 28 = 0
⇒ (x + 14)(x + 2) = 0
⇒ x = -14, -2.
We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 3 Matrices will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 3 Matrices, drop a comment below and we will get back to you at the earliest.