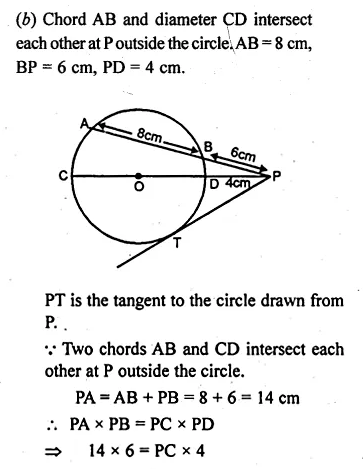
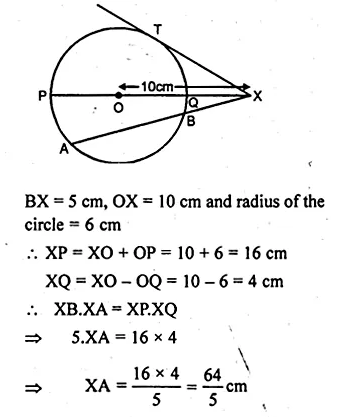
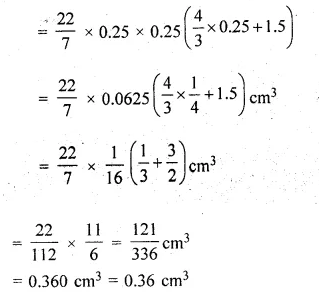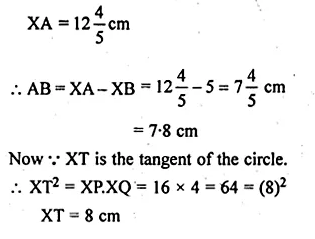ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Identities Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Identities Chapter Test.
ML Aggarwal SolutionsICSE SolutionsSelina ICSE Solutions
Question 1.
(i) If θ is an acute angle and cosec θ = √5 find the value of cot θ – cos θ.
(ii) If θ is an acute angle and tan θ = \(\\ \frac { 8 }{ 15 } \), find the value of sec θ + cosec θ.
Solution:
(i) θ is an acute angle.
cosec θ = √5
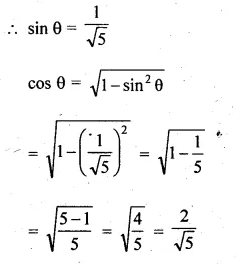
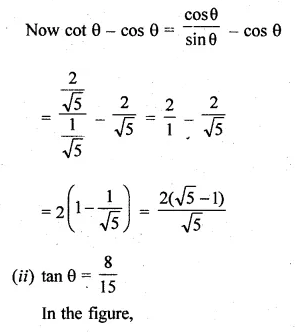
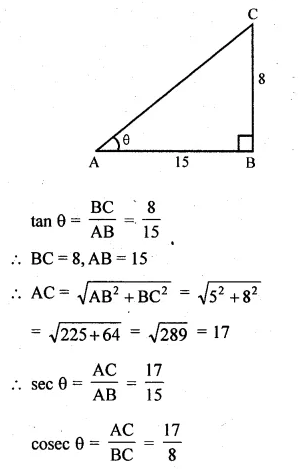
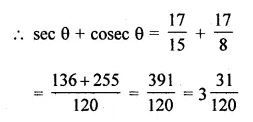
Question 2.
Evaluate the following:
(i) \(2\times \left( \frac { { cos }^{ 2 }{ 20 }^{ O }+{ cos }^{ 2 }{ 70 }^{ O } }{ { sin }^{ 2 }{ 25 }^{ O }+{ sin }^{ 2 }{ 65 }^{ O } } \right) \) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°
(ii) \(\frac { { sec }29^{ O } }{ { cosec }61^{ O } } \) + 2 cot 8° cot 17° cot 45° cot 73°0 cot 82° – 3(sin2 38° + sin2 52°)
(iii) \(\frac { { sin }^{ 2 }{ 22 }^{ O }+{ sin }^{ 2 }{ 68 }^{ O } }{ { cos }^{ 2 }{ 22 }^{ O }+{ cos }^{ 2 }{ 68 }^{ O } } \) + sin2 63° + cos 63° sin 27°
Solution:
(i) \(2\times \left( \frac { { cos }^{ 2 }{ 20 }^{ O }+{ cos }^{ 2 }{ 70 }^{ O } }{ { sin }^{ 2 }{ 25 }^{ O }+{ sin }^{ 2 }{ 65 }^{ O } } \right) \) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°
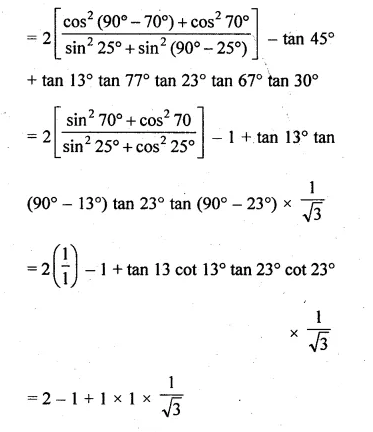
Question 3.
If \(\\ \frac { 4 }{ 3 } \) (sec2 59° – cot2 31°) – \(\\ \frac { 2 }{ 2 } \) sin 90° + 3tan2 56° tan2 34° = \(\\ \frac { x }{ 2 } \), then find the value of x.
Solution:
Given
\(\\ \frac { 4 }{ 3 } \) (sec2 59° – cot2 31°) – \(\\ \frac { 2 }{ 2 } \) sin 90° + 3tan2 56° tan2 34° = \(\\ \frac { x }{ 2 } \)
Question 4.
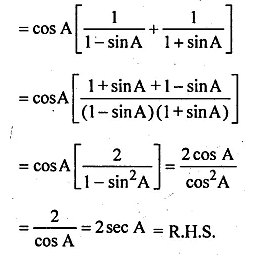
(i) \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } =2secA \)
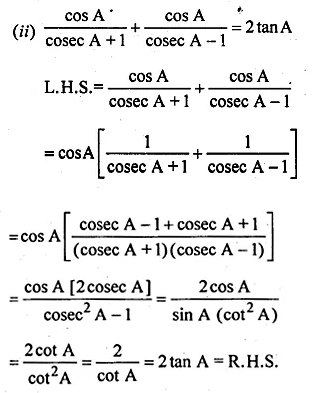
(ii) \(\frac { cosA }{ cosecA+1 } +\frac { cosA }{ cosecA-1 } =2tanA \)
Solution:
(i) \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } =2secA \)
L.H.S = \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } \)
Question 5.
(i) \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } =sec\theta \)
(ii) (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) = 1.
Solution:
(i) \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } =sec\theta \)
L.H.S = \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } \)
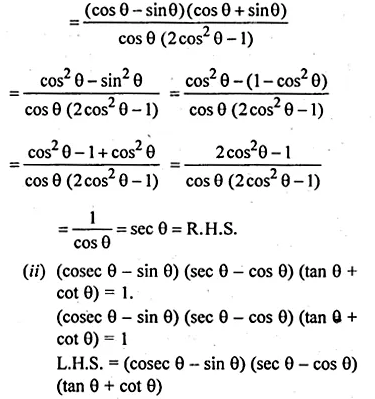
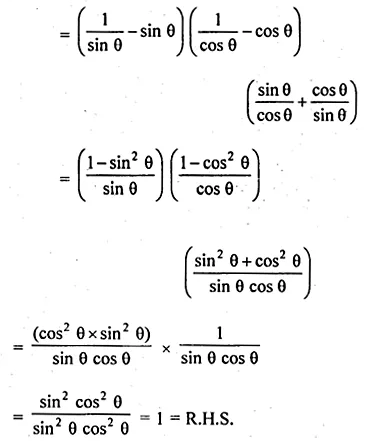
Question 6.
(i) sin2 θ + cos4 θ = cos2 θ + sin4 θ
(ii) \(\frac { cot\theta }{ cosec\theta +1 } +\frac { cosec\theta +1 }{ cot\theta } =2sec\theta \)
Solution:
L.H.S. = sin2 θ + cos4 θ
= (1 – cos2 θ + cos4 θ
= 1 – cos2 θ + cos4 θ
= 1 – cos2 θ (1 – cos2 θ)
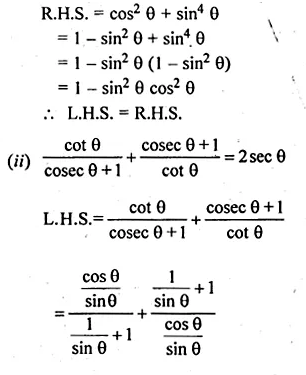
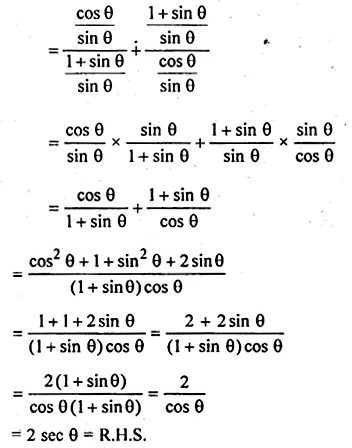
Question 7.
(i) sec4 A (1 – sin4 A) – 2 tan2 A = 1
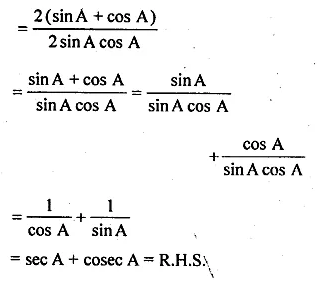
(ii) \(\frac { 1 }{ sinA+cosA+1 } +\frac { 1 }{ sinA+cosA-1 } =secA+cosecA\)
Solution:
(i) sec4 A (1 – sin4 A) – 2 tan2 A = 1
L.H.S = sec4 A (1 – sin4 A) – 2 tan2 A
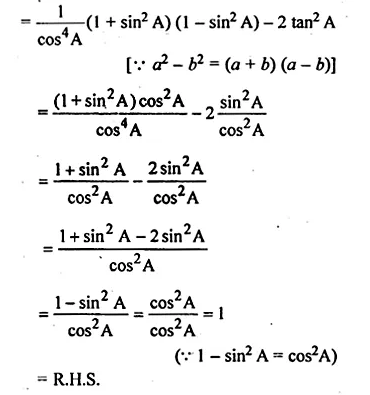
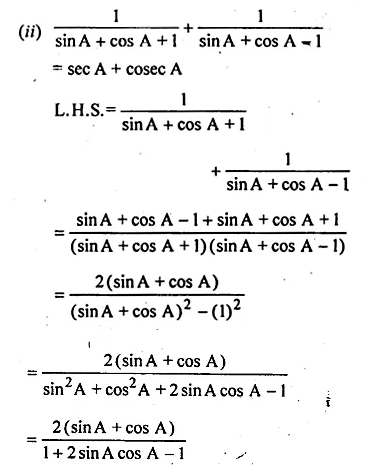
Question 8.
(i) \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta =1\)
(ii) (sec A – tan A)2 (1 + sin A) = 1 – sin A.
Solution:
(i) \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta =1\)
L.H.S = \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta\)
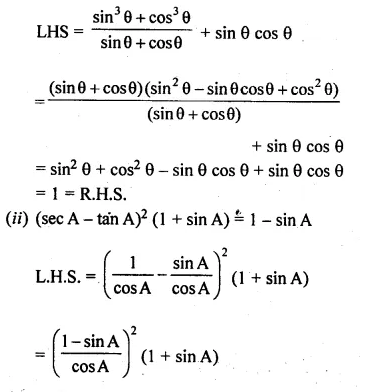
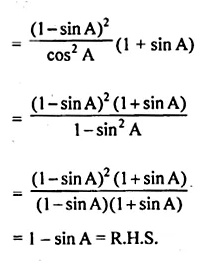
Question 9.
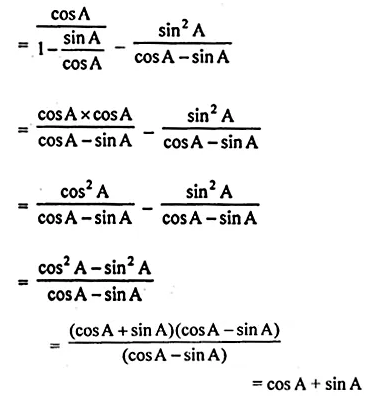
(i) \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } =sinA+cosA \)
(ii) (sec A – cosec A) (1 + tan A + cot A) = tan A sec A – cot A cosec A
(iii) \(\frac { { tan }^{ 2 }\theta }{ { tan }^{ 2 }\theta -1 } -\frac { { cosec }^{ 2 }\theta }{ { sec }^{ 2 }\theta -{ cosec }^{ 2 }\theta } =\frac { 1 }{ { sin }^{ 2 }\theta -{ cos }^{ 2 }\theta } \)
Solution:
(i) \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } =sinA+cosA \)
L.H.S = \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } \)
![]()
Question 10.
\(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } =\frac { 2 }{ { sin }^{ 2 }A-{ cos }^{ 2 }A } =\frac { 2 }{ 1-2{ cos }^{ 2 }A } =\frac { { 2sec }^{ 2 }A }{ { tan }^{ 2 }A-1 } \)
Solution:
\(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } =\frac { 2 }{ { sin }^{ 2 }A-{ cos }^{ 2 }A } =\frac { 2 }{ 1-2{ cos }^{ 2 }A } =\frac { { 2sec }^{ 2 }A }{ { tan }^{ 2 }A-1 } \)
L.H.S = \(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } \)
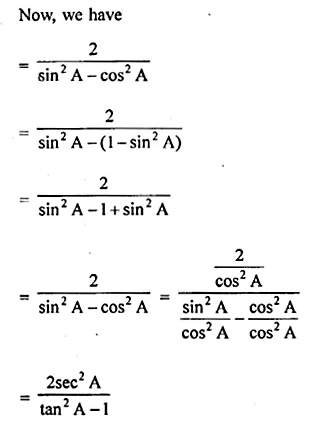
Question 11.
2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1 = θ
Solution:
2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1 = θ
L.H.S = 2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1
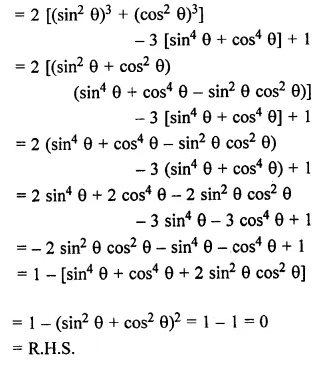
Question 12.
If cot θ + cos θ = m, cot θ – cos θ = n, then prove that (m2 – n2)2 = 16 run.
Solution:
cot θ + cos θ = m…..(i)
cot θ – cos θ = n……(ii)
Adding (i)&(ii) we get

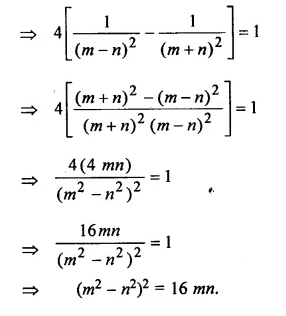
Question 13.
If sec θ + tan θ = p, prove that sin θ = \(\frac { { p }^{ 2 }-1 }{ { p }^{ 2 }+1 } \)
Solution:
sec θ + tan θ = p,
prove that sin θ = \(\frac { { p }^{ 2 }-1 }{ { p }^{ 2 }+1 } \)
\(\frac { 1 }{ cos\theta } +\frac { sin\theta }{ cos\theta } =p\)
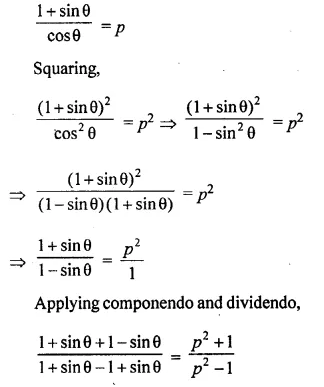
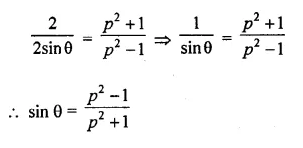
Question 14.
If tan A = n tan B and sin A = m sin B, prove that cos2 A = \(\frac { { m }^{ 2 }-1 }{ { n }^{ 2 }-1 } \)
Solution:
m = \(\\ \frac { sinA }{ sinB } \)
n = \(\\ \frac { tanA }{ tanB } \)
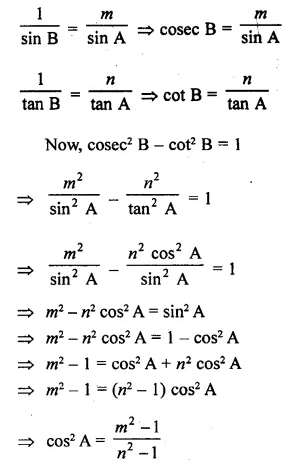
Question 15.
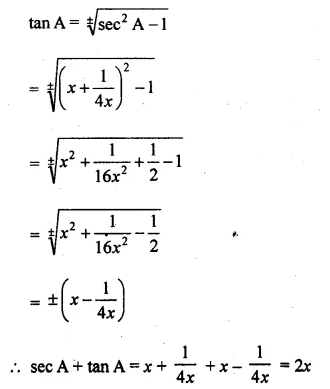
If sec A = \(x+ \frac { 1 }{ 4x } \), then prove that sec A + tan A = 2x or \(\\ \frac { 1 }{ 2x } \)
Solution:
sec A = \(x+ \frac { 1 }{ 4x } \)
To prove that sec A + tan A = 2x or \(\\ \frac { 1 }{ 2x } \)
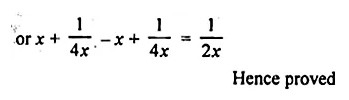
Question 16.
When 0° < θ < 90°, solve the following equations:
(i) 2 cos2 θ + sin θ – 2 = 0
(ii) 3 cos θ = 2 sin2 θ
(iii) sec2 θ – 2 tan θ = 0
(iv) tan2 θ = 3 (sec θ – 1).
Solution:
0° < θ < 90°
(i) 2 cos2 θ + sin θ – 2 = 0
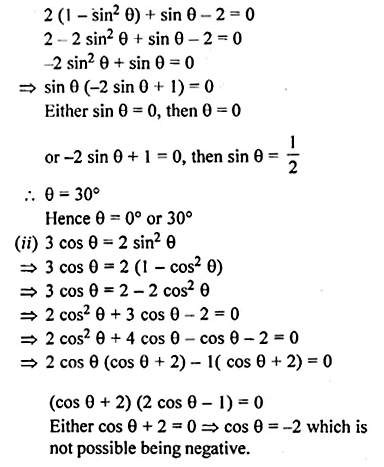
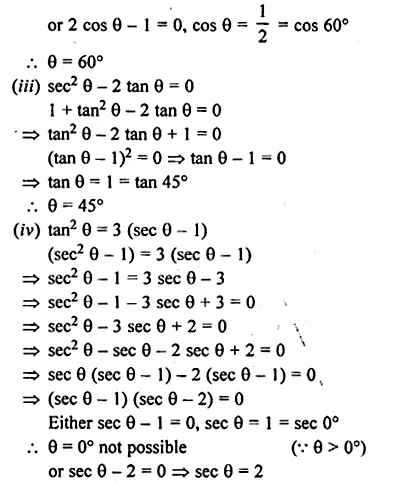
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Identities Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Identities Chapter Test, drop a comment below and we will get back to you at the earliest.