Unit Circle and Trig Graphs
The “Unit Circle” is a circle with a radius of 1.
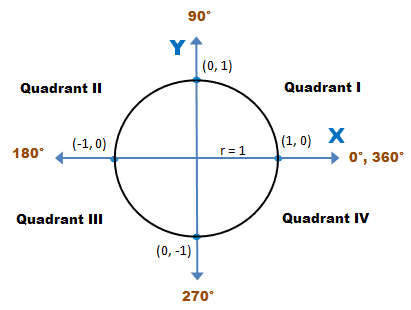
A unit circle is the source for the generation of the trigonometric function graphs.
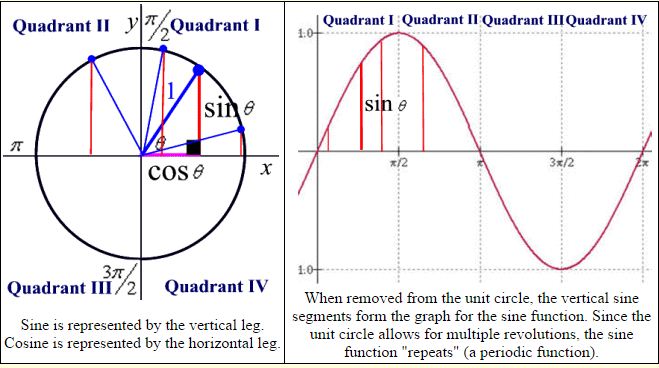
The quadrants from the unit circle, when placed horizontally in numerical order, create the basis for the trigonometric graphs. This process of creating graphs from the unit circle is often called “unwrapping” the unit circle.
Generate the Sine Function:
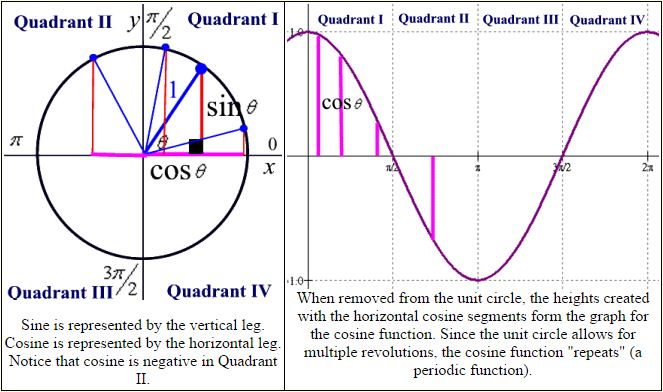
Generate the Cosine Function:
All of the trigonometric functions:
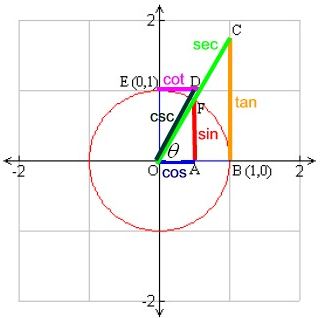
Each of the six trig functions can be thought of as a length related to the unit circle, in a manner similar to that seen above.
We have seen that the sine (AF) and cosine (OA) functions are distances from a point on the unit circle to the axes.
The tangent (BC) and cotangent (ED) functions are the lengths of the line segments tangent to the unit circle from the axis to the terminal ray of angle .
The secant (OC) and cosecant (OD) functions are the lengths on the rays (or secant lines), from the origin to its intersection with the tangent lines.