What are the Trapezoidal rule and Simpson’s rule in Numerical Integration?
Numerical integration
It is the process of computing the value of a definite integral when we are given a set of numerical values of the integrand f(x) corresponding to some values of the independent variable x. Trapezoidal Rule Calculator simply requires input function, range and number of trapezoids in the specified input fields to get the exact results within no time.
If \(I=\int _{ a }^{ b }{ ydx }\). Then I represents the area of the region R under the curve y = f(x) between the ordinates x = a, x = b and the x–axis.
Trapezoidal rule
Let y = f(x) be a function defined on [a, b] which is divided into n equal sub-intervals each of width h so that b – a = nh.
Let the values of f(x) for (n+1) equidistant arguments x0 = a, x1 = x0 + h, x2 = x0 + 2h,……, xn = x0 + nh = b be y0, y1, y2, ….. yn respectively.
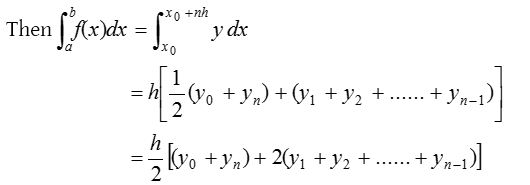
This rule is known as Trapezoidal rule .
The geometrical significance of this rule is that the curve y = f(x) is replaced by n straight lines joining the points (x0, y0) and (x1, y1); (x1, y1) and (x2, y2);…….; (xn−1, yn−1) and (xn, yn). The area bounded by the curve y = f(x). The ordinate x = x0 and x = xn and the x-axis, is then approximately equivalent to the sum of the areas of the n trapeziums obtained.
Simpson’s one third rule
Let y = f(x) be a function defined on [a, b] which is divided into n (an even number) equal parts each of width h, so that b – a = nh.
Suppose the function y = f(x) attains values y0, y1, y2, ….. yn at n+1 equidistant points x0 = a, x1 = x0 + h, x2 = x0 + 2h,……, xn = x0 + nh = b respectively. Then
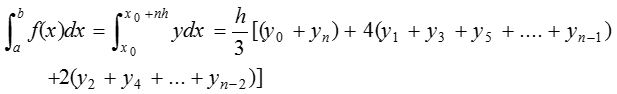
= (one-third of the distance between two consecutive ordinates) [(sum of the extreme ordinates) + 4(sum of odd ordinates) + 2(sum of even ordinates)]
This formula is known as Simpson’s one-third rule. Its geometric significance is that we replace the graph of the given function by n/2 arcs of second degree polynomials, or parabolas with vertical axes. It is to note here that the interval [a, b] is divided into an even number of subinterval of equal width.
Simpson’s rule yield more accurate results than the trapezoidal rule. Small size of interval gives more accuracy.