Formulas for Angles in Circles Formed by Radii, Chords, Tangents, Secants
Formulas for Working with Angles in Circles
(Intercepted arcs are arcs “cut off” or “lying between” the sides of the specified angles.)
There are basically five circle formulas that you need to remember:
1. Central Angle:
A central angle is an angle formed by two intersecting radii such that its vertex is at the center of the circle.
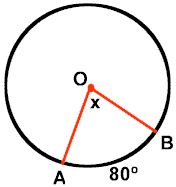
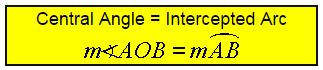 ∠AOB is a central angle.
∠AOB is a central angle.
Its intercepted arc is the minor arc from A to B.
m∠AOB = 80°
Theorem involving central angles:
In a circle, or congruent circles, congruent central angles have congruent arcs.
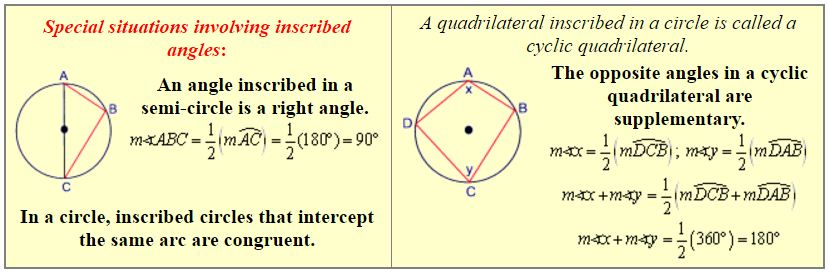
2. Inscribed Angle:
An inscribed angle is an angle with its vertex “on” the circle, formed by two intersecting chords.
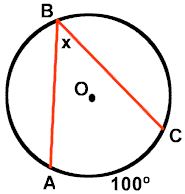
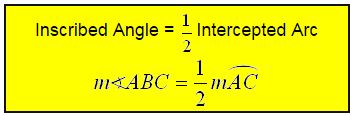 ∠ABC is an inscribed angle.
∠ABC is an inscribed angle.
Its intercepted arc is the minor arc from A to C.
m∠ABC = 50°
3. Tangent Chord Angle:
An angle formed by an intersecting tangent and chord has its vertex “on” the circle.
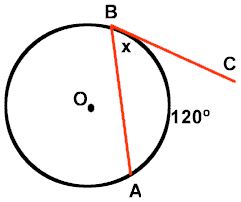
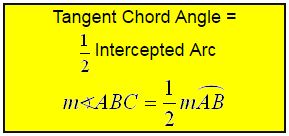 ∠ABC is an angle formed by a tangent and chord.
∠ABC is an angle formed by a tangent and chord.
Its intercepted arc is the minor arc from A to B.
m∠ABC = 60°
4. Angle Formed Inside of a Circle by Two Intersecting Chords:
When two chords intersect “inside” a circle, four angles are formed. At the point of intersection, two sets of vertical angles can be seen in the corners of the X that is formed on the picture. Remember: vertical angles are equal.
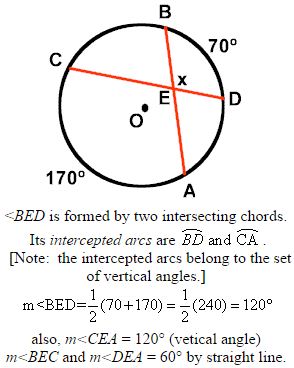
 Once you have found ONE of these angles, you automatically know the sizes of the other three by using your knowledge of vertical angles (being congruent) and adjacent angles forming a straight line (measures adding to 180).
Once you have found ONE of these angles, you automatically know the sizes of the other three by using your knowledge of vertical angles (being congruent) and adjacent angles forming a straight line (measures adding to 180).
5. Angle Formed Outside of a Circle by the Intersection of:
“Two Tangents” or “Two Secants” or “a Tangent and a Secant”.
The formulas for all THREE of these situations are the same: Angle Formed Outside = \(\frac { 1 }{ 2 } \) Difference of Intercepted Arcs (When subtracting, start with the larger arc.)
 Special situation for this set up: It can be proven that ∠ABC and central ∠AOC are supplementary. Thus the angle formed by the two tangents and its first intercepted arc also add to 180º.
Special situation for this set up: It can be proven that ∠ABC and central ∠AOC are supplementary. Thus the angle formed by the two tangents and its first intercepted arc also add to 180º.
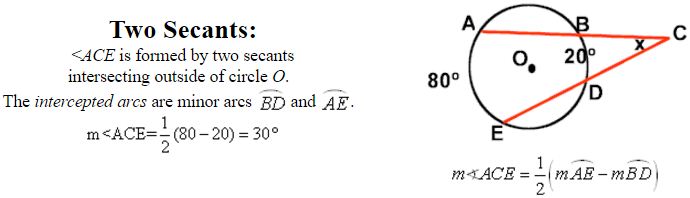

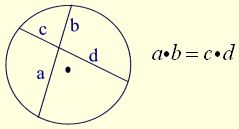 Intersecting Chords Rule:
Intersecting Chords Rule:
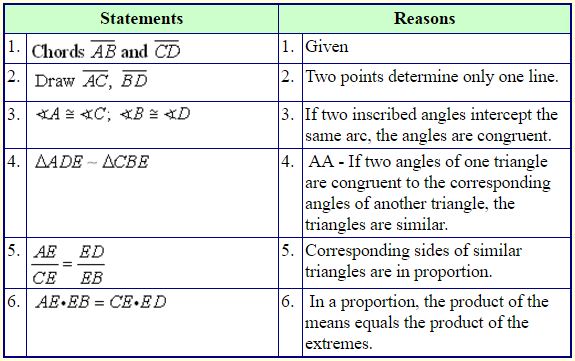 Theorem 2:
Theorem 2: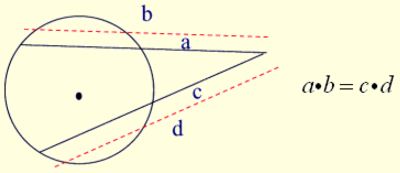 Secant-Secant Rule:
Secant-Secant Rule: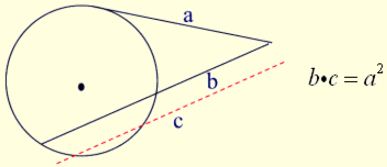 Secant-Tangent Rule:
Secant-Tangent Rule: