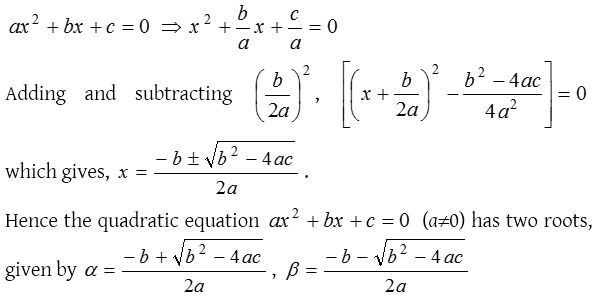Quadratic Equations

Nature Of The Roots Of A Quadratic Equation

by

Nature Of The Roots Of A Quadratic Equation

The nature of the roots depends on the value of b2 – 4ac. bx2 – 4ac is called the discriminant of the quadratic equation ax2 + bx + c = 0 and is generally, denoted by D.
∴ D = b2 – 4ac
If D > 0, i..e., b2 – 4ac > 0, i.e., b2 – 4ac is positive; the roots are real and unequal. Also,
(i) If b2 – 4ac is a perfect square, the roots are rational and unequal.
(ii) If b2 – 4ac is positive but not perfect square, the roots are irrational and unequal.
If D = 0, i.e., b2 – 4ac = 0; the roots are real and equal.
If D < 0, i.e., b2 – 4ac < 0; i.e., b2 – 4ac is negative; the roots are not real, i.e., the roots are imaginary.

Nature Of The Roots Of A Quadratic Equation With Examples

Example 1:    Without solving, examine the nature of roots of the equation 2x2 + 2x + 3 = 0.
Sol.     Comparing 2x2 + 2x + 3 = 0 with ax2 + bx + c = 0
we get: a = 2, b = 2 and c = 3
D = b2 – 4ac = (2)2 – 4 × 2 × 3 = 4 – 24
= – 20; which is negative.
∴ The roots of the given equation are imaginary.

Example 2:    Without solving, examine the nature of roots of the equation 2x2 – 7x + 3 = 0.
Sol.     Comparing 2x2 – 7x + 3 = 0 with ax2 + bx + c = 0;
we get: a = 2, b = – 7 and c = 3
D = b2 – 4ac = (–7)2 – 4 × 2 × 3
= 49 – 24 = 25, which is perfect square.
∴ The roots of the given equation are rational and unequal.

Example 3:    Without solving, examine the nature of roots of the equation x2 – 5x – 2 = 0.
Sol.     Comparing x2 – 5x – 2 = 0 with ax2 + bx + c = 0;
we get: a = 1, b = – 5 and c = – 2
D = b2 – 4ac = (–5)2 – 4 × 1 × – 2
= 25 + 8 = 33 ; which is positive but not a perfect square.
∴ The roots of the given equation are irrational and unequal.

Example 4:    Without solving, examine the nature of roots of the equation 4x2 – 4x + 1 = 0.
Sol.     Comparing 4x2 – 4x + 1 = 0 with ax2 + bx + c = 0;
we get: a = 4, b = – 4, and c = 1
D = b2 – 4ac = (–4)2 – 4 × 4 × 1
= 16 – 16 = 0
∴ Roots are real and equal.

Example 5:    For what value of m, are the roots of the equation (3m + 1)x2 + (11 + m) x + 9 = 0 equal?
Sol.    Comparing the given equation with ax2 + bx + c = 0;
we get : a = 3m + 1, b = 11 + m and c = 9
∴ Discriminant, D = b2 – 4ac
= (11 + m)2 – 4(3m + 1) × 9
= 121 + 22m + m2 – 108m – 36
= m2 – 86m + 85
= m2 – 85m – m + 85
= m(m – 85) – 1 (m – 85)
= (m – 85) (m – 1)
Since the roots are equal, D = 0
⇒ (m – 85) (m – 1) = 0
⇒ m – 85 = 0 or m – 1 = 0
⇒ m = 85 or m = 1

Solving A Quadratic Equation By Factoring

by

Solving A Quadratic Equation By Factoring

Since, 3x2 – 5x + 2 is a quadratic polynomial;
3x2 – 5x + 2 = 0 is a quadratic equation.
Also,
3x2 – 5x + 2 = 3x2 – 3x – 2x + 2 [Factorising]
= 3x (x – 1) – 2(x – 1)
= (x – 1) (3x – 2)
In the same way :
3x2 – 5x + 2 = 0   ⇒   3x2 – 3x – 2x + 2 = 0   [Factorising L.H.S.]
⇒   (x – 1) (3x – 2) = 0
i.e.,  x – 1 = 0   or   3x – 2 = 0
⇒  x = 1   or   x = 2/3
which is the solution of given quadratic equation.
In order to solve the given Quadratic Equation:
1. Clear the fractions and brackets, if given.
2. By transfering each term to the left hand side; express the given equation as
ax2 + bx + c = 0   or   a + bx + cx2 = 0
3. Factorise left hand side of the equation obtained (the right hand side being zero).
4. By putting each factor equal to zero; solve it.

Solving A Quadratic Equation By Factoring With Examples

Example 1:    Solve  (i) x2 + 3x – 18 = 0       (ii) (x – 4) (5x + 2) = 0
(iii) 2x2 + ax – a2 = 0;   where ‘a’ is a real number.
Sol.    (i) x2 + 3x – 18 = 0
⇒ x2 + 6x – 3x – 18 = 0
⇒ x(x + 6) – 3(x + 6) = 0
i.e., (x + 6) (x – 3) = 0
⇒ x + 6 = 0 or x – 3 = 0
⇒ x = – 6 or x = 3
Roots of the given equation are – 6 and 3
(ii) (x – 4) (5x + 2) = 0
⇒ x – 4 = 0 or 5x + 2 = 0
x = 4 or x = – 2/5
(iii) 2x2 + ax – a2 = 0
⇒ 2x2 + 2ax – ax – a2 = 0
⇒ 2x(x + a) – a(x + a) = 0
i.e., (x + a) (2x – a) = 0
⇒ x + a = 0 or 2x – a = 0
⇒ x = – a or  x = a/2

Example 2:    Solve the following quadratic equations
(i) x2 + 5x = 0         (ii) x2 = 3x          (iii) x2 = 4
Sol.    (i) x2 + 5x = 0  ⇒  x(x + 5) = 0
⇒  x = 0 or x + 5 = 0
⇒  x = 0 or x = – 5
(ii) x2 = 3x
⇒ x2 – 3x = 0
⇒  x(x – 3) = 0
⇒  x = 0 or x = 3
(iii) x2 = 4
⇒  x = ± 2

Example 3:     Solve the following quadratic equations
(i) 7x2 = 8 – 10x            (ii) 3(x2 – 4) = 5x              (iii) x(x + 1) + (x + 2) (x + 3) = 42
Sol.    (i) 7x2 = 8 – 10x
⇒ 7x2 + 10x – 8 = 0
⇒ 7x2 + 14x – 4x – 8 = 0
⇒ 7x(x + 2) – 4(x + 2) = 0
⇒ (x + 2) (7x – 4) = 0
⇒ x + 2 = 0   or   7x – 4 = 0
⇒ x = – 2   or   x = 4/7
(ii) 3(x2 – 4) = 5x
⇒ 3x2 – 5x – 12 = 0
⇒ 3x2 – 9x + 4x –¬ 12 = 0
⇒ 3x(x – 3) + 4(x – 3) = 0
⇒ (x – 3) (3x + 4) = 0
⇒ x – 3 = 0   or   3x + 4 = 0
⇒ x = 3   or   x = –4/3
(iii) x(x + 1) + (x + 2) (x + 3) = 42
⇒ x2 + x + x2 + 3x + 2x + 6 – 42 = 0
⇒ 2x2 + 6x – 36 = 0
⇒ x2 + 3x – 18 = 0
⇒ x2 + 6x – 3x – 18 = 0
⇒ x(x + 6) – 3(x + 6) = 0
⇒ (x + 6) (x – 3) = 0
⇒ x = – 6   or   x = 3

Example 4:     Solve for x : 12abx2 – (9a2 – 8b2) x – 6ab = 0
Given equation is 12abx2 – (9a2 – 8b2) x – 6ab = 0
⇒ 3ax(4bx – 3a) + 2b(4bx – 3a) = 0
⇒ (4bx – 3a) (3ax + 2b) = 0
⇒ 4bx – 3a = 0   or   3ax + 2b = 0
⇒ x =3a/4b   or   x = – 2b/3a

Solving Factorable Quadratic Equations

by

Solving Factorable Quadratic Equations

A quadratic equation is a polynomial equation of degree two. The standard form is ax² + bx + c = 0.

There’s no magic to solving quadratic equations. Quadratic equations can be solved by factoring and also by graphing.

The factoring method of solution:

Let’s do a quick review of factoring.

Factoring Method:

  1. Express the equation in the form ax2 + bx + c = 0.
  2. Factor the left hand side (if 0 is on the right).
  3. Set each of the two factors equal to zero.
  4. Solve for x to determine the roots (or zeros).

Simple quadratic equations with rational roots can be solved by factoring.
If you can factor, you will be able to solve factorable quadratic equations.

Examples of Solving Quadratic Equations by Factoring:

Example 1: 
Factoring with GCF
(greatest common factor):
Find the largest value which can be factored from each term on the left side of the quadratic equation.
The roots (zeros) correspond to the locations of the x-intercepts of the function y = 4x2 – 28x.
Solving Factorable Quadratic Equations 1a

Example 2:
Factoring Trinomial with Leading Coefficient of One:
When the leading coefficient is one, the product of the roots will be the constant term, and the sum of the roots will be the coefficient of the middle x-term.

Solving Factorable Quadratic Equations 2a

Example 3:
Factoring Difference of Two Squares:
Remember the pattern for the difference of two squares, where the factors are identical except for the sign between the terms.
Solving Factorable Quadratic Equations 3a

Example 4:
Factoring Trinomial with Leading Coefficient Not One:
Life gets more difficult when the leading coefficient is not one.
Solving Factorable Quadratic Equations 4a

Example 5:
Where’s the x2 ?
Sometimes you have to “work” on the equation to get the needed quadratic form. In this case, distribute, and the x2 will appear.
Solving Factorable Quadratic Equations 5a

Example 6:
Dealing with Proportions:
x2 may appear when cross multiplying (“product of the means equals product of the extremes”) is employed in a proportion.
Solving Factorable Quadratic Equations 6a

Quadratic Equations

by

Quadratic Equations

An equation in which the highest power of the unknown quantity is two is called quadratic equation.
Quadratic Equations 1

Types of quadratic equation

Quadratic equations are of two types:

Purely quadraticAdfected quadratic
ax2 + c = 0 where a, c ∈ C and b = 0, a ≠ 0ax2 + bx + c = 0 where a, b, c ∈ C and a ≠ 0, b ≠ 0

Roots of a quadratic equation:
The values of variable x which satisfy the quadratic equation is called roots of quadratic equation.

Solution of quadratic equation

(1) Factorization method
Let ax2 + bx + c = a(x – α)(x – β) = 0.
Then x = α and x = β will satisfy the given equation.
Hence, factorize the equation and equating each factor to zero gives roots of the equation.
Example: 3x2 – 2x + 1 = 0 ⇒(x – 1)(3x + 1) = 0; x = 1, -1/3

(2) Sri Dharacharya method 
By completing the perfect square as
Quadratic Equations 2
Every quadratic equation has two and only two roots.

https://www.youtube.com/watch?v=Nf1Fs8ln8tw

Nature of roots

In a quadratic equation ax2 + bx + c = 0, let us suppose that are real and a ≠ 0. The following is true about the nature of its roots.

  1. The equation has real and distinct roots if and only if D ≡ b2 – 4ac > 0.
  2. The equation has real and coincident (equal) roots if and only if D ≡ b2 – 4ac = 0.
  3. The equation has complex roots of the form α ± iβ, α ≠ 0 if and only if D ≡ b2 – 4ac < 0.
  4. The equation has rational roots if and only if a, b, c ∈ Q (the set of rational numbers) and D ≡ b2 – 4ac is a perfect square (of a rational number).
  5. The equation has (unequal) irrational (surd form) roots if and only if D ≡ b2 – 4ac > 0 and not a perfect square even if a, b and c are rational. In this case if p + √q, p,q rational is an irrational root, then p – √q is also a root (a, b, c being rational).
  6. α + iβ (β ≠ 0 and α, β ∈ R) is a root if and only if its conjugate α – iβ is a root, that is complex roots occur in pairs in a quadratic equation. In case the equation is satisfied by more than two complex numbers, then it reduces to an identity.
    0.x2 + 0.x + 0 = 0, i.e., a = 0 = b = c.

Relations between roots and coefficients

(1) Relation between roots and coefficients of quadratic equation: If α and β are the roots of quadratic equation , (a ≠ 0) then
Quadratic Equations 3
(2) Formation of an equation with given roots: A quadratic equation whose roots are α and β is given by (x – α)(x – β) = 0.
∴ x2 – (α+iβ)x + αβ = 0
i.e. x2 – (sum of roots)x + (product of roots) = 0
∴ x2 – Sx + P = 0
(3) Symmetric function of the roots : A function of α and β is said to be a symmetric function, if it remains unchanged when α and β are interchanged.
For example, α2 + β2 + 2αβ is a symmetric function of α and β whereas α2 + β2 + 2αβ is not a symmetric function of α and β.
In order to find the value of a symmetric function of α and β, express the given function in terms of α + β and αβ. The following results may be useful.
Quadratic Equations 4

Properties of quadratic equation

  1. If f(a) and f(b) are of opposite signs then at least one or in general odd number of roots of the equation lie between a and b.
  2. If then f(a) = f(b) there exists a point c between a and b such that f(c) = 0, a<c<b.
  3. If α is a root of the equation f(x) = 0 then the polynomial f(x) is exactly divisible by (x – α), then (x – α) is factor of f(x).
  4. If the roots of the quadratic equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0 are in the same ratio [i.e. α1/β1 = α2/β2] then b12/b22 = a1c1/a2c2.

Solving A Quadratic Equation By Completing The Square

by

Solving A Quadratic Equation By Completing The Square

Every quadratic equation can be converted in the form:
(x + a)2 – b2 = 0 or (x – a)2 – b2 = 0.
Steps:
1. Bring, if required, all the term of the quadratic equation to the left hand side.
2. Express the terms containing x as x2 + 2xy   or   x2 – 2xy.
3. Add and subtract y2 to get x2 + 2xy + y2 – y2   or   x2 – 2xy + y2 – y2; which gives
(x + y)2 – y2 or (x – y)2 – y2.
Thus,
(i) x2 + 8x = 0 ⇒  x2 + 2x × 4 = 0
⇒ x2 + 2x × 4 + 42 – 42 = 0
⇒ (x + 4)2 – 16 = 0
(ii) x2 – 8x = 0 ⇒ x2 – 2 × x × 4 = 0
⇒ x2 – 2 × x × 4 + 42 – 42 = 0
⇒ (x – 4)2 – 16 = 0

Solving A Quadratic Equation By Completing The Square 1

Solving A Quadratic Equation By Completing The Square With Examples

Example 1:    Find the roots of the quadratic equation 2x2 – 7x + 3 = 0
(if they exist) by the method of completing the square.
Sol.     2x2 – 7x + 3 = 0
\(\Rightarrow {{x}^{2}}-\frac{7}{2}x+\frac{3}{2}=0 \)    [Dividing each term by 2]
\(\Rightarrow {{x}^{2}}-2\times x\times \frac{7}{4}+\frac{3}{2}=0 \)
\(\Rightarrow {{x}^{2}}-2\times x\times \frac{7}{4}+{{\left( \frac{7}{4} \right)}^{2}}-{{\left( \frac{7}{4} \right)}^{2}}+\frac{3}{2}=0 \)
\(\Rightarrow {{\left( x-\frac{7}{4} \right)}^{2}}-\frac{49}{16}+\frac{3}{2}=0 \)
\(\Rightarrow {{\left( x-\frac{7}{4} \right)}^{2}}-\left( \frac{49-24}{16} \right)=0 \)
\(\Rightarrow {{\left( x-\frac{7}{4} \right)}^{2}}-\frac{25}{16}=0 \)
\(i.e.,{{\left( x-\frac{7}{4} \right)}^{2}}=\frac{25}{16}\Rightarrow x-\frac{7}{4}=\pm \frac{5}{4} \)
\(i.e.,x-\frac{7}{4}=\frac{5}{4}\text{   or    }x-\frac{7}{4}=-\frac{5}{4}\text{  } \)
\(\Rightarrow x=\frac{7}{4}+\frac{5}{4}\text{   or    }x=\frac{7}{4}-\frac{5}{4}\text{  } \)
\(\Rightarrow x=3\text{  or    }x=\frac{1}{2} \)

Example 2:    Find the roots of the quadratic equation 4x2 + 4√3x + 3 = 0
Sol.    4x2 + 4√3x + 3 = 0
\( \Rightarrow {{x}^{2}}+\sqrt{3}x+\frac{3}{4}=0 \)
\(i.e.,\text{ }{{x}^{2}}+2\times x\times \frac{\sqrt{3}}{2}+{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}-{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}+\frac{3}{4}=0 \)
\(\Rightarrow {{\left( x+\frac{\sqrt{3}}{2} \right)}^{2}}-\frac{3}{4}+\frac{3}{4}=0 \)
\(i.e.,{{\left( x+\frac{\sqrt{3}}{2} \right)}^{2}}=0 \)
\(\Rightarrow x+\frac{\sqrt{3}}{2}=0\text{    and    }x=\frac{-\sqrt{3}}{2} \)

Example 3:    Find the roots of the quadratic equation 2x2 + x + 4 = 0
Sol.    2x2 + x + 4 = 0
\(\Rightarrow {{x}^{2}}+\frac{x}{2}+2=0 \)
\(i.e.,~{{x}^{2}}+2\times x\times \frac{1}{4}+{{\left( \frac{1}{4} \right)}^{2}}-{{\left( \frac{1}{4} \right)}^{2}}+2=0 \)
\(\Rightarrow {{\left( x+\frac{1}{4} \right)}^{2}}-\frac{1}{16}+2=0 \)
\(\Rightarrow {{\left( x+\frac{1}{4} \right)}^{2}}+\frac{31}{16}=0 \)
\(i.e.,{{\left( x+\frac{1}{4} \right)}^{2}}=-\frac{31}{16} \)
This is not possible as the square of a real number can not be negative.

Foe More Solved Examples