Selina Concise Mathematics Class 10 ICSE Solutions Probability
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 10 Mathematics Chapter 25 Probability. You can download the Selina Concise Mathematics ICSE Solutions for Class 10 with Free PDF download option. Selina Publishers Concise Mathematics for Class 10 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability
Probability Exercise 25(A) – Selina Concise Mathematics Class 10 ICSE Solutions
Question 1.
A coin is tossed once. Find the probability of:
(i) getting a tail
(ii) not getting a tail
Solution:

Question 2.
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is:
(i) a black ball.
(ii) a red ball.
(iii) a white ball.
(iv) not a red ball.
(v) not a black ball.
Solution:

Question 3.
In a single throw of a die, find the probability of getting a number:
(i) greater than 4.
(ii) less than or equal to 4.
(iii) not greater than 4.
Solution:
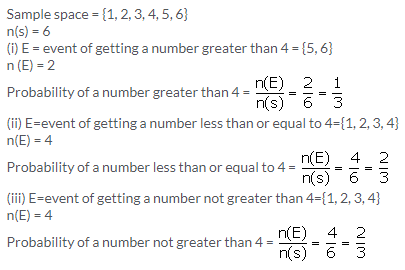
Question 4.
In a single throw of a die, find the probability that the number:
(i) will be an even number.
(ii) will not be an even number.
(iii) will be an odd number.
Solution:

Question 5.
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will:
(i) be a black card.
(ii) not be a red card.
(iii) be a red card.
(iv) be a face card.
(v) be a face card of red colour.
Solution:
Total number of cards = 52
Total number of outcomes = P(s) = 52
There are 13 cards of each type. The cards of heart and diamond are red in colour. Spade and diamond are black. So, there are 26 red cards and 26 black cards.
(i) Number of black cards in a deck = 26
P(E) = favourable outcomes for the event of drawing a black card = 26

(iv) There are 52 cards in a deck of cards, and 12 of these cards are face cards (4 kings, 4 queens, and 4 jacks).
P(E) = 12

Question 6.
(i) If A and B are two complementary events then what is the relation between P(A) and P(B)?
(ii) If the probability of happening an event A is 0.46. What will be the probability of not happening of the event A?
Solution:
(i) Two complementary events, taken together, include all the outcomes for an experiment and the sum of the probabilities of all outcomes is 1.
P(A) + P(B) = 1
(ii) P(A) = 0.46
Let P(B) be the probability of not happening of event A
We know,
P(A) + P(B) = 1
P(B) = 1 – P(A)
P(B) = 1 – 0.46
P(B) = 0.54
Hence the probability of not happening of event A is 0.54
Question 7.
In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of:
(i) winning of Geeta
(ii) not winning of Ritu
Solution:
(i) Winning of Geeta is a complementary event to winning of Ritu
Therefore,
P(winning of Ritu) + P(winning of Geeta) = 1
P(winning of Geeta) = 1 – P(winning of Ritu)
P(winning of Geeta) = 1 – 0.73
P(winning of Geeta) = 0.27
(ii) Not winning of Ritu is a complementary event to winning of Ritu
Therefore,
P(winning of Ritu) + P(not winning of Ritu) = 1
P(not winning of Ritu) = 1 – P(winning of Ritu)
P(not winning of Ritu) = 1 – 0.73
P(not winning of Ritu) = 0.27
Question 8.
In a race between Mahesh and John, the probability that John will lose the race is 0.54. Find the probability of:
(i) winning of Mahesh
(ii) winning of John
Solution:
(i) But if John looses, Mahesh wins
Hence, probability of John losing the race = Probability of Mahesh winning the race since it is a race between these two only
Therefore, P(winning of Mahesh) = 0.54
(ii) P(winning of Mahesh) + P(winning of John) = 1
0.54 + P(winning of John) = 1
P(winning of John) = 1 – 0.54
P(winning of John) = 0.46
Question 9.
(i) Write the probability of a sure event
(ii) Write the probability of an event when impossible
(iii) For an event E, write a relation representing the range of values of P(E)
Solution:

The number of elements in ‘E’ can’t be less than ‘0’ i.e. negative and greater than the number of elements in S.
Question 10.
In a single throw of die, find the probability of getting:
(i) 5
(ii) 8
(iii) a number less than 8
(iv) a prime number
Solution:

(ii) There are only six possible outcomes in a single throw of a die. If we want to find probability of 8 to come up, then in that case number of possible or favourable outcome is 0 (zero)

Question 11.
A die is thrown once. Find the probability of getting:
(i) an even number
(ii) a number between 3 and 8
(iii) an even number or a multiple of 3
Solution:

Question 12.
Which of the following cannot be the probability of an event?
(i) 3/5
(ii) 2.7
(iii) 43%
(iv) -0.6
(v) -3.2
(vi) 0.35
Solution:

Question 13.
A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:
(i) a white ball
(ii) a black ball
Solution:

Question 14.
A single letter is selected at random from the word ‘Probability’. Find the probability that it is a vowel.
Solution:

Question 15.
Solution:

Probability Exercise 25(B) – Selina Concise Mathematics Class 10 ICSE Solutions
Question 1.
Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be:
(i) an even number
(ii) a multiple of 3
(iii) an even number and a multiple of 3
(iv) an even number or a multiple of 3
Solution:

(iv) From numbers 2 to 10, there are 7 numbers which are even numbers or a multiple of 3 i.e. 2, 3, 4, 6, 8, 9, 10
Favorable number of events = n(E) = 7
![]()
Question 2.
Hundred identical cards are numbered from 1 to 100. The cards The cards are well shuffled and then a card is drawn. Find the probability that the number on card drawn is:
(i) a multiple of 5
(ii) a multiple of 6
(iii) between 40 and 60
(iv) greater than 85
(v) less than 48
Solution:

Question 3.
From 25 identical cards, numbered 1, 2, 3, 4, 5, ……, 24, 25: one card is drawn at random. Find the probability that the number on the card drawn is a multiple of:
(i) 3
(ii) 5
(iii) 3 and 5
(iv) 3 or 5
Solution:

Question 4.
A die is thrown once. Find the probability of getting a number:
(i) less than 3
(ii) greater than or equal to 4
(iii) less than 8
(iv) greater than 6
Solution:

Question 5.
A book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8?
Solution:

Question 6.
A pair of dice is thrown. Find the probability of getting a sum of 10 or more, if 5 appears on the first die.
Solution:

Question 7.
If two coins are tossed once, what is the probability of getting:
(i) both heads.
(ii) at least one head.
(iii) both heads or both tails.
Solution:

Question 8.
Two dice are rolled together. Find the probability of getting:
(i) a total of at least 10.
(ii) a multiple of 2 on one die and an odd number on the other die.
Solution:

Question 9.
A card is drawn from a well shuffled pack of 52 cards. Find the probability that the card drawn is:
(i) a spade(v) Jack or queen
(ii) a red card(vi) ace and king
(iii) a face card(vii) a red and a king
(iv) 5 of heart or diamond(viii) a red or a king
Solution:


Question 10.
A bag contains 16 colored balls. Six are green, 7 are red and 3 are white. A ball is chosen, without looking into the bag. Find the probability that the ball chosen is:
(i) red(v) green or red
(ii) not red(vi) white or green
(iii) white(vii) green or red or white
(iv) not white
Solution:

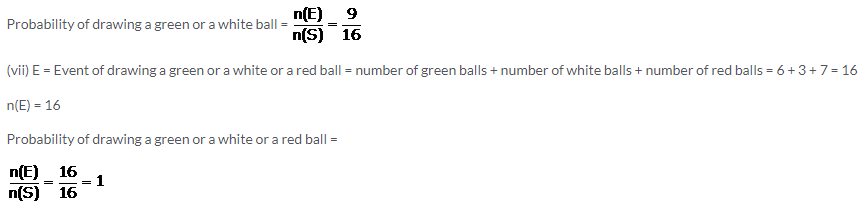
Question 11.
A ball is drawn at random from a box containing 12 white, 16 red and 20 green balls. Determine the probability that the ball drawn is:
(i) white(iii) not green
(ii) red(iv) red or white
Solution:

Question 12.
A card is drawn from a pack of 52 cards. Find the probability that the card drawn is:
(i) a red card
(ii) a black card
(iii) a spade
(iv) an ace
(v) a black ace
(vi) ace of diamonds
(vii) not a club
(viii) a queen or a jack
Solution:


Question 13.
Thirty identical cards are marked with numbers 1 to 30. If one card is drawn at random, find the probability that it is:
(i) a multiple of 4 or 6
(ii) a multiple of 3 and 5
(iii) a multiple of 3 or 5
Solution:

Question 14.
In a single throw of two dice, find the probability of:
(i) a doublet
(ii) a number less than 3 on each dice
(iii) an odd number as a sum
(iv) a total of at most 10
(v) an odd number on one dice and a number less than or equal to 4 on the other dice.
Solution:


Probability Exercise 25(C) – Selina Concise Mathematics Class 10 ICSE Solutions
Question 1.
A bag contains 3 red balls, 4 blue balls and 1 yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it; find the probability that the ball is:
(i) yellow
(ii) red
(iii) not yellow
(iv) neither yellow nor red
Solution:

Question 2.
A dice is thrown once. What is the probability of getting a number:
(i) greater than 2?
(ii) less than or equal to 2?
Solution:
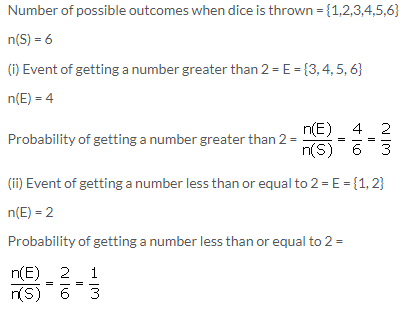
Question 3.
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is:
(i) a face card
(ii) not a face card
(iii) a queen of black card
(iv) a card with number 5 or 6
(v) a card with number less than 8
(vi) a card with number between 2 and 9
Solution:

Question 4.
In a match between A and B:
(i) the probability of winning of A is 0.83. What is the probability of winning of B?
(ii) the probability of losing the match is 0.49 for B. What is the probability of winning of A?
Solution:

Question 5.
A and B are friends. Ignoring the leap year, find the probability that both friends will have:
(i) different birthdays?
(ii) the same birthday?
Solution:

Question 6.
A man tosses two different coins (one of Rs 2 and another of Rs 5) simultaneously. What is the probability that he gets:
(i) at least one head?
(ii) at most one head?
Solution:

Question 7.
A box contains 7 red balls, 8 green balls and 5 white balls. A ball is drawn at random from the box. Find the probability that the ball is:
(i) white
(ii) neither red nor white.
Solution:

Question 8.
All the three face cards of spades are removed from a well shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting:
(i) a black face card
(ii) a queen
(iii) a black card
Solution:

Question 9.
In a musical chairs game, a person has been advised to stop playing the music at any time within 40 seconds after its start. What is the probability that the music will stop within the first 15 seconds?
Solution:

Question 10.
In a bundle of 50 shirts, 44 are good, 4 have minor defects and 2 have major defects. What is the probability that:
(i) it is acceptable to a trader who accepts only a good shirt?
(ii) it is acceptable to a trader who rejects only a shirt with major defects?
Solution:

Question 11.
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is:
(i) 8
(ii) 13
(iii) less than or equal to 12
Solution:

Question 12.
Which of the following cannot be the probability of an event?
(i) 3/7
(ii) 0.82
(iii) 37%
(iv) -2.4
Solution:

Question 13.
If P(E) = 0.59; find P(not E)
Solution:
P(E) + P(not E) = 1
0.59 + P(not E) = 1
P(not E) = 1 – 0.59 = 0.41
Question 14.
A bag contains a certain number of red balls. A ball is drawn. Find the probability that the ball drawn is:
(i) black
(ii) red
Solution:

Question 15.
The probability that two boys do not have the same birthday is 0.897. What is the probability that the two boys have the same birthday?
Solution:
P(do not have the same birthday)+P(have same birthday) = 1
0.897 + P(have same birthday) = 1
P(have same birthday) = 1 – 0.897
P(have same birthday) = 0.103
Question 16.
A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be:
(i) not red?
(ii) neither red nor green?
(iii) white or green?
Solution:

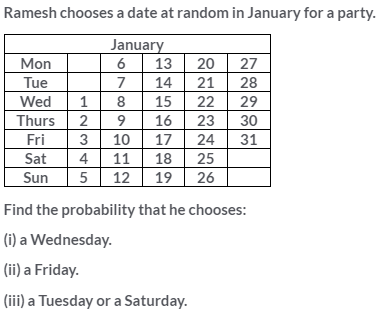
Question 17.
A bag contains twenty Rs 5 coins, fifty Rs 2 coins and thirty Re 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin:
(i) will be a Re 1 coin?
(ii) will not be a Rs 2 coin?
(iii) will neither be a Rs 5 coin nor be a Re 1 coin?
Solution:
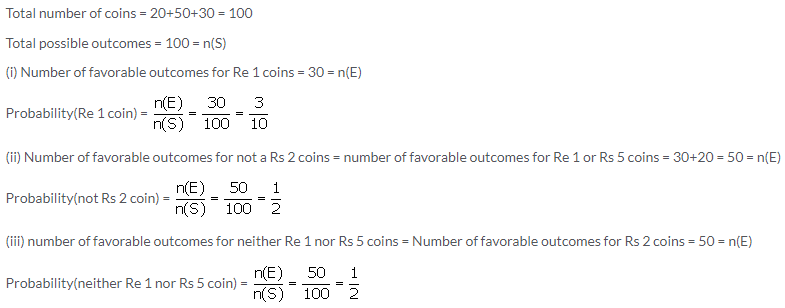
Question 18.
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.
If the outcomes are equally likely, find the probability that the pointer will point at:
(i) 6
(ii) an even number
(iii) a prime number
(iv) a number greater than 8
(v) a number less than or equal to 9
(vi) a number between 3 and 11
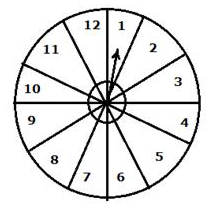
Solution:

Question 19.
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting:
(i) a queen of red color
(ii) a black face card
(iii) the jack or the queen of the hearts
(iv) a diamond
(v) a diamond or a spade
Solution:

Question 20.
From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled. Now one card is drawn from the remaining deck. Find the probability that the card drawn is:
(i) a black card
(ii) 8 of red color
(iii) a king of black color
Solution:

Question 21.
Seven cards:- the eight, the nine, the ten, jack, queen, king and ace of diamonds are well shuffled. One card is then picked up at random.
(i) What is the probability that the card drawn is the eight or the king?
(ii) If the king is drawn and put aside, what is the probability that the second card picked up is:
a) an ace? b) a king?
Solution:

Question 22.
A box contains 150 bulbs out of which 15 are defective. It is not possible to just look at a bulb and tell whether or not it is defective. One bulb is taken out at random from this box. Calculate the probability that the bulb taken out is:
(i) a good one
(ii) a defective one
Solution:

Question 23.
(i) 4 defective pens are accidentally mixed with 16 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is drawn at random from the lot. What is the probability that the pen is defective?
(ii) Suppose the pen drawn in (i) is defective and is not replaced. Now one more pen is drawn at random from the rest. What is the probability that this pen is:
a) defective
b) not defective?
Solution:

Question 24.
A bag contains 100 identical marble stones which are numbered 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears:
(i) a perfect square number
(ii) a number divisible by 4
(iii) a number divisible by 5
(iv) a number divisible by 4 or 5
(v) a number divisible by 4 and 5
Solution:

Question 25.
A circle with diameter 20 cm is drawn somewhere on a rectangular piece of paper with length 40 cm and width 30 cm. This paper is kept horizontal on table top and a die, very small in size, is dropped on the rectangular paper without seeing towards it. If the die falls and lands on paper only, find the probability that it will fall and land:
(i) inside the circle
(ii) outside the circle
Solution:

Question 26.
Two dice (each bearing numbers 1 to 6) are rolled together. Find the probability that the sum of the numbers on the upper-most faces of two dice is:
(i) 4 or 5
(ii) 7, 8 or 9
(iii) between 5 and 8
(iv) more than 10
(v) less than 6
Solution:

Question 27.
Three coins are tossed together. Write all the possible outcomes. Now, find the probability of getting:
(i) exactly two heads
(ii) at least two heads
(iii) at most two heads
(iv) all tails
(v) at least one tail
Solution:

Question 28.
Two dice are thrown simultaneously. What is the probability that:
(i) 4 will not come up either time?
(ii) 4 will come up at least once?
Solution:

Question 29.
Cards marked with numbers 1, 2, 3 ……… 20 are well shuffled and a card is drawn at random. What is the probability that the number on the card is:
(i) a prime number
(ii) divisible by 3
(iii) a perfect square
Solution:

Question 30.
Offices in Delhi are open for five days in a week (Monday to Friday). Two employees of an office remain absent for one day in the same particular week. Find the probability that they remain absent on:
(i) the same day
(ii) consecutive day
(iii) different days
Solution:

Question 31.
A box contains some black balls and 30 white balls. If the probability of drawing a black ball is two-fifths of a white ball; find the number of black balls in the box.
Solution:

Question 32.
From a pack of 52 playing cards, all cards whose numbers are multiples of 3 are removed. A card is now drawn at random. What is the probability that the card drawn is
(i) A face card (King, Jack or Queen)
(ii) An even numbered red card?
Solution:

Question 33.
A die has 6 faces marked by the given numbers as shown below:
![]()
The die is thrown once. What is the probability of getting
(i) a positive integer?
(ii) an integer greater than -3?
(iii) the smallest integer?
Solution:
Given that the die has 6 faces marked by the given numbers as below:
![]()
When a die is rolled, total number of possible outcomes – 6
(i) For getting a positive integer, the favourable outoomes are: 1, 2, 3
⇒ Number of favourable outcomes – 3
⇒ Required probability = \(\frac { 3 }{ 6 } =\frac { 1 }{ 2 } \)
(ii) For getting an integer greater than -3, the favourable outcomes
are: -2,-1, 1, 2, 3
⇒ Number of favourable outcomes – 5
⇒ Required probability = \(\frac { 5 }{ 6 } \)
(iii) For getting a smallest integer, the favourable outoomes are: -3
⇒ Number of favourable outcomes = 1
⇒ Required probability = \(\frac { 1 }{ 6 } \)
Question 34.
A bag contains 5 white balls, 6 red balls and 9 green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is:
(i) a green ball
(ii) a white or a red ball.
(iii)Neither a green ball nor a white ball
Solution:
Number of white balls = 5
Number of red balls = 6
Number of green balls = 9
∴ Total number of balls = 5 + 6 + 9 = 20

Question 35.
A game of numbers has cards marked with 11, 12, 13, ….., 40. A card is drawn at random. Find the probability that the number on the card drawn is:
(i) A perfect square
(ii) Divisible by 7.
Solution:
Total number of outcomes = 30
(i) The perfect squares from 11 to 40 are 16, 25 and 36. So, the number of possible outcomes = 3 Hence, the probability that the number on the card drawn is a perfect square
= \(=\quad \frac { Number\quad of\quad possible\quad outcomes }{ Total\quad number\quad of\quad outcomes } =\frac { 3 }{ 30 } =\frac { 1 }{ 10 } \)
(ii) Among the given numbers, 14, 21, 28 and 35 are divisible by 7. So, the number of possible outcomes = 4 Hence, the probability that the number on the card drawn is divisible by 7
= \(\frac{\text { Number of possible autoomes }}{\text { Total number of outoomes }}=\frac{4}{30}=\frac{2}{15}\)
Question 36.
Sixteen cards are labelled as a, b, c, … , m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is:
i. a vowel
ii. a consonant
iii. none of the letters of the word median?
Solution:
Here, Total number of all possible outcomes = 16
i. a, e, i and o are the vowels.
Number of favourable outcomes = 4
∴ Required Probability = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of all possible outcomes }}=\frac{4}{16}=\frac{1}{4}\)
ii. Number of consonants = 16 – 4 (vowels) = 12
∴ Number of favourable outcomes = 12
∴ Required Probability = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of all possible outcomes }}=\frac{12}{16}=\frac{3}{4}\)
iii. Median contains 6 letters.
∴ Number of favourable outcomes = 16 – 6 = 10
∴ Required Probability = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of all possible outcomes }}=\frac{10}{16}=\frac{5}{8}\)
Question 37.
A box contains a certain number of balls. On each of 60% balls, letter A is marked. On each of 30% balls, letter B is marked and on each of remaining balls, letter C is marked. A ball is drawn from the box at random. Find the probability that the ball drawn is:
i. marked C
ii. A or B
iii. neither B nor C
Solution:
A box contains,
60% balls, letter A is marked.
30% balls, letter B is marked.
10% balls, letter C is marked.
i. Total number of all possible outcomes = 100
Number of favourable outcomes = 10
∴ Required Probability = \(\frac{\text { Number of favou rable outcomes }}{\text { Total number of all possible outcomes }}=\frac{10}{100}=\frac{1}{10}\)
ii. The probability that the ball drawn is marked A = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of all possible outcomes }}=\frac{60}{100}=\frac{6}{10}\) … (1)
The probability that the ball drawn is marked B = \(\frac{\text { Number of favou rable outcomes }}{\text { Total number of all possible outcomes }}=\frac{30}{100}=\frac{3}{10}\) … (2)
∴ Required Probability = \(\frac{6}{10}+\frac{3}{10}=\frac{9}{10}\)
iii. The probability that the ball drawn is neither B nor C
= 1 – [P(B) + P(C)]
= 1 – \(\left[\frac{3}{10}+\frac{1}{10}\right]\)
= 1 – \(\frac{4}{10}\)
= \(\frac{6}{10}\)
= \(\frac{3}{5}\)
Question 38.
A box contains a certain number of balls. Some of these balls are marked A, some are marked B and the remaining are marked C. When a ball is drawn at random from the box P(A) = \(\frac{1}{3}\) and P(B) = \(\frac{1}{4}\). If there are 40 balls in the box which are marked C, find the number of balls in the box.
Solution:
P(C) = 1 – [P(A) + P(B)] = \(1-\left[\frac{1}{3}+\frac{1}{4}\right]=1-\frac{7}{12}=\frac{5}{12}\)
Probability = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of all possible outcomes }}\)
Given that 40 balls in the box are marked C.
⇒ \(\frac{5}{12}=\frac{40}{\text { Total number of all possible outcomes }}\)
⇒ Total number of all possible outcomes = \(\frac{40 \times 12}{5}=96\)
∴ the number of balls in the box is 96.
More Resources for Selina Concise Class 10 ICSE Solutions






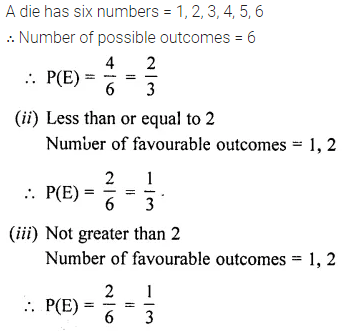








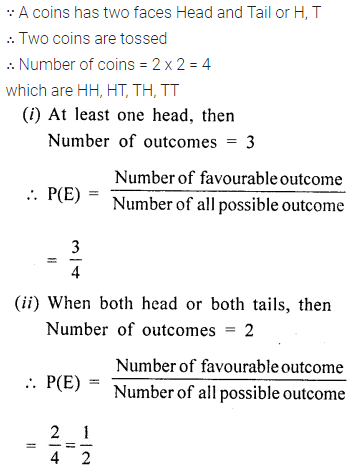




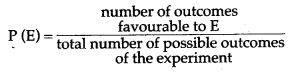


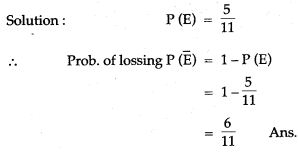



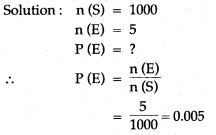




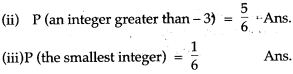













 In Venn Diagrams, we learned that an element was in the intersection “A and B”, only when the element was in BOTH sets.
In Venn Diagrams, we learned that an element was in the intersection “A and B”, only when the element was in BOTH sets. In Venn Diagrams, we learned that an element was in the union “A or B”, when the element was in either or both sets.
In Venn Diagrams, we learned that an element was in the union “A or B”, when the element was in either or both sets.

