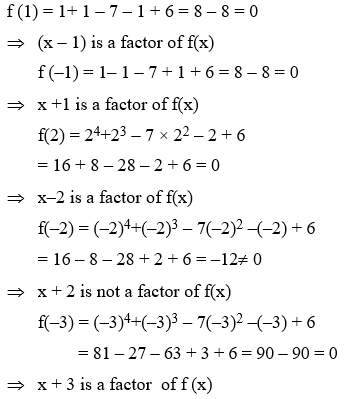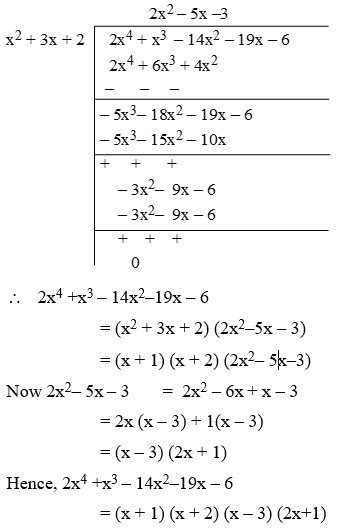Relationship Between Zeros And Coefficients Of A Polynomial
Consider quadratic polynomial
P(x) = 2x2 – 16x + 30.
Now, 2x2 – 16x + 30 = (2x – 6) (x – 3)
= 2 (x – 3) (x – 5)
The zeros of P(x) are 3 and 5.
Sum of the zeros = 3 + 5 = 8 = \(\frac { -\left( -16 \right) }{ 2 } \) = \(\text{-}\left[ \frac{\text{coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
Product of the zeros = 3 × 5 = 15 = \(\frac { 30 }{ 2 }\) = \(\left[ \frac{\text{constant term }}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
So if ax2 + bx + c, a ≠ 0 is a quadratic polynomial and α, β are two zeros of polynomial then
\(\alpha +\beta =-\frac { b }{ a } \)
\(\alpha \beta =\frac { c }{ a } \)
In general, it can be proved that if α, β, γ are the zeros of a cubic polynomial ax3 + bx2 + cx + d, then
\(\alpha +\beta +\gamma =\frac { -b }{ a } \)
\( \alpha \beta +\beta \gamma +\gamma \alpha =\frac { c }{ a } \)
\( \alpha \beta \gamma =\frac { -d }{ a } \)
Note: \(\frac { b }{ a } \), \(\frac { c }{ a }\) and \(\frac { d }{ a } \) are meaningful because a ≠ 0.
Relationship Between Zeros And Coefficients Of A Polynomial Example Problems With Solutions
Example 1: Find the zeros of the quadratic polynomial 6x2 – 13x + 6 and verify the relation between the zeros and its coefficients.
Sol. We have, 6x2 – 13x + 6 = 6×2 – 4x – 9x + 6
= 2x (3x – 2) –3 (3x – 2)
= (3x – 2) (2x – 3)
So, the value of 6x2 – 13x + 6 is 0, when
(3x – 2) = 0 or (2x – 3) = 0 i.e.,
When x = \(\frac { 2 }{ 3 } \) or \(\frac { 3 }{ 2 } \)
Therefore, the zeros of 6x2 – 13x + 6 are
\(\frac { 2 }{ 3 } \) and \(\frac { 3 }{ 2 } \)
Sum of the zeros
= \(\frac { 2 }{ 3 } \) + \(\frac { 3 }{ 2 } \) = \(\frac { 13 }{ 6 } \) = \(\frac { \left( -13 \right) }{ 6 } \) = \(\text{-}\left[ \frac{\text{coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
Product of the zeros
= \(\frac { 2 }{ 3 } \) × \(\frac { 3 }{ 2 } \) = \(\frac { 6 }{ 6 } \) = \(\left[ \frac{\text{constant term }}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
Example 2: Find the zeros of the quadratic polynomial 4x² – 9 and verify the relation between the zeros and its coefficients.
Sol. We have,
4x2 – 9 = (2x)2 – 32 = (2x – 3) (2x + 3)
So, the value of 4x2 – 9 is 0, when
2x – 3 = 0 or 2x + 3 = 0
i.e., when x = \(\frac { 3 }{ 2 } \) or x = \(\frac { -3 }{ 2 } \).
Therefore, the zeros of 4x2 – 9 are \(\frac { 3 }{ 2 } \) & \(\frac { -3 }{ 2 } \).
Sum of the zeros
= \(\frac { 3 }{ 2 }\) \(-\frac { 3 }{ 2 } \) = 0 = \(-\frac { \left( 0 \right) }{ 4 } \) = \(\text{-}\left[ \frac{\text{coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
Product of the zeros
= \(\frac { 3 }{ 2 }\) × \(\frac { -3 }{ 2 }\) = \(\frac { -9 }{ 4 }\) = \(\left[ \frac{\text{constant term }}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
Example 3: Find the zeros of the quadratic polynomial 9x2 – 5 and verify the relation between the zeros and its coefficients.
Sol. We have,
9x2 – 5 = (3x)2 – (√5)2 = (3x – √5) (3x + √5)
So, the value of 9x2 – 5 is 0,
when 3x – √5 = 0 or 3x + √5 = 0
i.e., when x = \(\frac { \sqrt { 5 } }{ 3 } \) or x = \(\frac { -\sqrt { 5 } }{ 3 } \).
Sum of the zeros
= \(\frac { \sqrt { 5 } }{ 3 } \) \(-\frac { \sqrt { 5 } }{ 3 } \) = 0 = \(-\frac { \left( 0 \right) }{ 9 } \) = \(\text{-}\left[ \frac{\text{coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
Product of the zeros
= \(\left( \frac { \sqrt { 5 } }{ 3 } \right) \) × \(\left( \frac { -\sqrt { 5 } }{ 3 } \right) \) = \(\frac { -5 }{ 9 } \) = \(\left[ \frac{\text{constant term }}{\text{coefficient of }{{\text{x}}^{\text{2}}}} \right]\)
Example 4: If α and β are the zeros of ax2 + bx + c, a ≠ 0 then verify the relation between the zeros and its coefficients.
Sol. Since a and b are the zeros of polynomial ax2 + bx + c.
Therefore, (x – α), (x – β) are the factors of the polynomial ax2 + bx + c.
⇒ ax2 + bx + c = k (x – α) (x – β)
⇒ ax2 + bx + c = k {x2 – (α + β) x + αβ}
⇒ ax2 + bx + c = kx2 – k (α + β) x + kαβ …(1)
Comparing the coefficients of x2, x and constant terms of (1) on both sides, we get
a = k, b = – k (α + β) and c = kαβ
⇒ α + β = \(\frac { -b }{ k } \) and αβ = \(\frac { c }{ k } \)
α + β = \(\frac { -b }{ a } \) and αβ = \(\frac { c }{ a } \) [∵ k = a]
Sum of the zeros = \(\frac { -b }{ a } \) = \(\frac{\text{- coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}\)
Product of the zeros = \(\frac { c }{ a } \) = \(\frac{\text{constant term }}{\text{coefficient of }{{\text{x}}^{\text{2}}}}\)
Example 5: Prove relation between the zeros and the coefficient of the quadratic polynomial
ax2 + bx + c.
Sol. Let a and b be the zeros of the polynomial ax2 + bx + c
α = \(\frac{-b+\sqrt{{{b}^{2}}-4ac}}{2a}\) ….(1)
β = \(\frac{-b-\sqrt{{{b}^{2}}-4ac}}{2a}\) ….(2)
By adding (1) and (2), we get
α + β = \(\frac{-b+\sqrt{{{b}^{2}}-4ac}}{2a}\) + \(\frac{-b-\sqrt{{{b}^{2}}-4ac}}{2a}\)
= \(\frac{ -2b }{ 2a } \) = \(\frac{ -b }{ a } \) = \(\frac{\text{- coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}\)
Hence, sum of the zeros of the polynomial
ax2 + bx + c is \(\frac{ -b }{ a } \)
By multiplying (1) and (2), we get
αβ = \(\frac{-b+\sqrt{{{b}^{2}}-4ac}}{2a}\) × \(\frac{-b-\sqrt{{{b}^{2}}-4ac}}{2a}\)
= \(\frac{{{b}^{2}}-{{b}^{2}}+4ac}{4{{a}^{2}}}\)
= \(\frac{4ac}{4{{a}^{2}}}\) = \(\frac{ c }{ a } \)
= \(\frac{\text{constant term }}{\text{coefficient of }{{\text{x}}^{\text{2}}}}\)
Hence, product of zeros = \(\frac{ c }{ a } \)
Example 6: find the zeroes of the quadratic polynomial x2 – 2x – 8 and verify a relationship between zeroes and its coefficients.
Sol. x2 – 2x – 8 = x2 – 4x + 2x – 8
= x (x – 4) + 2 (x – 4) = (x – 4) (x + 2)
So, the value of x2 – 2x – 8 is zero when
x – 4 = 0 or x + 2 = 0 i.e., when x = 4 or x = – 2.
So, the zeroes of x2 – 2x – 8 are 4, – 2.
Sum of the zeroes
= 4 – 2 = 2 = \(-\frac { \left( -2 \right) }{ 1 } \) = \(\frac{\text{- coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}\)
Product of the zeroes
= 4 (–2) = –8 = \(\frac { -8 }{ 1 } \) = \(\frac{\text{constant term }}{\text{coefficient of }{{\text{x}}^{\text{2}}}}\)
Example 7: Verify that the numbers given along side of the cubic polynomials are their zeroes. Also verify the relationship between the zeroes and the coefficients. 2x3 + x2 – 5x + 2 ; , 1, – 2
Sol. Here, the polynomial p(x) is 2x3 + x2 – 5x + 2
Value of the polynomial 2x3 + x2 – 5x + 2
when x = 1/2
= \(2{{\left( \frac{1}{2} \right)}^{3}}+{{\left( \frac{1}{2} \right)}^{2}}-5\left( \frac{1}{2} \right)+2\) = \(\frac{1}{4}+\frac{1}{4}-\frac{5}{2}+2\) = 0
So, 1/2 is a zero of p(x).
On putting x = 1 in the cubic polynomial
2x3 + x2 – 5x + 2
= 2(1)3 + (1)2 –¬ 5(1) + 2 = 2 + 1 – 5 + 2 = 0
On putting x = – 2 in the cubic polynomial
2x3 + x2 – 5x + 2
= 2(–2)3 + (–2)2 – 5 (–2) + 2
= – 16 + 4 + 10 + 2 = 0
Hence, \(\frac{ 1 }{ 2 } \), 1, – 2 are the zeroes of the given polynomial.
Sum of the zeroes of p(x)
= \(\frac{ 1 }{ 2 } \) + 1 – 2 = \(\frac{ -1 }{ 2 } \) = \(\frac{-\text{ coefficient of }{{x}^{2}}}{\text{coefficient of }{{x}^{3}}}\)
Sum of the products of two zeroes taken at a time
= \(\frac{ 1 }{ 2 } \) × 1 + \(\frac{ 1 }{ 2 } \) × (–2) + 1 × (–2)
= \(\frac{ 1 }{ 2 } \) – 1 – 2 = \(\frac{ -5 }{ 2 } \) = \(\frac{\text{coefficient of }x}{\text{coefficient of }{{x}^{3}}}\)
Product of all the three zeroes
= \(\frac{ 1 }{ 2 } \) × (1) × (–2) = –1
= \(\frac{ -2 }{ 2 } \) = \(\frac{-\text{ constant term }}{\text{coefficient of }{{x}^{3}}}\)