Linear Equations

Solution Of A Linear Equation In Two Variables

by

Solution Of A Linear Equation In Two Variables Example Problems With Solutions

Method: Put the value of x (or y) = 0, ±1, ±2, ±3,……, we get values of y (or x). By this we can find many solutions of given equation.

Read More:

Example 1:    Find five solutions of
(i) 2x + 3y = 6          (ii) 3x – 2y = 12         (iii) 7x + y = 15
Solution:    (i) 2x = 6 – 3y
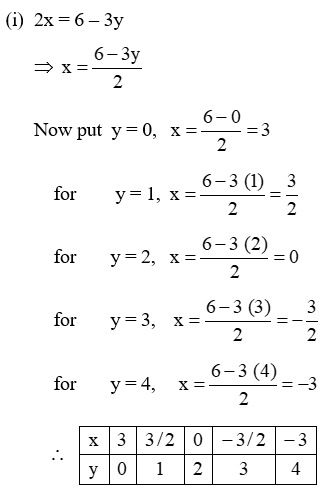
Solution Of A Linear Equation In Two Variables 1
Solution Of A Linear Equation In Two Variables 2

Example 2:    Find two solutions of
(i) 3x – 7y = 21 (ii) 8x – 5y = 16
Solution:    (i) 3x – 7y = 21
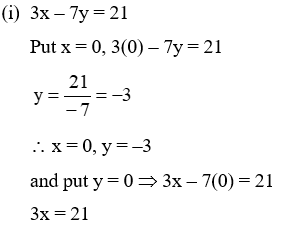
Solution Of A Linear Equation In Two Variables 3
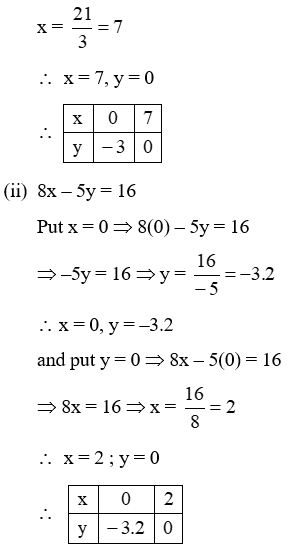
Solution Of A Linear Equation In Two Variables 4

Example 3:    Find five solutions of
(i) 3x = 5             (ii) 7y = 10
Solution:    (i) The equation is only in one variable. So we have to convert into 2 variable 3x + 0.y = 5
Solution Of A Linear Equation In Two Variables 5
Note:
Ordered Pair: If value of x & y are represent in form (x, y) then this form is called ordered pair form : Eg. x = 5, y = 7/3 then ordered pair form = (5, 7/3). First part is called abscissa (x part) and second part is ordinate (y part).

Example 4:    Check the following value of x & y are solution of equation 9x – 8y = 72 or not
(i) (0, 9)               (ii) (0, – 9)               (iii) (– 8, 0)
(iv) (+8, 0)           (v) (1, 1)                    (vi) (1/3, 1/2)
Solution:    Given equation 9x – 8y = 72
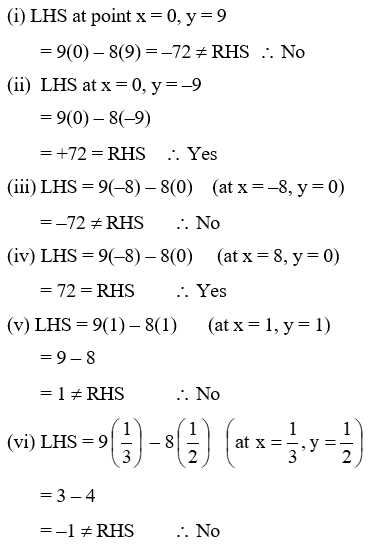
Solution Of A Linear Equation In Two Variables 6

Example 5:    Find the value of k in equation 2x + ky = 6 if (–2, 2) is a solution.
Solution:    ∵ (–2, 2) is a solution of 2x + ky = 5
∴ 2(–2) + k(2) = 6
– 4 + 2k = 6 ⇒ 2k = 6 + 4
k = 10/2 = 5

Example 6:    Find value of p if (4, –4) is a solution of x – py = 8.
Solution:    x – py = 8
4 – p (–4) = 8
4p = 8 – 4
4p = 4
p = 1

Example 7:    Find the value of a if (a, –3a) is a solution of 14x + 3y = 35.
Solution:    Put x = a and y = –3a in given equation
14(a) + 3(–3a) = 35
14a – 9a = 35
5a = 35
a = 7

 

Linear Equations In One Variable

by

Linear Equations In One Variable

A statement of equality of two algebraic expressions, which involve one or more unknown quantities is known as an equation.
A linear equation is an equation which involves linear polynomials.
A value of the variable which makes the two sides of the equation equal is called the solution of the equation.
Same quantity can be added/subtracted to/from both the sides of an equation without changing the equality.
Both the sides of an equation can be multiplied/divided by the same non-zero number without changing the equality.

GENERAL FORM OF LINEAR EQUATION IN TWO VARIABLES

ax + by + c = 0, a ≠ 0, b ≠ 0 or any one from a & b can zero.

Read More:

General Form Of Linear Equation In Two Variables Example Problems With Solutions

Example 1:    Express the following linear equations in general form and identify coefficients of x, y and constant term.
Solution:
General-Form-Of-Linear-Equation-In-Two-Variables
Make linear equation by the following statements:

Example 2:     The cost of 2kg of apples and 1 kg of grapes on a day was found to be 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is 300. Represent the situation algebraically.
Solution:    Let cost of per kg apples & grapes are x & y respectively then by Ist condition:
2x + y = 160       ……(i)
& by IInd condition: 4x + 2y = 300         …..(ii)

Example 3:    The coach of a cricket team buys 3 bats and 6 balls for 3900. Later, she buys another bat and 3 more balls of the same kind for 1300. Represent this situation algebraically.
Solution:    Let cost of a bat and a ball are x & y respectively. According to questions
3x + 6y = 3900        …..(i)
& x + 3y = 1300       …..(ii)

https://www.youtube.com/watch?v=fB1evicj5po

Example 4:    10 students of class IX took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys.
Solution:    Let no. of boys and girls are x & y then according to question
x + y = 10          ……(i)
& y = x + 4         ……(ii)

Example 5:    Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is
36 m.
Solution:     Let length & breadth are x m and y m.
∴ according to question 1/2 perimeter = 36
1/2 [2(l + b)] = 36
⇒ x + y = 36        …..(i)
also length = 4 + breadth
x = 4 + y         ..…(ii)

Example 6:     The difference between two numbers is 26 and one number is three times the other.
Solution:    Let the numbers are x and y & x > y
∴ x – y = 26       ……(i)
and  x = 3y ……(ii)

Example 7:    The larger of two supplementary angles exceeds the smaller by 18 degrees.
Solution:    Sol. Let the two supplementary angles are x and y & x > y
Then x + y = 180°    ……(i)
and   x = y + 18°       ……(ii)

Example 8:    A fraction becomes 9/11, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 5/6.
Solution:    Let fraction is x/y
Now according to question    \(\frac{x+2}{y+2}=\frac{9}{11}\)
⇒ 11x + 22 = 9y + 18
⇒ 11x – 9y = – 4          …..(i)
and
\(\frac{x+3}{y+3}=\frac{5}{6}\)
⇒ 6x + 18 = 5y + 15
⇒ 6x – 5y = –3           ….(ii)

Example 9:    Five years hence, the age of Sachin will be three times that of his son. Five years ago, Sachin’s age was seven times that of his son.
Solution:    Let present ages of Sachin & his son are
x years and y years.
Five years hence,
age of Sachin = (x + 5) years & his son’s age = (y + 5) years
according to question (x + 5) = 3(y + 5)
⇒ x + 5 = 3y + 15
⇒ x – 3y = 10          ……(i)
and 5 years ago age of both were (x – 5) years and (y – 5) years respectively
according to question (x – 5) = 7(y – 5)
⇒ x – 5 = 7y – 35
⇒ x – 7y = –30      .…(ii)

 

Equations Of Lines Parallel To The X-Axis And Y-Axis

by

Equations Of Lines Parallel To The X-Axis And Y-Axis

We can represent graph of these equations in two types of geometrically
(A) in one variable or on number line
(B) in two variable or on the Cartesian plane
In one variable, the solution is represent by a point. While in two variable, the solution is represent by a line parallel to x or y axis.

Equations Of Lines Parallel To The X-Axis And Y-Axis Example Problems With Solutions

Example 1:    Give the geometric representation of x = 5 as an equation in
(i) one variable
(ii) two variable
(iii) also find the common solution of x = 5 & x = 0
Solution:    (i) x = 5
It is in only one variable so representation on number line
Equations-Of-Lines-Parallel-To-The-X-Axis-And-Y-Axis-Example-1
(ii) In two variables (or on Cartesian plane)
first we have to represent equation in two variables x + 0.y = 5         …..(i)
now we have to find two or three solutions of equations (i)

x555
y012

Then mark these points on graph with proper scale & join them
Equations-Of-Lines-Parallel-To-The-X-Axis-And-Y-Axis-Example-1-1
Scale: on both axis 10 lines or 1 big box = 1 cm
(iii)  ∵  x = 5 is line parallel to y axis and x = 0 is y axis.
∴ both are parallel
∴ no common solution

Example 2:    Give geometric representation of 5x + 7 = 0 as an equation
(i) in one variable (or on a number line)
(ii) in two variable (or on Cartesian plane)
Solution:    (i) 5x + 7 = 0
⇒ 5x = –7
⇒ x = –7/5
= – 1.4
Equations-Of-Lines-Parallel-To-The-X-Axis-And-Y-Axis-Example-2
(ii) 5x + 0.y = –7

x-7/5-7/5-7/5

-7/5

y

012

3

Equations-Of-Lines-Parallel-To-The-X-Axis-And-Y-Axis-Example-2-1
Scale : on both axis 10 lines or 1 box = 1 cm
Note:
If constant term ‘c’ is zero in equation
ax + by + c = 0 then line will pass through origin (always)
Equations-Of-Lines-Parallel-To-The-X-Axis-And-Y-Axis-Example-2-2