Conic Sections
Definition:
The curves obtained by intersection of a plane and a double cone in different orientation are called conic section.

Definitions of various important terms:
- Focus: The fixed point is called the focus of the conic-section.
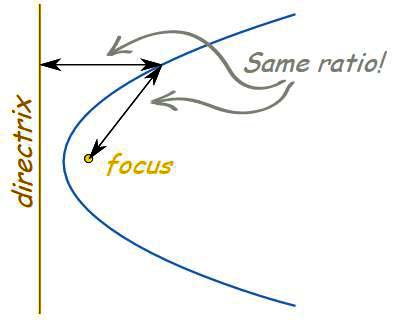
- Directrix: The fixed straight line is called the directrix of the conic section.
- Eccentricity: The constant ratio is called the eccentricity of the conic section and is denoted by e.
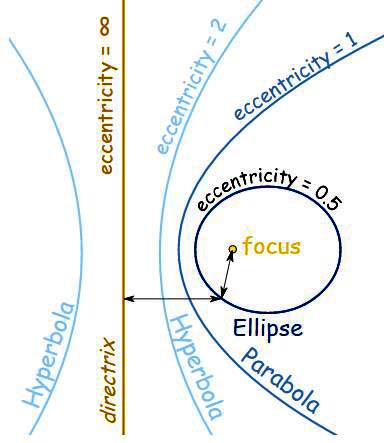
- Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section. A conic is always symmetric about its axis.
- Vertex: The points of intersection of the conic section and the axis are called vertices of conic section.
- Centre: The point which bisects every chord of the conic passing through it, is called the centre of conic.
- Latus-rectum: The latus-rectum of a conic is the chord passing through the focus and perpendicular to the axis.
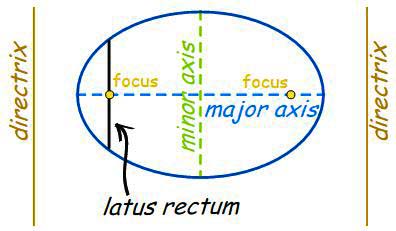
- Double ordinate: The double ordinate of a conic is a chord perpendicular to the axis.
- Focal chord: A chord passing through the focus of the conic is called a focal chord.
- Focal distance: The distance of any point on the conic from the focus is called the focal distance of the point.
General equation of a conic section when its focus, directrix and eccentricity are given:
Let S(α, β) be the focus, Ax + By + C = 0 be the directrix and e be the eccentricity of a conic.
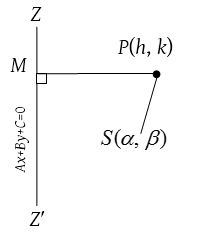 Let P(h, k) be any point on the conic. Let PM be the perpendicular from P, on the directrix. Then by definition,
Let P(h, k) be any point on the conic. Let PM be the perpendicular from P, on the directrix. Then by definition,
SP = ePM ⇒ SP2 = e2PM2
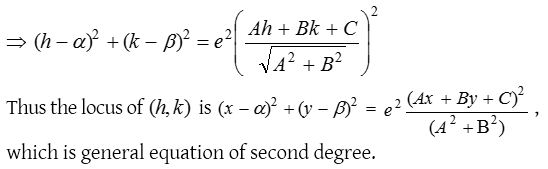
Recognisation of conics
The equation of conics is represented by the general equation of second degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ……(i)
and discriminant of above equation is represented by ∆, where ∆ = abc + 2fgh – af2 – bg2 – ch2
Case I: When ∆ = 0.
In this case equation (i) represents the degenerate conic whose nature is given in the following table.
| S. No. | Condition | Nature of conic |
| 1. | ∆ = 0 and ab – h2 = 0 | A pair of coincident straight lines |
| 2. | ∆ = 0 and ab – h2 < 0 | A pair of intersecting straight lines |
| 3. | ∆ = 0 and ab – h2 > 0 | A point |
Case II: When ∆ ≠ 0.
In this case equation (i) represents the non-degenerate conic whose nature is given in the following table.
| S. No. | Condition | Nature of conic |
| 1. | ∆ ≠ 0, h = 0, a = b, e = 0 | A circle |
| 2. | ∆ ≠ 0, ab – h2 = 0, e = 1 | A parabola |
| 3. | ∆ ≠ 0, ab – h2 > 0, e < 0 | An ellipse |
| 4. | ∆ ≠ 0, ab – h2 < 0, e > 0 | A hyperbola |
| 5. | ∆ ≠ 0, ab – h2 < 0, a + b = 0, e = √2 | A rectangular hyperbola |