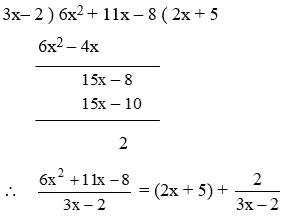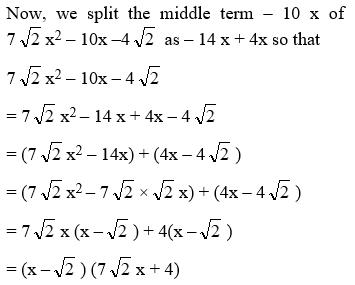Factorization Of Polynomials

Factorization Of Polynomials Using Factor Theorem

by

Factorization Of Polynomials Using Factor Theorem

Factor Theorem:

If p(x) is a polynomial of degree n  1 and a is any real number, then (i) x – a is a factor of p(x), if p(a) = 0, and (ii) p(a) = 0, if x – a is a factor of p(x).
Proof: By the Remainder Theorem,
p(x) = (x – a) q(x) + p(a).
(i) If p(a) = 0, then p(x) = (x – a) q(x), which shows that x – a is a factor of p(x).
(ii) Since x – a is a factor of p(x),
p(x) = (x – a) g(x) for same polynomial g(x). In this case, p(a) = (a – a) g(a) = 0.

  1. Obtain the polynomial p(x).
  2. Obtain the constant term in p(x) and find its all possible factors. For example, in the polynomial
    x4 + x3 – 7x2 – x + 6 the constant term is 6 and its factors are ± 1, ± 2, ± 3, ± 6.
  3. Take one of the factors, say a and replace x by it in the given polynomial. If the polynomial reduces to zero, then (x – a) is a factor of polynomial.
  4. Obtain the factors equal in no. to the degree of polynomial. Let these are (x–a), (x–b), (x–c.)…..
  5. Write p(x) = k (x–a) (x–b) (x–c) ….. where k is constant.
  6. Substitute any value of x other than a,b,c …… and find the value of k.

People also ask

Factorization Of Polynomials Using Factor Theorem Example Problems With Solutions

Example 1:    Factorize x2 +4 + 9 z2 + 4x – 6 xz – 12 z
Solution:
The presence of the three squares viz.x2, (2)2, and (3z)2 gives a clue that identity (vii) could be used. So we write.
A = x2 + (2)2 + (3z)2 + 4x – 6 xz – 12 z
We note that the last two of the product terms are negative and that both of these contain z. Hence we write A as
A = x2 + (2)2 + (–3z)2 + 2.2x – 2.x.(–3z) + 2.2 (– 3z)
= (x+2 – 3z)2
= (x + 2 – 3z) (x + 2 – 3z)

Example 2:    Using factor theorem, factorize the polynomial x3 – 6x2 + 11 x – 6.
Solution:
Let f(x) = x3 – 6x2 + 11x – 6
The constant term in f(x) is equal to – 6 and factors of – 6 are ±1, ± 2, ± 3, ± 6.
Putting x = 1 in f(x), we have
f(1) = 13 – 6 ×12 + 11× 1– 6
= 1 – 6 + 11– 6 = 0
∴ (x– 1) is a factor of f(x)
Similarly, x – 2 and x – 3 are factors of f(x).
Since f(x) is a polynomial of degree 3. So, it can not have more than three linear factors.
Let f(x) = k (x–1) (x– 2) (x – 3). Then,
x3– 6x2 + 11x – 6 = k(x–1) (x– 2) (x– 3)
Putting x = 0 on both sides, we get
– 6 = k (0 – 1) (0 – 2) (0 – 3)
⇒ – 6 = – 6 k ⇒ k = 1
Putting k = 1 in f(x) = k (x– 1) (x– 2) (x–3), we get
f(x) = (x–1) (x– 2) (x – 3)
Hence, x3–6x2 + 11x – 6 = (x– 1) (x – 2) (x–3)

Example 3:    Using factor theorem, factorize the polynomial x4 + x3 – 7x2 – x + 6.
Solution:
Let f(x) = x4 + x3– 7x2 –x + 6
the factors of constant term in f(x) are ±1, ±2, ±3 and ± 6
Now,
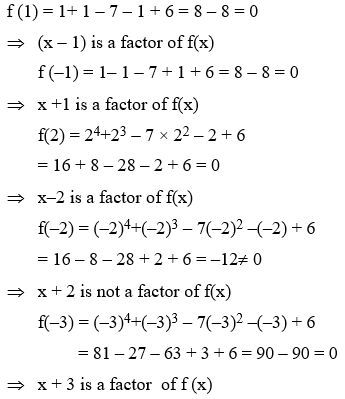
Factorization Of Polynomials Using Factor Theorem 1
Since f(x) is a polynomial of degree 4. So, it cannot have more than 4 linear factors
Thus, the factors of f (x) are (x–1), (x+1),
(x–2) and (x+3).
Let f(x) = k (x–1) (x+1) (x–2) (x + 3)
⇒ x4 + x3 – 7x2 – x + 6
= k (x–1) (x +1) (x – 2) (x + 3)
Putting x = 0 on both sides, we get
6 = k (–1) (1) (–2) (3) ⇒ 6 = 6 k ⇒ k = 1
Substituting k = 1 in (i), we get
x4 + x3 – 7x2 – x + 6 = (x–1) (x +1) (x–2) (x+3)

Example 4:    Factorize,  2x4 + x3 – 14x2 – 19x – 6
Solution:
Let f(x) = 2x4 + x3 – 14x2 – 19x – 6 be the given polynomial. The factors of the constant term – 6 are ±1, ±2, ±3 and ±6, we have,
f(–1) = 2(–1)4 + (–1)3 – 14(–1)2 – 19(–1)– 6
= 2 – 1 – 14 + 19 – 6 = 21 – 21 = 0
and,
f(–2) = 2(–2)4 + (–2)3 – 14(–2)2 – 19(–2)– 6
= 32 – 8 – 56 + 38 – 6 = 0
So, x + 1 and x + 2 are factors of f(x).
⇒ (x + 1) (x + 2) is also a factor of f(x)
⇒ x2 + 3x + 2 is a factor of f(x)
Now, we divide
f(x) = 2x4 +x3 – 14x2–19x – 6 by
x2 + 3x + 2 to get the other factors.
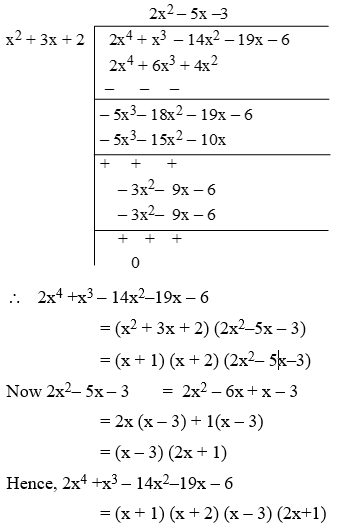
Factorization Of Polynomials Using Factor Theorem 2

Example 5:    Factorize,  9z3 – 27z2 – 100 z+ 300, if it is given that (3z+10) is a factor of it.
Solution:
Let us divide 9z3 – 27z2 – 100 z+ 300 by
3z + 10 to get the other factors
Factorization Of Polynomials Using Factor Theorem 3
∴ 9z3 – 27z2 – 100 z+ 300
= (3z + 10) (3z2–19z + 30)
= (3z + 10) (3z2–10z – 9z + 30)
= (3z + 10) {(3z2–10z) – (9z – 30)}
= (3z + 10) {z(3z–10) – 3(3z–10)}
= (3z + 10) (3z–10) (z–3)
Hence, 9z3–27z2–100z+ 300
= (3z + 10) (3z–10) (z–3)

Example 6:    Simplify
\(\frac{4x-2}{{{x}^{2}}-x-2}+\frac{3}{2{{x}^{2}}-7x+6}-\frac{8x+3}{2{{x}^{2}}-x-3}\)
Solution:
Factorization Of Polynomials Using Factor Theorem 4

Example 7:    Establish the identity
\(\frac{6{{x}^{2}}+11x-8}{3x-2}=\left( 2x+5 \right)+\frac{2}{3x-2}\)
Solution:
Factorization Of Polynomials Using Factor Theorem 5

How To Factorise A Polynomial By Splitting The Middle Term

by

Factorise A Polynomial By Splitting The Middle Term Example Problems With Solutions

Type I: Factorization of Quadratic polynomials of the form x2 + bx + c.
(i) In order to factorize x2 + bx + c we have to find numbers p and q such that p + q = b and pq = c.
(ii) After finding p and q, we split the middle term in the quadratic as px + qx and get desired factors by grouping the terms.

Example 1:    Factorize each of the following expressions:
(i) x2 + 6x + 8               (ii) x2 + 4x –21
Solution:
(i) In order to factorize x2  + 6x + 8, we find two numbers p and q such that p + q = 6 and pq = 8.
Clearly, 2 + 4 = 6 and 2 × 4 = 8.
We know split the middle term 6x in the given quadratic as 2x + 4x, so that
x2    + 6x + 8 = x2  + 2x + 4x + 8
= (x2  + 2x) + (4x + 8)
= x (x + 2) + 4 (x+ 2)
= (x + 2) (x + 4)
(ii) In order to factorize x2  + 4x – 21, we have to find two numbers p and q such that
p + q = 4 and pq = – 21
Clearly, 7 + (– 3) = 4 and 7 × – 3 = – 21
We now split the middle term 4x of
x2  + 4x – 21 as 7x – 3x, so that
x2  + 4x – 21 = x2  + 7x – 3 x – 21
= (x2  + 7x) – (3x + 21)
= x (x + 7) – 3 (x + 7) = (x + 7) (x – 3)

Example 2:    Factorize each of the following quadratic polynomials:   x2 – 21x + 108
Solution:    In order to factorize x2 – 21x + 108,
we have to find two numbers such that their sum is – 21 and the product 108.
Clearly, – 21 = – 12– 9 and – 12 × – 9 = 108
x2 – 21 x + 108 = x2 – 12 x – 9x + 108
= (x2 – 12 x) – (9x– 108)
= x(x – 12) – 9 (x – 12) = (x–12) (x – 9)

Example 3:    Factorize the following by splitting the middle term :  x2 + 3 √3 x + 6
Solution:    In order to factorize x2 + 3 √3 x + 6, we have to find two numbers p and q such that
How To Factorise A Polynomial By Splitting The Middle Term 1

Type II: Factorization of polynomials reducible to the form x2 + bx + c.

Example 4:    Factorize (a2 – 2a)2 – 23(a2 – 2a) + 120.
Solution:
How To Factorise A Polynomial By Splitting The Middle Term 2

Example 5:    Factorize the following by splitting the middle term x4– 5x2 + 4
Solution:
Let x2 = y. Then, x4 – 5x2 + 4
= y2 – 5 y + 4
Now, y2 – 5 y + 4
= y2 – 4y – y + 4
= (y2 – 4y) – (y – 4)
= y(y –4) – (y– 4)
= (y – 4) (y – 1)
Replacing y by x2 on both sides, we get
x4 – 5x2 + 4 = (x2–4) (x2 – 1)
= (x2–22) (x2 – 12) = (x–2) (x+2) (x – 1) (x + 1)

Example 6:    Factorize (x2 – 4x) (x2 – 4x – 1) – 20
Solution:
The given expression is
(x2 – 4x) (x2 – 4x – 1) – 20
= (x2 – 4x)2 – (x2 – 4x) – 20
Let x2 – 4x = y . Then,
(x2 – 4x)2 – (x2 – 4x) – 20 = y2 – y – 20
Now, y2 – y – 20
= y2 –5 y + 4y – 20
= (y2 – 5 y) + (4y– 20)
= y (y – 5) + 4 (y – 5)
= (y – 5) (y + 4)
Thus, y2 – y – 20 = (y – 5) (y + 4)
Replacing y by x2 – 4x on both sides, we get
(x2 – 4x)2 – (x2 – 4x) – 20
= (x2 – 4x – 5) (x2 – 4x +4)
= (x2 – 5x + x – 5) (x2 – 2 × x × 2 + 22)
= {x (x – 5) + (x – 5)} (x – 2)2
= (x – 5) (x + 1) (x – 2)2

Type III: Factorization of Expressions which are not quadratic but can factorized by splitting the middle term.

Example 7:    If x2 + px + q = (x + a) (x + b), then factorize x2 + pxy + qy2.
Solution:    We have,
x2 + px + q = (x + a) (x + b)
⇒ x2 + px + q = x2 + x(a + b) + ab
On equating the coefficients of like powers of x, we get
p = a + b and q = ab
∴ x2 + pxy + qy2 = x2 + (a + b)xy + aby2
= (x2 + axy) + (bxy + aby2)
= x(x + ay) + by(x + ay)
= (x + ay) (x + by)

Example 8:    Factorize the following expression x2y2 – xy – 72
Solution:
In order to factorize x2y2 – xy – 72, we have to find two numbers p and q such that
p+ q = – 1 and pq = – 72
clearly, – 9 +8 = – 1 and – 9 × 8 = – 72.
So, we write the middle term – xy of
x2y2 – xy – 72 as – 9 xy + 8 xy, so that
x2y2 – xy – 72 = x2y2 – 9 xy + 8 xy – 72
= (x2y22 – 9xy) + (8xy – 72)
= xy (xy – 9) + 8 (xy – 9)
= (xy – 9) (xy + 8)

Factorization Of Polynomials Of The Form ax2 + bx + c, a ≠ 0, 1

Type I: Factorization of quadratic polynomials of the form ax2 + bx + c, a 0, 1
(i) In order to factorize ax2 + bx + c. We find numbers l and m such that l + m = b and lm = ac
(ii) After finding l and m, we split the middle term bx as lx + mx and get the desired factors by grouping the terms.

Example 9:    Factorize the following expression
6x2 – 5 x – 6
Solution:    The given expression is of the form ax2+ bx+c, where, a = 6, b = – 5 and c = –6.
In order to factorize the given expression, we have to find two numbers l and m such that
l + m = b = i.e., l + m = – 5
and lm = ac i.e. lm = 6 × – 6 = – 36
i.e., we have to find two factors of – 36
such that their sum is – 5. Clearly,
– 9 + 4 = – 5 and – 9 × 4 = – 36
l = – 9 and m = 4
Now, we split the middle term – 5x of
x2 – 5x – 6 as – 9 x + 4x, so that
6x2 – 5x – 6 = 6x2–9x + 4x – 6
= (6x2 – 9x) + (4x – 6)
= 3x (2x – 3) + 2(2x – 3) = (2x – 3) (3x + 2)

Example 10:    Factorize each of the following expressions:
(i) √3 x2 + 11x + 6 √3
(ii) 4 √3 x2 + 5x – 2 √3
(iii) 7 √2 x2 – 10 x – 4 √2
Solution:   (i) The given quadratic expression is of the form ax2 + bx + c,
where a = √3, b = 11 and c = 6 √3.
In order to factorize it, we have to find two numbers l and m such that
How To Factorise A Polynomial By Splitting The Middle Term 3
How To Factorise A Polynomial By Splitting The Middle Term 4
How To Factorise A Polynomial By Splitting The Middle Term 5
How To Factorise A Polynomial By Splitting The Middle Term 6

Example 11:    Factorize the following by splitting the middle term
1/3 x2 – 2x – 9
Solution:    
How To Factorise A Polynomial By Splitting The Middle Term 7

Type II: Factorization of trinomial expressions which are not quadratic but can be factorized by splitting the middle term.

Example 12:    Factorize the following trinomial by splitting the middle term
8a3 – 2a2b – 15 ab2
Solution:    Here a3 × ab2 = (a2b)2 i.e., the product of the variables in first and last term is same as the square of the variables in the middle term. So, in order to factorize the given trinomial, we split the middle term
– 2a2b as – 12a2b + 10 a2b , so that
8a3 – 2a2b – 15 ab2
= 8a3 –12a2b +10 a2b–15 ab2
= 4a2(2a – 3b) + 5 ab (2a – 3b)
= (2a – 3b) (4a2 + 5ab)
= (2a – 3b) a (4a + 5b)
= a (2a – 3 b) (4a + 5b)

Type III : Factorization of trinomial expressions reducible to quadratic expressions.

Example 13:    Factorize each of the following expressions by splitting the middle term :
(i) 9(x – 2y)2– 4(x – 2y) – 13
(ii) 2(x + y)2 – 9(x + y) – 5
(iii) 8(a + 1)2 + 2(a + 1) (b + 2) – 15(b + 2)2
Solution:    (i) The given expression is 9(x – 2y)2 – 4(x – 2y) – 13.
Putting x – 2y = a, we get
9(x – 2y)2 – 4(x – 2y) – 13 = 9a2 – 4a – 13
Now, 9a2 – 4a – 13 = 9a2 – 13a + 9a – 13
= (9a2 – 13a) + (9a – 13)
= a(9a – 13) + (9a – 13)
= (a + 1) (9a – 13)
Replacing a by x – 2y on both sides, we get
9(x – 2y)2 – 4(x – 2y) – 13
= (x – 2y + 1) {9(x – 2y) – 13}
= (x – 2y + 1) (9x – 18y – 13)
(ii) The given expression is
2(x + y)2 – 9(x + y) – 5
Replacing x + y by a in the given expression, we have
2(x + y)2 – 9(x + y) – 5 = 2a2 – 9a – 5
Now, 2a2 – 9a – 5 = 2a2 – 10a + a – 5
= (2a2 – 10a) + (a – 5)
= 2a(a – 5) + (a – 5) = (a – 5) (2a + 1)
Replacing a by x + y on both sides, we get
2(x + y)2 – 9(x + y) – 5
= (x + y – 5) {2(x + y) + 1}
= (x + y – 5) (2x + 2y + 1).
(iii) The given trinomial is
8(a + 1)2 + 2(a + 1) (b + 2) – 15(b + 2)2
Putting a + 1 = x and b + 2 = y, we have
8(a + 1)2 + 2(a + 1) (b + 2) – 15(b + 2)2
= 8x2 + 2xy – 15y2
= 8x2 + 12xy – 10xy – 15y2
= 4x(2x + 3y) – 5y(2x + 3y)
= (2x + 3y) (4x – 5y)
Replacing x by a + 1 and y by b + 2, we get
8(a + 1)2 + 2(a + 1) (b + 2) – 15(b + 2)2
= {2(a + 1) + 3(b + 2)} {4(a + 1) – 5(b +2)}
= (2a + 3b + 8) (4a – 5b – 6)