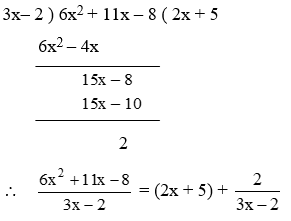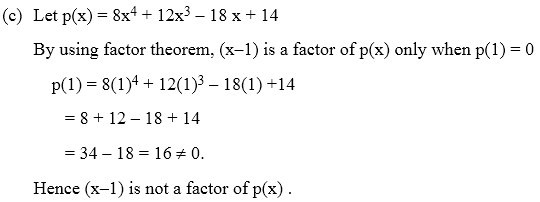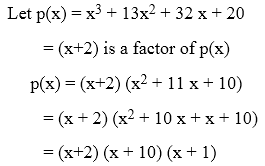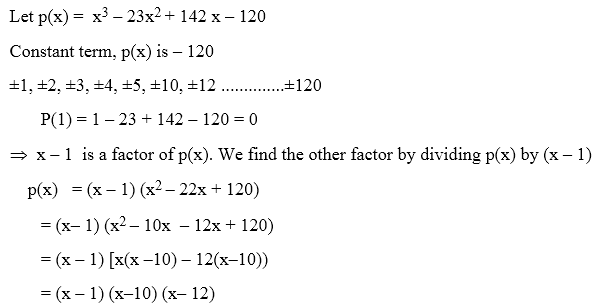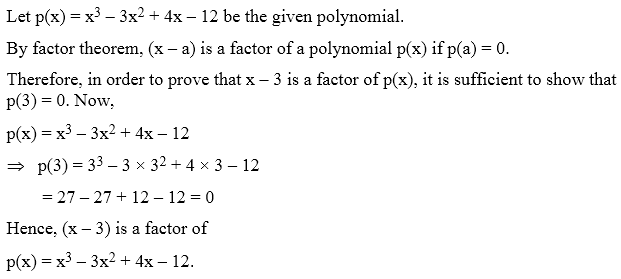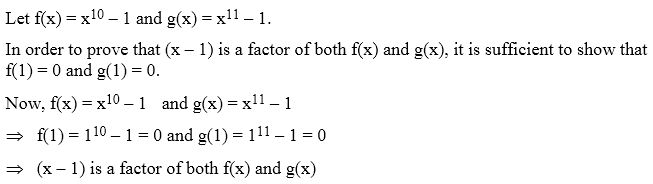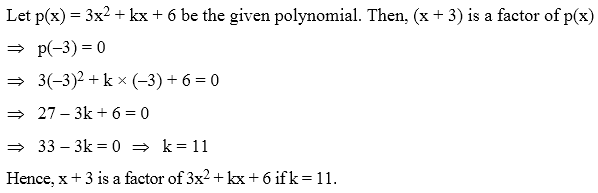Factor Theorem

Factorization Of Polynomials Using Factor Theorem

Factor Theorem:

If p(x) is a polynomial of degree n  1 and a is any real number, then (i) x – a is a factor of p(x), if p(a) = 0, and (ii) p(a) = 0, if x – a is a factor of p(x).
Proof: By the Remainder Theorem,
p(x) = (x – a) q(x) + p(a).
(i) If p(a) = 0, then p(x) = (x – a) q(x), which shows that x – a is a factor of p(x).
(ii) Since x – a is a factor of p(x),
p(x) = (x – a) g(x) for same polynomial g(x). In this case, p(a) = (a – a) g(a) = 0.

1. Obtain the polynomial p(x).
2. Obtain the constant term in p(x) and find its all possible factors. For example, in the polynomial
   x⁴ + x³ – 7x² – x + 6 the constant term is 6 and its factors are ± 1, ± 2, ± 3, ± 6.
3. Take one of the factors, say a and replace x by it in the given polynomial. If the polynomial reduces to zero, then (x – a) is a factor of polynomial.
4. Obtain the factors equal in no. to the degree of polynomial. Let these are (x–a), (x–b), (x–c.)…..
5. Write p(x) = k (x–a) (x–b) (x–c) ….. where k is constant.
6. Substitute any value of x other than a,b,c …… and find the value of k.

People also ask

• Division algorithm for polynomials
• Algebraic Identities Of Polynomials

Factorization Of Polynomials Using Factor Theorem Example Problems With Solutions

Example 1:    Factorize x² +4 + 9 z² + 4x – 6 xz – 12 z
Solution:
The presence of the three squares viz.x², (2)², and (3z)² gives a clue that identity (vii) could be used. So we write.
A = x² + (2)² + (3z)² + 4x – 6 xz – 12 z
We note that the last two of the product terms are negative and that both of these contain z. Hence we write A as
A = x² + (2)² + (–3z)² + 2.2x – 2.x.(–3z) + 2.2 (– 3z)
= (x+2 – 3z)²
= (x + 2 – 3z) (x + 2 – 3z)

Example 2:    Using factor theorem, factorize the polynomial x³ – 6x² + 11 x – 6.
Solution:
Let f(x) = x³ – 6x² + 11x – 6
The constant term in f(x) is equal to – 6 and factors of – 6 are ±1, ± 2, ± 3, ± 6.
Putting x = 1 in f(x), we have
f(1) = 1³ – 6 ×1² + 11× 1– 6
= 1 – 6 + 11– 6 = 0
∴ (x– 1) is a factor of f(x)
Similarly, x – 2 and x – 3 are factors of f(x).
Since f(x) is a polynomial of degree 3. So, it can not have more than three linear factors.
Let f(x) = k (x–1) (x– 2) (x – 3). Then,
x³– 6x² + 11x – 6 = k(x–1) (x– 2) (x– 3)
Putting x = 0 on both sides, we get
– 6 = k (0 – 1) (0 – 2) (0 – 3)
⇒ – 6 = – 6 k ⇒ k = 1
Putting k = 1 in f(x) = k (x– 1) (x– 2) (x–3), we get
f(x) = (x–1) (x– 2) (x – 3)
Hence, x³–6x² + 11x – 6 = (x– 1) (x – 2) (x–3)

Example 3:    Using factor theorem, factorize the polynomial x⁴ + x³ – 7x² – x + 6.
Solution:
Let f(x) = x⁴ + x³– 7x² –x + 6
the factors of constant term in f(x) are ±1, ±2, ±3 and ± 6
Now,

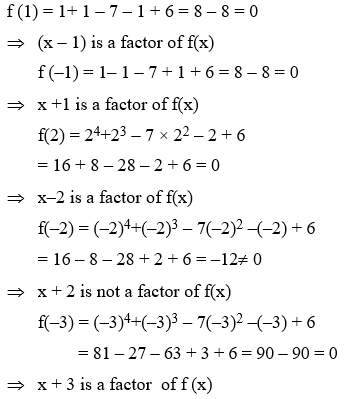
Since f(x) is a polynomial of degree 4. So, it cannot have more than 4 linear factors
Thus, the factors of f (x) are (x–1), (x+1),
(x–2) and (x+3).
Let f(x) = k (x–1) (x+1) (x–2) (x + 3)
⇒ x⁴ + x³ – 7x² – x + 6
= k (x–1) (x +1) (x – 2) (x + 3)
Putting x = 0 on both sides, we get
6 = k (–1) (1) (–2) (3) ⇒ 6 = 6 k ⇒ k = 1
Substituting k = 1 in (i), we get
x⁴ + x³ – 7x² – x + 6 = (x–1) (x +1) (x–2) (x+3)

Example 4:    Factorize,  2x⁴ + x³ – 14x² – 19x – 6
Solution:
Let f(x) = 2x⁴ + x³ – 14x² – 19x – 6 be the given polynomial. The factors of the constant term – 6 are ±1, ±2, ±3 and ±6, we have,
f(–1) = 2(–1)⁴ + (–1)³ – 14(–1)² – 19(–1)– 6
= 2 – 1 – 14 + 19 – 6 = 21 – 21 = 0
and,
f(–2) = 2(–2)⁴ + (–2)³ – 14(–2)² – 19(–2)– 6
= 32 – 8 – 56 + 38 – 6 = 0
So, x + 1 and x + 2 are factors of f(x).
⇒ (x + 1) (x + 2) is also a factor of f(x)
⇒ x² + 3x + 2 is a factor of f(x)
Now, we divide
f(x) = 2x⁴ +x³ – 14x²–19x – 6 by
x² + 3x + 2 to get the other factors.

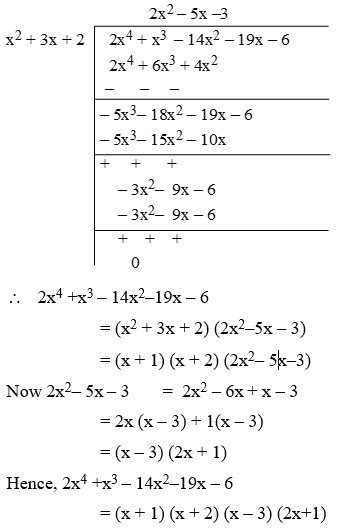
Example 5:    Factorize,  9z³ – 27z² – 100 z+ 300, if it is given that (3z+10) is a factor of it.
Solution:
Let us divide 9z³ – 27z² – 100 z+ 300 by
3z + 10 to get the other factors

∴ 9z³ – 27z² – 100 z+ 300
= (3z + 10) (3z²–19z + 30)
= (3z + 10) (3z²–10z – 9z + 30)
= (3z + 10) {(3z²–10z) – (9z – 30)}
= (3z + 10) {z(3z–10) – 3(3z–10)}
= (3z + 10) (3z–10) (z–3)
Hence, 9z³–27z²–100z+ 300
= (3z + 10) (3z–10) (z–3)

Example 6:    Simplify
\(\frac{4x-2}{{{x}^{2}}-x-2}+\frac{3}{2{{x}^{2}}-7x+6}-\frac{8x+3}{2{{x}^{2}}-x-3}\)
Solution:

Example 7:    Establish the identity
\(\frac{6{{x}^{2}}+11x-8}{3x-2}=\left( 2x+5 \right)+\frac{2}{3x-2}\)
Solution: