Exterior Angles of Triangle
Theorem: An measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
(non-adjacent interior angles may also be referred to as remote interior angles)
An exterior angle is formed by one side of a triangle and the extension of an adjacent side of the triangle.
In the triangle at the right, ∠4 is an exterior angle.
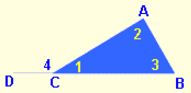 The theorem above states that if ∠4 is an exterior angle, its measure is equal to the sum of the measures of the 2 interior angles to which it is not adjacent, namely, ∠2 and ∠3.
The theorem above states that if ∠4 is an exterior angle, its measure is equal to the sum of the measures of the 2 interior angles to which it is not adjacent, namely, ∠2 and ∠3.
m∠4 = m∠2 + m∠3
Since the measure of an exterior angle equals the sum of its two non-adjacent interior angles, the exterior angle is also greater than either of the individual non-adjacent interior angles.
m∠4 > m∠2 and also m∠4 > m∠3
Theorem: The measure of an exterior angle of a triangle is greater than either of its two non-adjacent interior angles.
Examples
1. In ∆PQR, m∠Q = 45°, and m∠R = 72°. Find the measure of an exterior angle at P.
It is always helpful to draw a diagram and label it with the given information.
Then, using the first theorem above, set the exterior angle ( x ) equal to the sum of the two non-adjacent interior angles which are 45° and 72°.
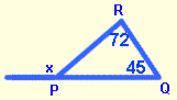
x = 45 + 72
x = 117
So, an exterior angle at P measures 117°.
2. In ∆DEF, an exterior angle at F is represented by 8x + 15. If the two non-adjacent interior angles are represented by 4x + 5, and 3x + 20, find the value of x.
First, draw and label a diagram.
Next, use the first theorem to set up an equation.
Then solve the equation for x.

8x + 15=(4x + 5)+(3x + 20)
8x + 15 = 7x + 25
8x = 7x + 10
x = 10
So, x = 10
3. Find the measure of an exterior angle at the base of an isosceles triangle whose vertex angle measures 40°.
First, draw and label a diagram.
You may choose to place the exterior angle at either vertex B or C. They will have the same measure.
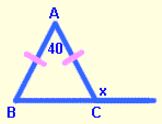
Next, we have to find the measure of a base angle–
— let’s say ∠B.
Remember that the 2 base angles of an isosceles triangle are equal, so we’ll represent each as y.
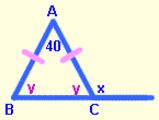
Then, write an equation, using the fact that there are 180 degrees in a triangle.
Now we can solve for x using the exterior angle theorem. Set the measure of the exterior angle equal to the sum of the measures of the two non-adjacent interior angles.
y + y + 40 = 180
2y + 40 = 180
2y = 140
y = 70
x = 70 + 40
x = 110
So, an exterior angle at the base measures 110°.