What is Hyperbolic Function?
Hyperbolic functions
We know that parametric co-ordinates of any point on the unit circle x2 + y2 = 1 is (cos θ, sin θ); so that these functions are called circular functions and co-ordinates of any point on unit hyperbola is
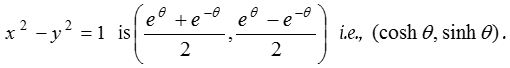
It means that the relation which exists amongst cos θ, sin θ and unit circle, that relation also exist amongst cosh θ, sinh θ and unit hyperbola. Because of this reason these functions are called as Hyperbolic functions.
For any (real or complex) variable quantity x,

Domain and range of hyperbolic functions
Let x is any real number
| Function | Domain | Range |
| sinh x | R | R |
| cosh x | R | [1, ∞) |
| tanh x | R | (–1, 1) |
| coth x | R0 | R – [–1, 1] |
| sech x | R | (0, 1] |
| cosech x | R0 | R0 |
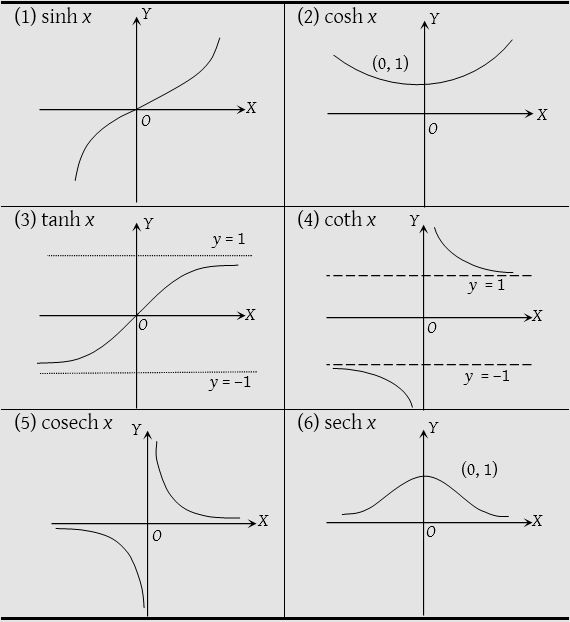
Graph of real hyperbolic functions
Formulae for hyperbolic functions
The following formulae can easily be established directly from above definitions
(1) Reciprocal formulae
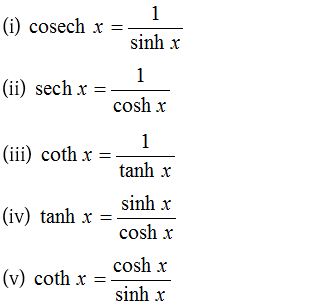
(2) Square formulae
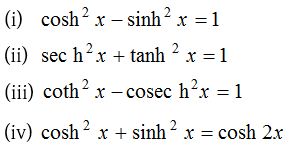
(3) Sum and difference formulae
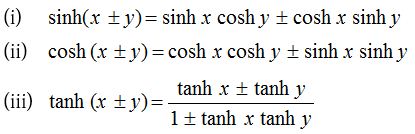
(4) Formulae to transform the product into sum or difference
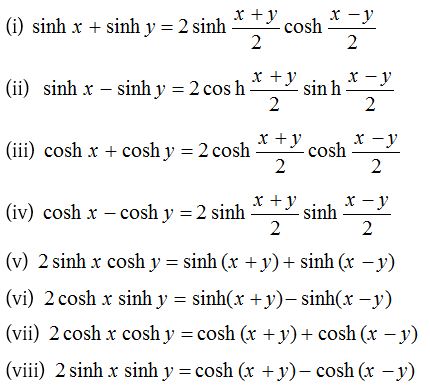
(5) Trigonometric ratio of multiple of an angle
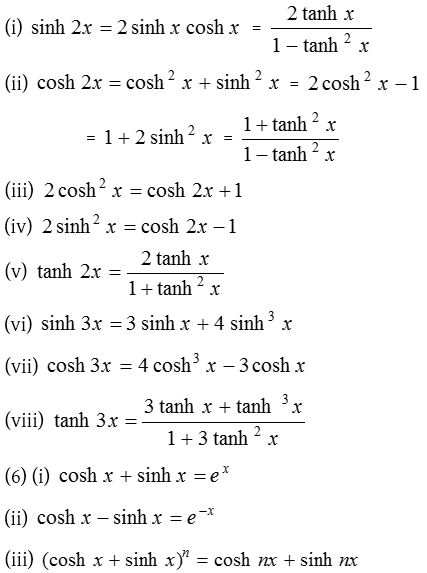
Transformation of a hyperbolic functions
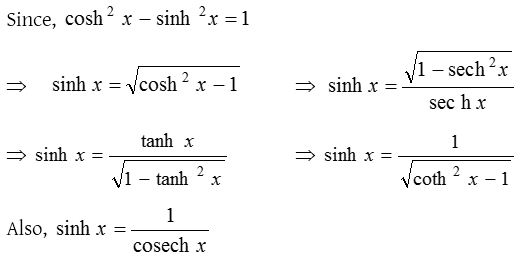
In a similar manner we can express cosh x, tanh x, coth x, ……………. in terms of other hyperbolic functions.
Expansion of hyperbolic functions
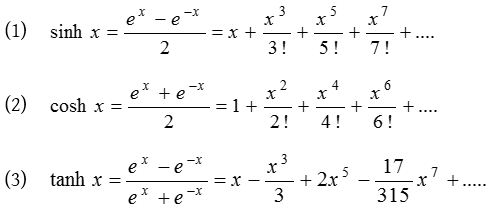
The expansion of coth x, cosech x does not exist because coth(0) = ∞ and cosech(0) = ∞.
Relation between hyperbolic, circular functions

Thus, we obtain the following relations between hyperbolic and trigonometrical functions.
| (1) | sin(ix) = i sinh x | (2) | cos(ix) = cosh x |
| sinh (ix) = i sin x | cosh (ix) = cos x | ||
| sinh x = −i sin (ix) | cosh x = cos (ix) | ||
| sin x = −i sinh (ix) | cos x = cosh (ix) | ||
| (3) | tan(ix) = i tanh x | (4) | cot(ix) = −i coth x |
| tanh (ix) = i tan x | coth (ix) = −i cot x | ||
| tanh x = −i tan(ix) | coth x = i cot(ix) | ||
| tan x = −i tanh (ix) | cot x = i coth (ix) | ||
| (5) | sec(ix) = sech x | (6) | cosec(ix) = −i cosech x |
| sech (ix) = sec x | cosech (ix) = −i cosec x | ||
| sech x = sec (ix) | cosech x = i cosec (ix) | ||
| sec x = sech (ix) | cosec x = i cosech (ix) |
Period of hyperbolic functions
If for any function f(x), f(x +T) = f(x), then f(x) is called the Periodic function and least positive value of T is called the Period of the function.
∵ sinh x = sinh(2πi + x); cosh x = cosh(2πi + x) and tanh x = tanh(πi + x)
Therefore the period of these functions are respectively 2πi, 2πi and πi. Also period of cosech x, sech x and coth x are respectively 2πi, 2πi and πi.
- Remember that if the period of f(x) is T, then period of f(nx) will be (T/n).
- Hyperbolic function are neither periodic functions nor their curves are periodic but they show the algebraic properties of periodic functions and having imaginary period.
Inverse hyperbolic functions
If sinh y = x, then y is called the inverse hyperbolic sine of x and it is written as y = sinh−1 x. Similarly cosech−1 x, cosh−1 x, tanh−1 x etc. can be defined.
(1) Domain and range of Inverse hyperbolic function
| Function | Domain | Range |
| sinh−1 x | R | R |
| cosh−1 x | [1, ∞) | R |
| tanh−1 x | (–1, 1) | R |
| coth−1 x | R – [–1, 1] | R0 |
| sech−1 x | (0, 1] | R |
| cosech−1 x | R0 | R0 |
(2) Relation between inverse hyperbolic function and inverse circular function
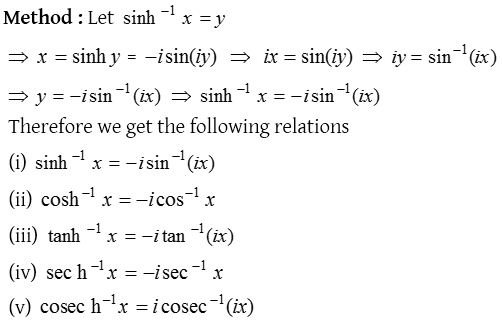
(3) To express any one inverse hyperbolic function in terms of the other inverse hyperbolic functions
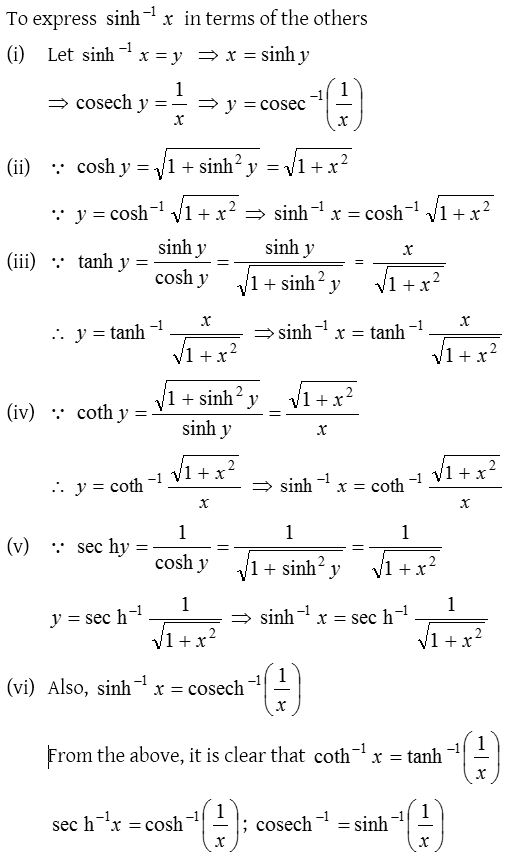
If x is real then all the above six inverse functions are single valued.
(4) Relation between inverse hyperbolic functions and logarithmic functions
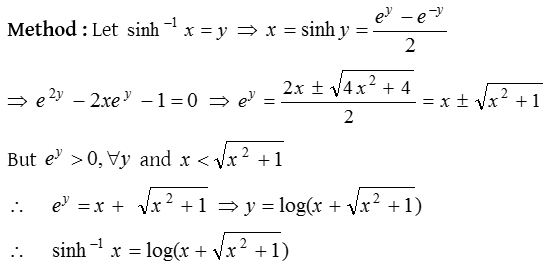
By the above method we can obtain the following relations between inverse hyperbolic functions and principal values of logarithmic functions.
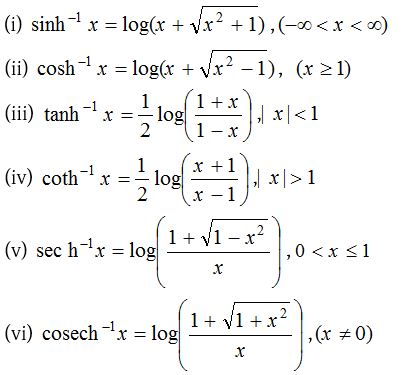
Formulae for values of cosech−1 x, sech−1 x, and coth−1 x may be obtained by replacing x by 1/x in the values of sinh−1 x, cosh−1 x and tanh−1 x respectively.
Separation of inverse trigonometric and inverse hyperbolic functions
If sin(α + iβ) = x + iy then (α + iβ), is called the inverse sine of (x + iy). We can write it as, sin−1(x + iy) = α + iβ.
Here the following results for inverse functions may be easily established.
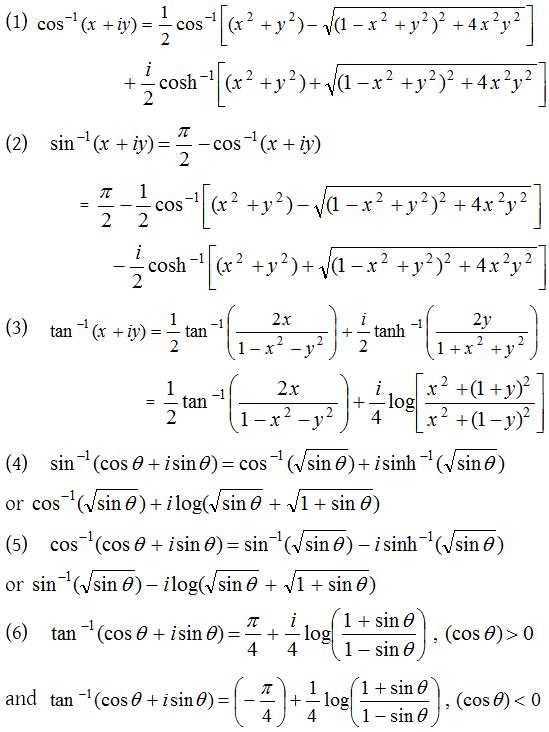
Since each inverse hyperbolic function can be expressed in terms of logarithmic function, therefore for separation into real and imaginary parts of inverse hyperbolic function of complex quantities use the appropriate method.
Both inverse circular and inverse hyperbolic functions are many valued.