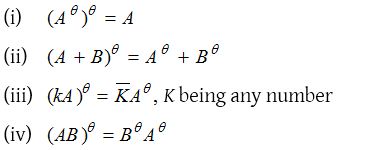What are the Special Types of Matrices?

What are the Special Types of Matrices?

Singular and Non-singular matrix :

Any square matrix A is said to be non-singular if |A| ≠ 0, and a square matrix A is said to be singular if |A| = 0. Here |A| (or det(A) or simply det |A| means corresponding determinant of square matrix A.

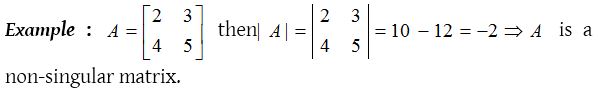
Hermitian and Skew-hermitian matrix :

A square matrix is said to be hermitian matrix if

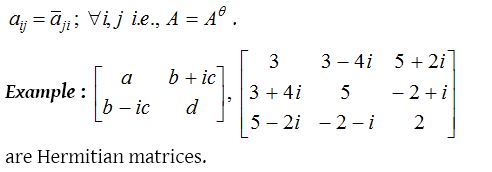
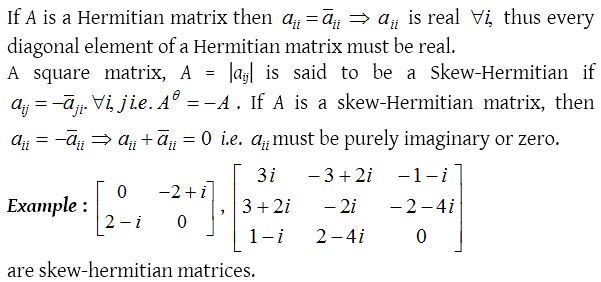
Orthogonal matrix :

A square matrix A is called orthogonal if AA^T = I = A^T A i.e., if A⁻¹ = A.

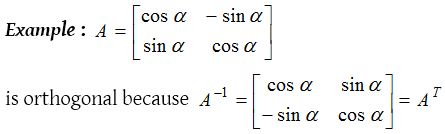
In fact every unit matrix is orthogonal. Determinant of orthonogal matrix is – 1 or 1.

Idempotent matrix :

A square matrix A is called an idempotent matrix if A² = A.

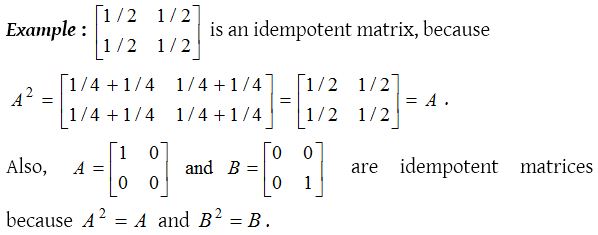
In fact every unit matrix is indempotent.

Involutory matrix :

A square matrix A is called an involutory matrix if A² = I or A⁻¹ = A.

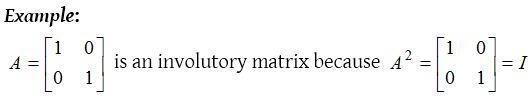
In fact every unit matrix is involutory.

Nilpotent matrix :

A square matrix A is called a nilpotent matrix if there exists a p ∈ N such that A^p = 0.

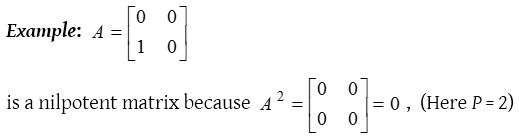
Determinant of every nilpotent matrix is 0.

Periodic matrix :

A matrix A will be called a periodic matrix if where k is a positive integer. If A^k+1 = A however k is the least positive integer for A^k+1 = A, then k is said to be the period of A.
Differentiation of a matrix : If then is a differentiation of matrix A.

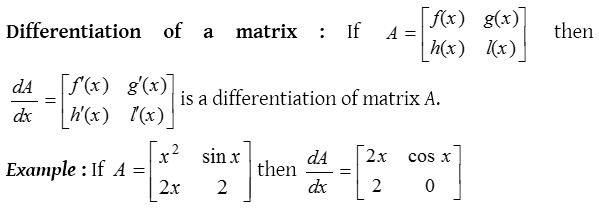
Conjugate of a matrix :

The matrix obtained from any given matrix A containing complex number as its elements, on replacing its elements by the corresponding conjugate complex numbers is called conjugate of A and is denoted by \(\overline { A }\).

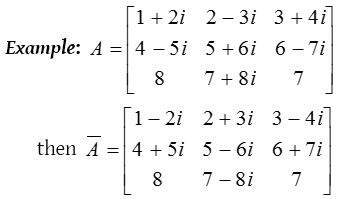
Properties of conjugates

Transpose conjugate of a matrix :

The transpose of the conjugate of a matrix A is called transposed conjugate of A and is denoted by A^θ. The conjugate of the transpose of A is the same as the transpose of the conjugate of A

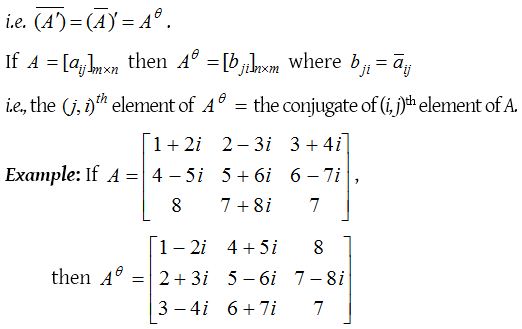
Properties of transpose conjugate