RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables

RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables

Exercise 3A

Question 1:



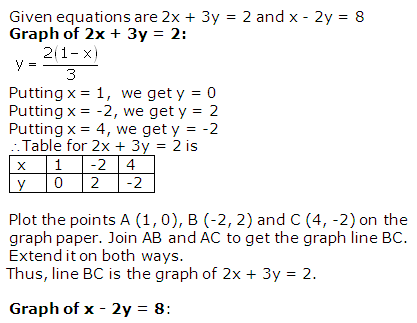
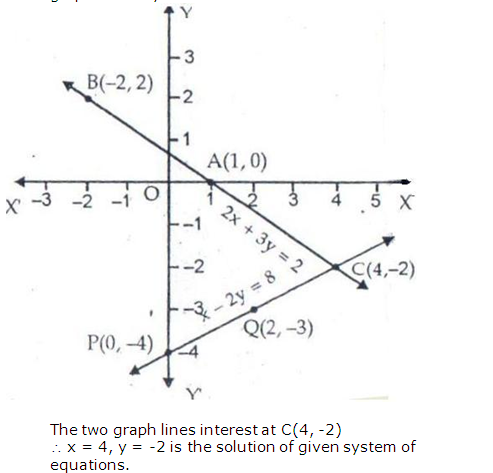h3

Read More:

• What is a Linear Equation
• Linear Equations In One Variable
• Linear Equations In Two Variables
• Graphical Method Of Solving Linear Equations In Two Variables

Question 2:

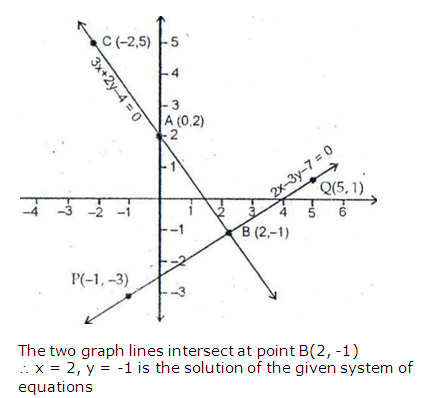
More Resources

• RS Aggarwal Solutions Class 10
• RD Sharma Class 10 Solutions
• NCERT Solutions

Question 3:


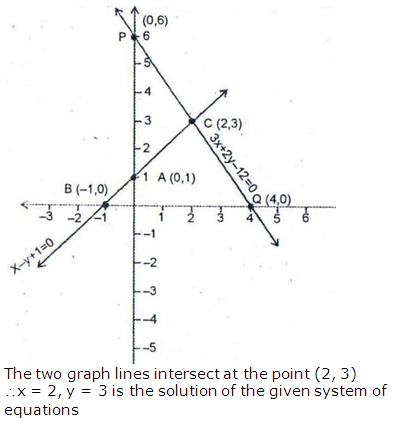
Question 4:


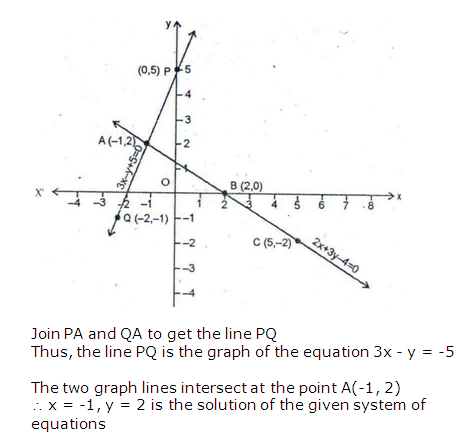
Question 5:


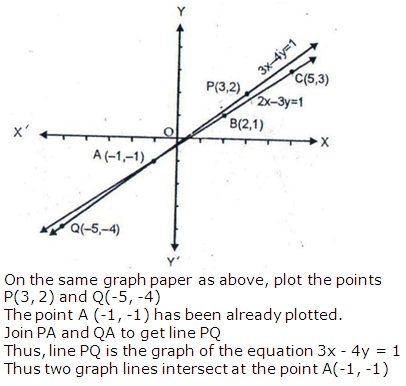
Question 6:


Question 7:


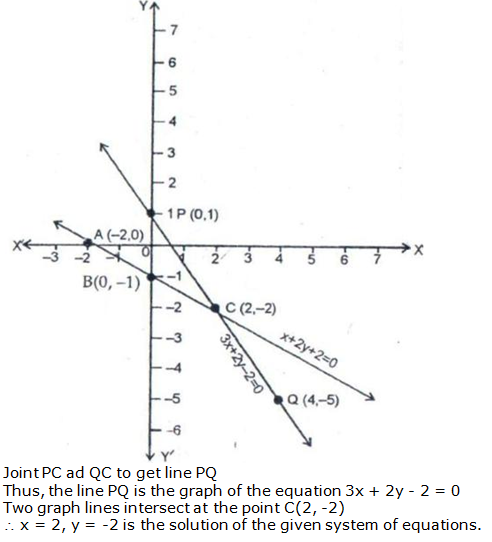
Question 8:


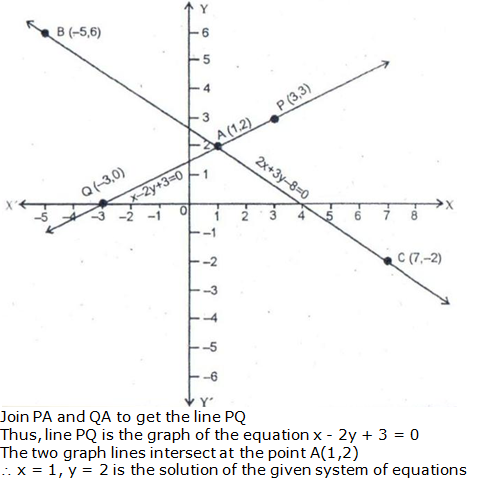
Question 9:


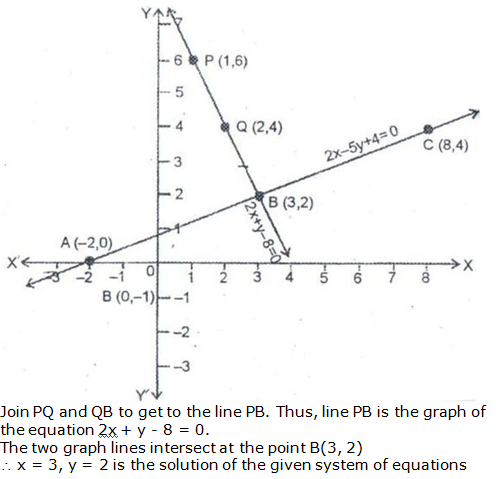
Question 10:


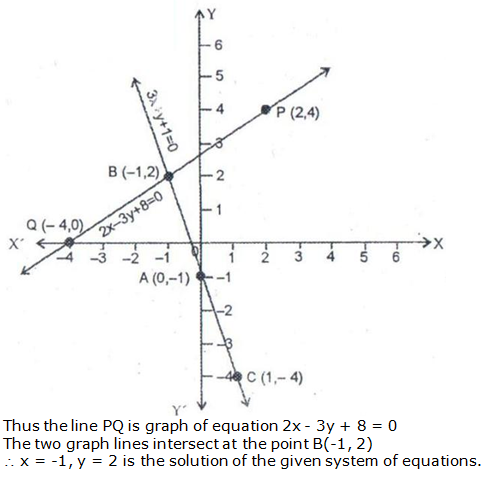
Question 11:


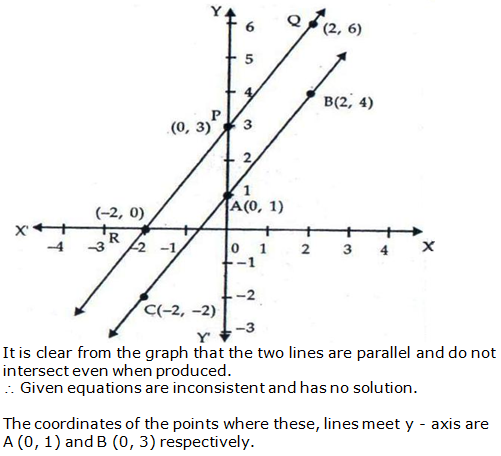
Question 12:


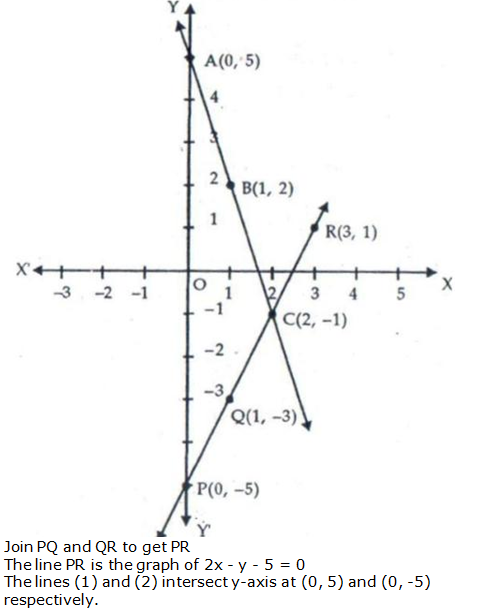
Question 13:


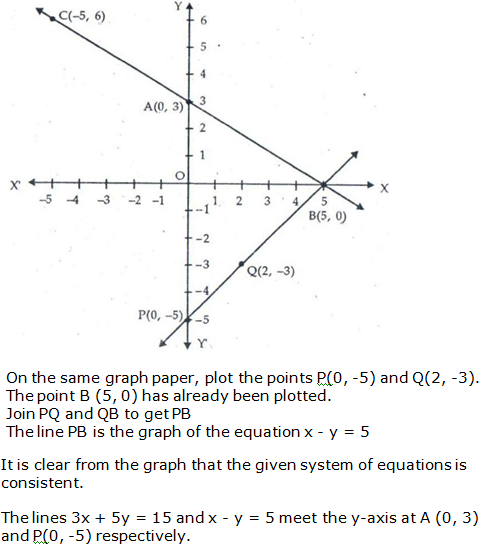
Question 14:


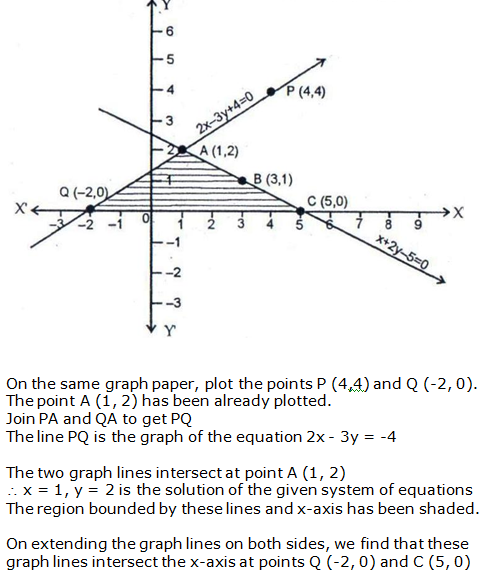
Question 15:


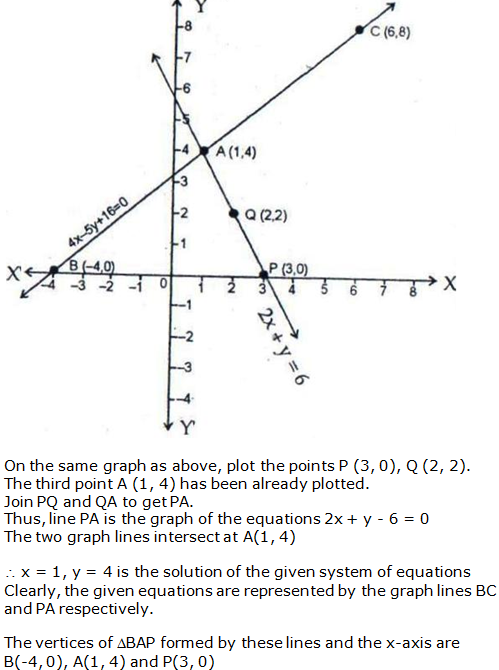
Question 16:


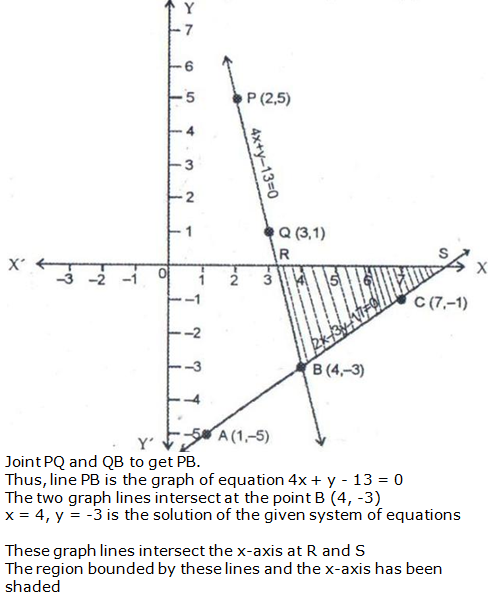
Question 17:


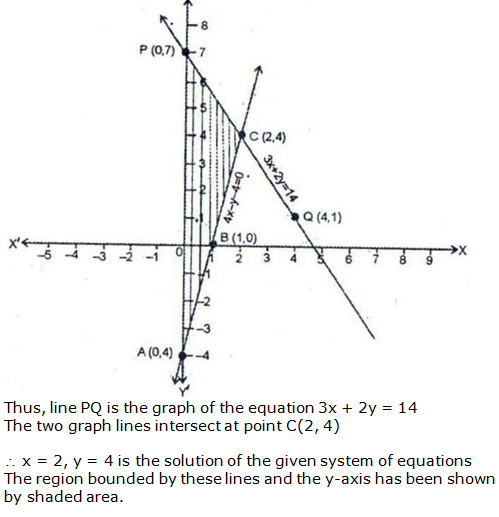
Question 18:


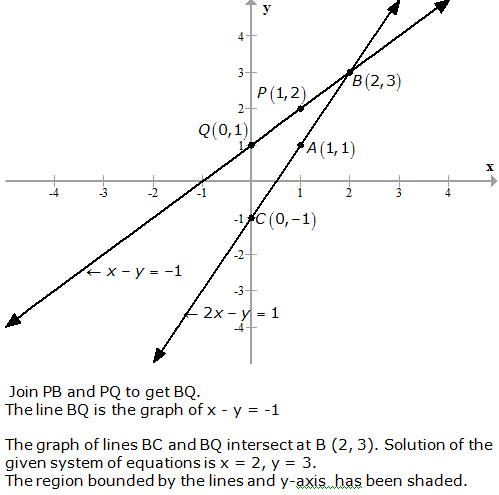
Question 19:

Question 20:


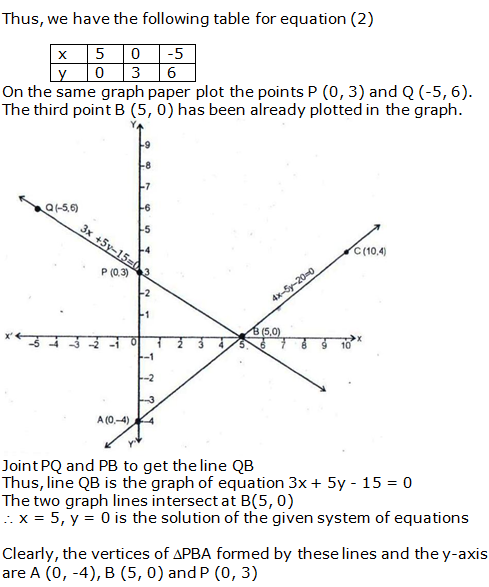
Question 21:


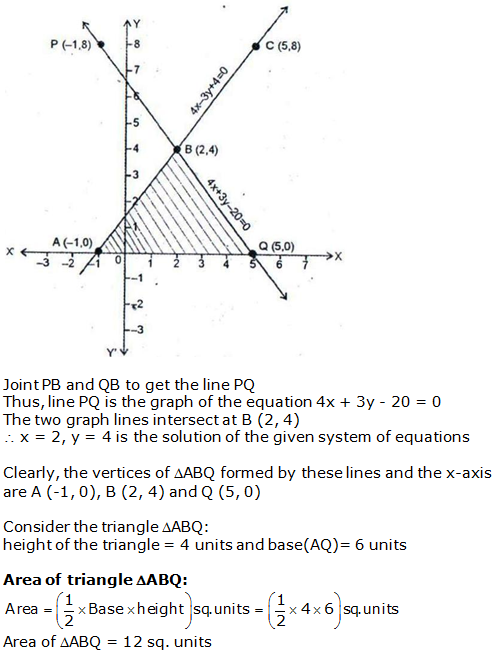
Question 22:


Question 23:



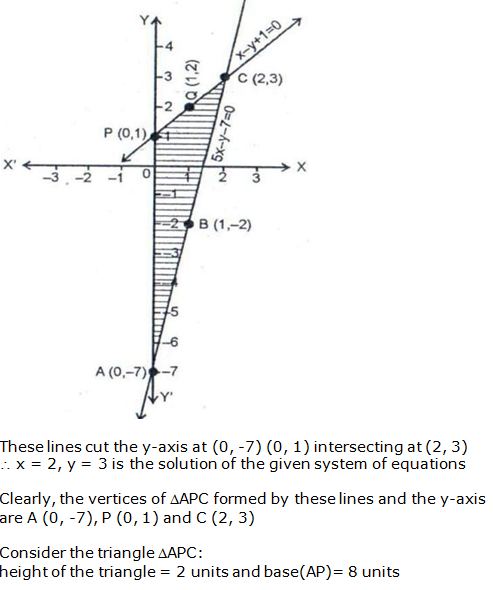
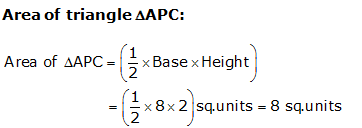
Question 24:


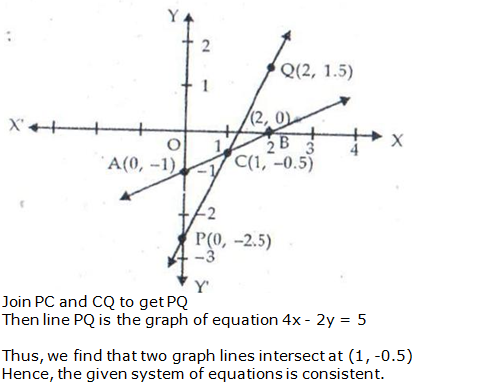
Question 25:


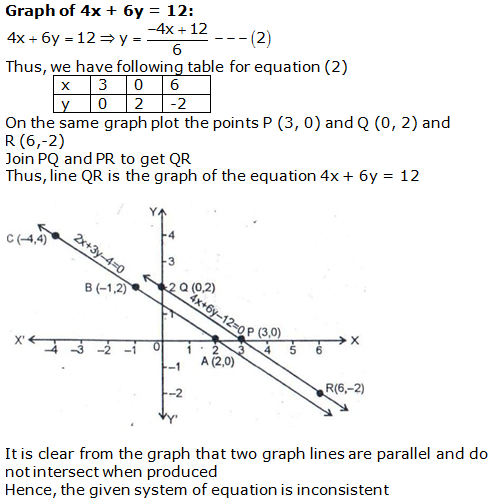
Question 26:


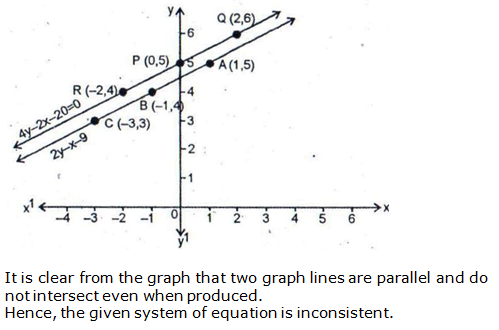
Question 27:



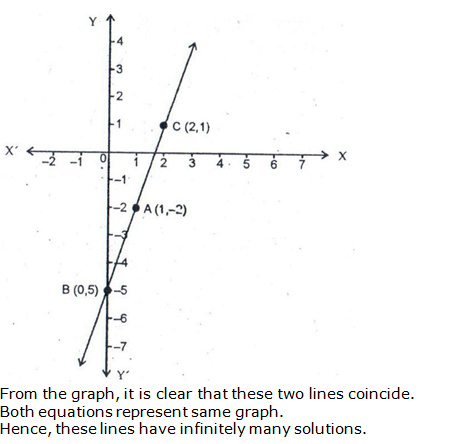
Question 28:

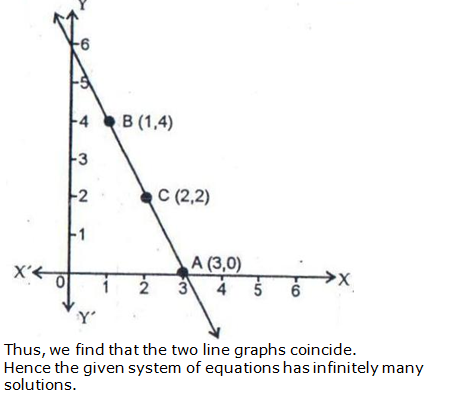
Exercise 3B

Question 1:

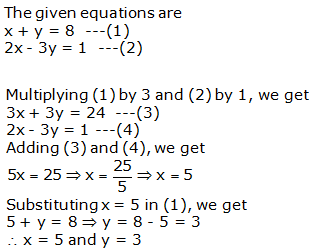
Question 2:

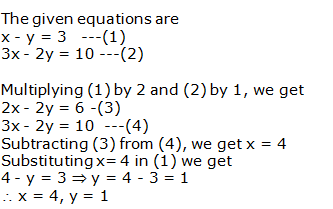
Question 3:

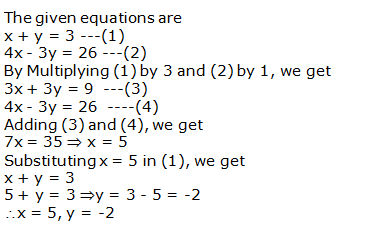
Question 4:

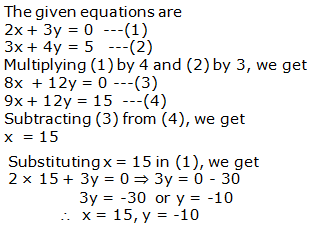
Question 5:

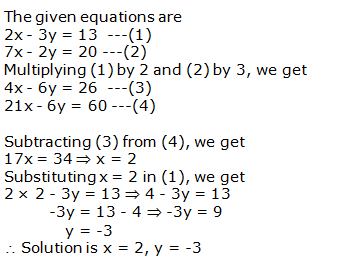
Question 6:

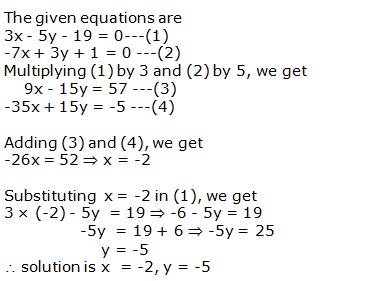
Question 7:

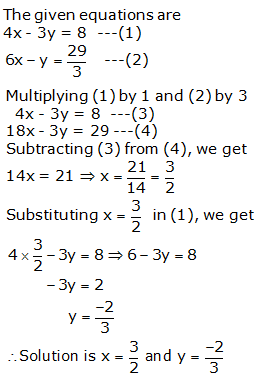
Question 8:

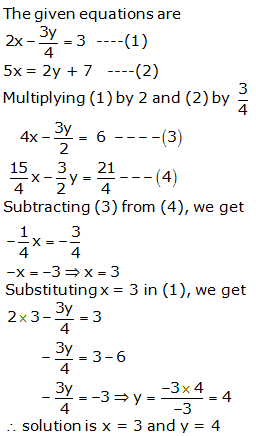
Question 9:

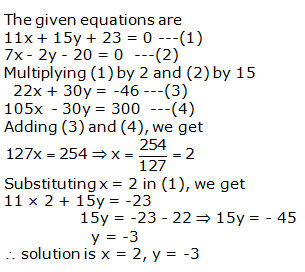
Question 10:

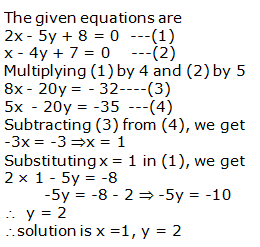
Question 11:

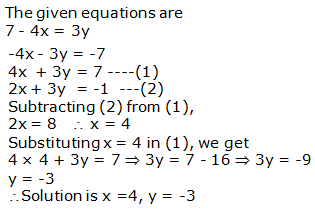
Question 12:

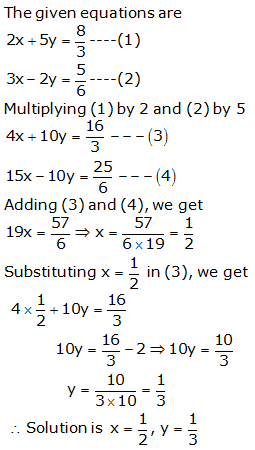
Question 13:

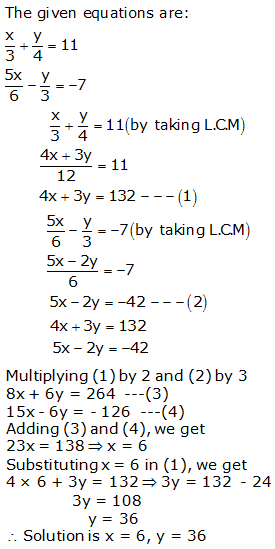
Question 14:

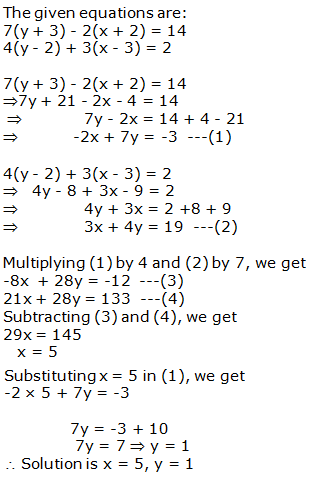
Question 15:

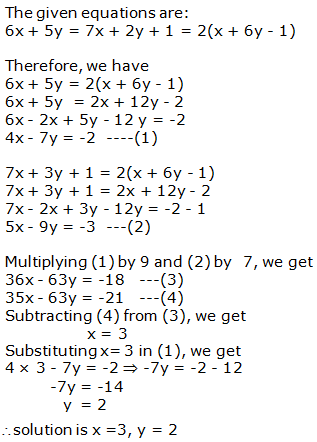
Question 16:

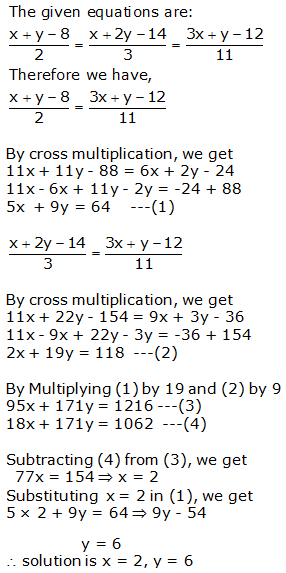
Question 17:

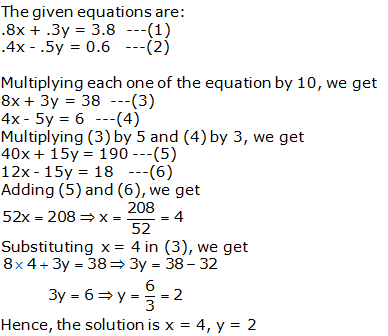
Question 18:

Question 19:

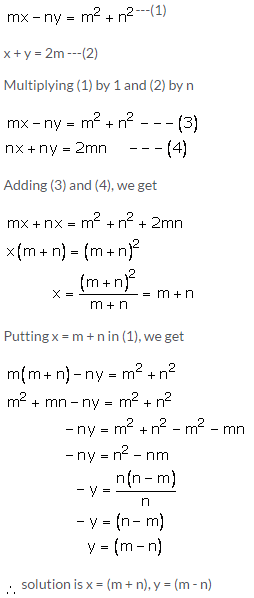
Question 20:

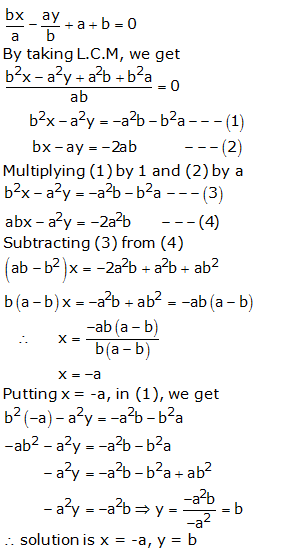
Question 21:

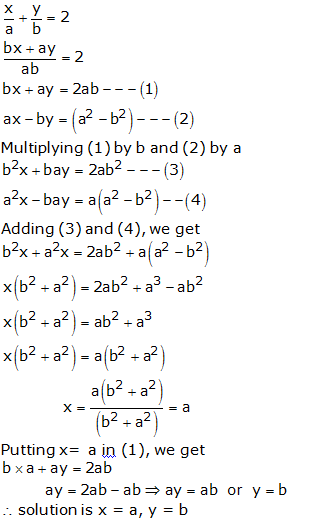
Question 22:

Taking L.C.M, we get

Multiplying (1) by 1 and (2) by

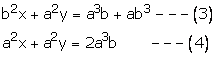
Subtracting (4) from (3), we get

Substituting x = ab in (3), we get

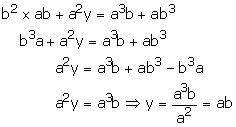
Therefore solution is x = ab, y = ab
Question 23:
6(ax + by) = 3a + 2b
6ax + 6by = 3a + 2b —(1)
6(bx – ay) = 3b – 2a
6bx – 6ay = 3b- 2a —(2)
6ax + 6by = 3a + 2b —(1)
6bx – 6ay = 3b – 2a —(2)
Multiplying (1) by a and (2) by b

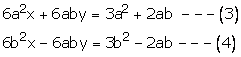
Adding (3) and (4), we get

Substituting in (1), we get

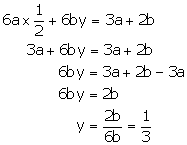
Hence, the solution is

Question 24:

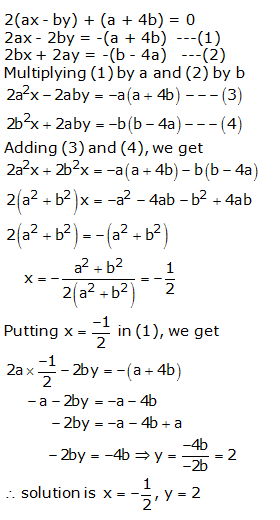
Question 25:
The given equations are
71x + 37y = 253 —(1)
37x + 71y = 287 —(2)
Adding (1) and (2)
108x + 108y = 540
108(x + y) = 540
—-(3)
Subtracting (2) from (1)
34x – 34y = 253 – 287 = -34
34(x – y) = -34
—(4)
Adding (3) and (4)
2x = 5 – 1= 4
⇒ x = 2
Subtracting (4) from (3)
2y = 5 + 1 = 6
⇒ y = 3
Hence solution is x = 2, y = 3
Question 26:
37x + 43y = 123 —-(1)
43x + 37y = 117 —-(2)
Adding (1) and (2)
80x + 80y = 240
80(x + y) = 240
x + y = —-(3)
Subtracting (1) from (2),
6x – 6y = -6
6(x – y) = -6
—-(4)
Adding (3) and (4)
2x = 3 – 1 = 2
⇒ x = 1
Subtracting (4) from (3),
2y = 3 + 1 = 4
⇒ y = 2
Hence solution is x = 1, y = 2
Question 27:
217x + 131y = 913 —(1)
131x + 217y = 827 —(2)
Adding (1) and (2), we get
348x + 348y = 1740
348(x + y) = 1740
x + y = 5 —-(3)
Subtracting (2) from (1), we get
86x – 86y = 86
86(x – y) = 86
x – y = 1 —(4)
Adding (3) and (4), we get
2x = 6
x = 3
putting x = 3 in (3), we get
3 + y = 5
y = 5 – 3 = 2
Hence solution is x = 3, y = 2
Question 28:
41x – 17y = 99 —(1)
17x – 41y = 75 —(2)
Adding (1) and (2), we get
58x – 58y = 174
58(x – y) = 174
x – y = 3 —(3)
subtracting (2) from (1), we get
24x + 24y = 24
24(x + y) = 24
x + y = 1 —(4)
Adding (3) and (4), we get
2x = 4 x = 2
Putting x = 2 in (3), we get
2 – y = 3
-y = 3 – 2 y = -1
Hence solution is x =2, y = -1

Exercise 3C

Question 1:
x + 2y + 1 = 0 —(1)
2x – 3y – 12 = 0 —(2)
By cross multiplication, we have

Hence, x = 3 and y = -2 is the solution
Question 2:
2x + 5y – 1 = 0 —(1)
2x + 3y – 3 = 0 —(2)
By cross multiplication we have

Hence the solution is x = 3, y = -1
Question 3:
3x – 2y + 3 = 0
4x + 3y – 47 = 0
By cross multiplication we have

Hence the solution is x = 5, y = 9
Question 4:
6x – 5y – 16 = 0
7x – 13y + 10 = 0
By cross multiplication we have

Hence the solution is x = 6, y = 4
Question 5:
3x + 2y + 25 = 0
2x + y + 10 = 0
By cross multiplication, we have

Hence the solution is x = 5, y = -20
Question 6:
2x + y – 35 = 0
3x + 4y – 65 = 0
By cross multiplication, we have

Question 7:
7x – 2y – 3 = 0
By cross multiplication, we have

Hence x = 1, y = 2 is the solution
Question 8:

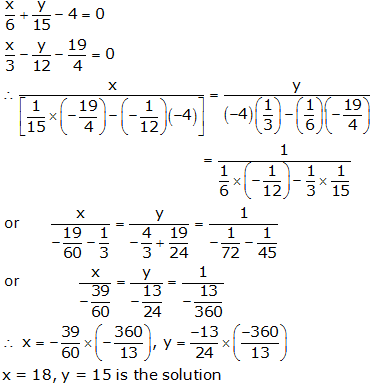
Question 9:
ax + by – (a – b) = 0
bx – ay – (a + b) = 0
By cross multiplication, we have

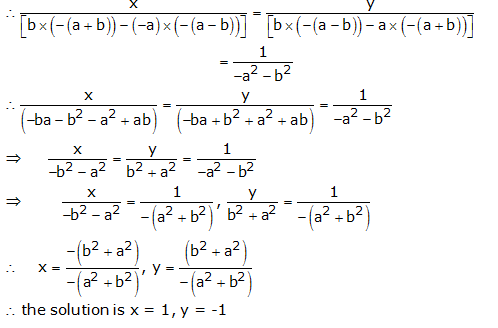
Question 10:
2ax + 3by – (a + 2b) = 0
3ax + 2by – (2a + b) = 0
By cross multiplication, we have

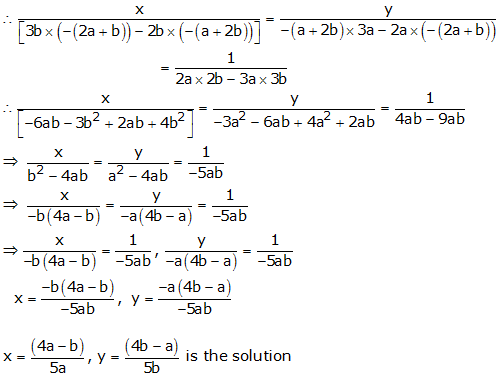
Question 11:

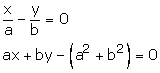
By cross multiplication, we have

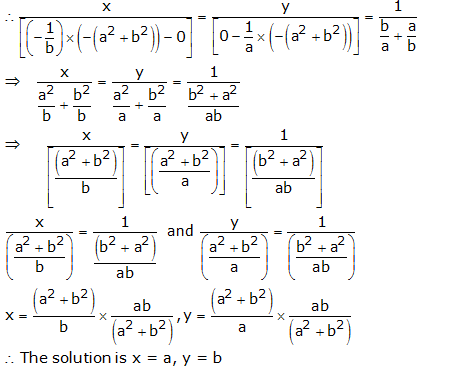
Question 12:

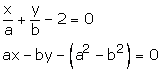
By cross multiplication, we have

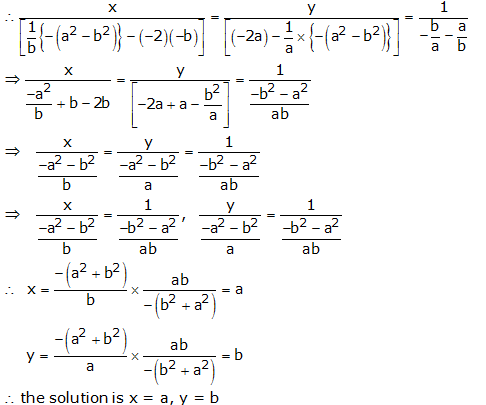
Question 13:

By cross multiplication we have

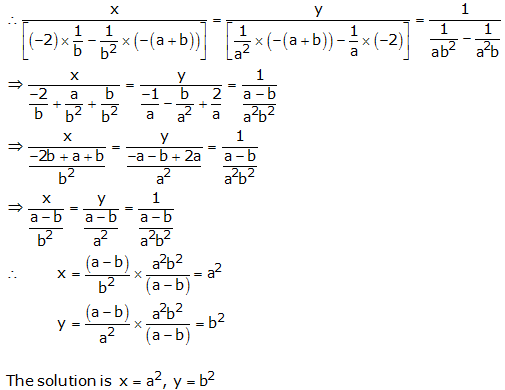
Question 14:

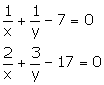
Taking

u + v – 7 = 0
2u + 3v – 17 = 0
By cross multiplication, we have

Hence the solution is

Question 15:
Let

in the equation
5u – 2v + 1 = 0
15u + 7v – 10 = 0

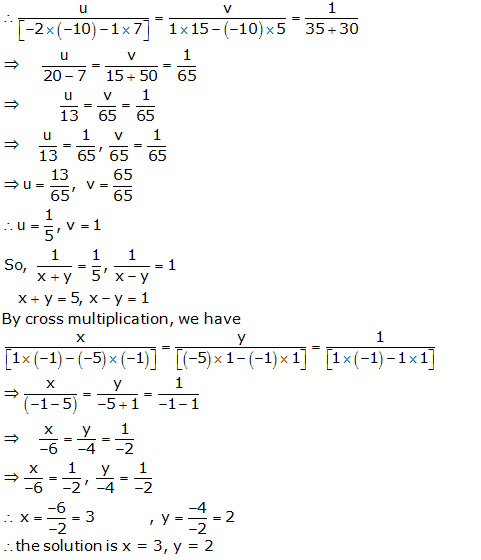
Question 16:

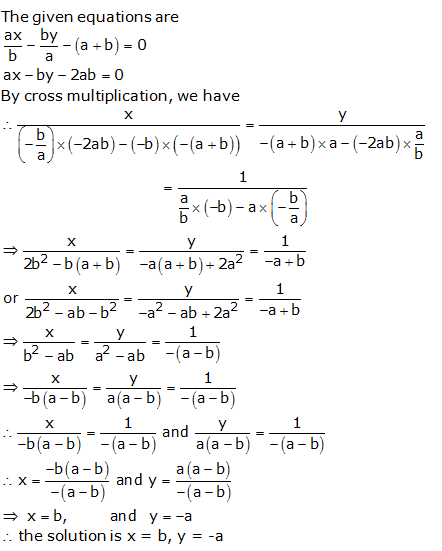
Exercise 3D

Question 1:

Question 2:

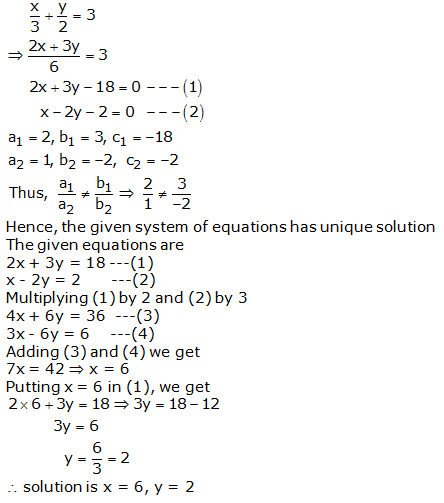
Question 3:
3x – 5y – 7 = 0
6x – 10y – 3 = 0

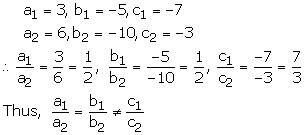
Hence the given system of equations is inconsistent
Question 4:
2x – 3y – 5 = 0, 6x – 9y – 15 = 0
These equations are of the form

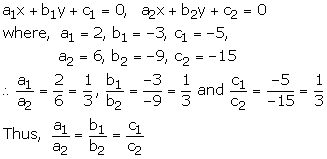
Hence the given system of equations has infinitely many solutions
Question 5:
kx + 2y – 5 = 0
3x – 4y – 10 = 0
These equations are of the form

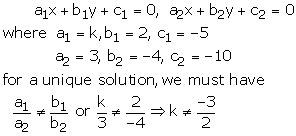
This happens when
\(k\neq \frac { -3 }{ 2 }\)
Thus, for all real value of k other that , the given system equations will have a unique solution
(ii) For no solution we must have


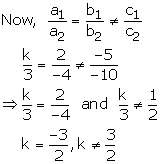
Hence, the given system of equations has no solution if \(k=\frac { -3 }{ 2 } \)
Question 6:
x + 2y – 5 = 0
3x + ky + 15 = 0
These equations are of the form of

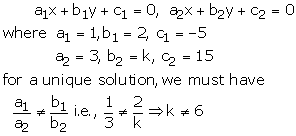
Thus for all real value of k other than 6, the given system of equation will have unique solution
(ii) For no solution we must have

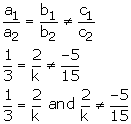
Therefore k = 6
Hence the given system will have no solution when k = 6.
Question 7:
x + 2y – 3 = 0, 5x + ky + 7 = 0
These equations are of the form

(i) For a unique solution we must have

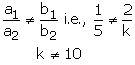
Thus, for all real value of k other than 10
The given system of equation will have a unique solution.
(ii) For no solution we must have

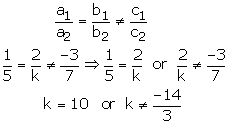
Hence the given system of equations has no solution if

For infinite number of solutions we must have

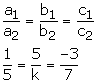
This is never possible since

There is no value of k for which system of equations has infinitely many solutions
Question 8:
8x + 5y – 9 = 0
kx + 10y – 15 = 0
These equations are of the form

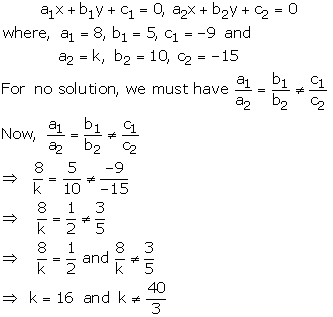
Clearly, k = 16 also satisfies the condition

Hence, the given system will have no solution when k = 16.
Question 9:
kx + 3y – 3 = 0 —-(1)
12x + ky – 6 = 0 —(2)

These equations are of the form

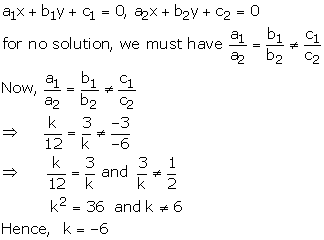
Hence, the given system will have no solution when k = -6
Question 10:
3x + y – 1 = 0
(2k – 1)x + (k – 1)y – (2k + 1) = 0
These equations are of the form

Thus,

Hence the given equation has no solution when k = 2
Question 11:
(3k + 1)x + 3y – 2 = 0
(k² + 1)x + (k – 2)y – 5 = 0
these equations are of the form

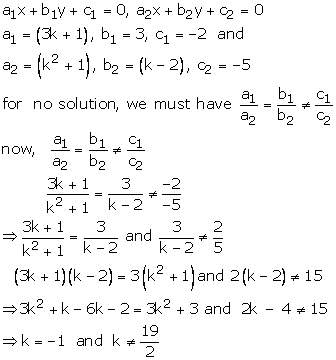
Thus, k = -1 also satisfy the condition

Hence, the given system will have no solution when k = -1
Question 12:
The given equations are
3x – y – 5 = 0 —(1)
6x – 2y + k = 0—(2)

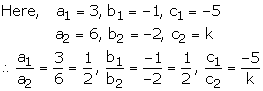
Equations (1) and (2) have no solution, if

Question 13:
kx + 2y – 5 = 0
3x + y – 1 = 0
These equations are of the form

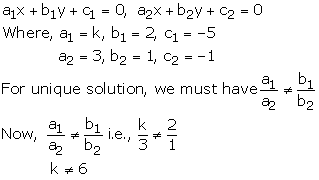
Thus, for all real values of k other than 6, the given system of equations will have a unique solution
Question 14:
x – 2y – 3 = 0
3x + ky – 1 = 0
These equations are of the form of

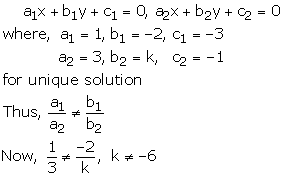
Thus, for all real value of k other than -6, the given system of equations will have a unique solution
Question 15:
kx + 3y – (k – 3) = 0
12x + ky – k = 0
These equations are of the form

Thus, for all real value of k other than , the given system of equations will have a unique solution
Question 16:
4x – 5y – k = 0, 2x – 3y – 12 = 0
These equations are of the form

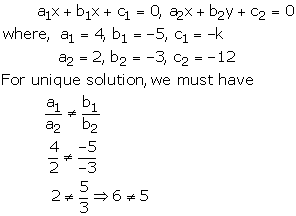
Thus, for all real value of k the given system of equations will have a unique solution
Question 17:
2x + 3y – 7 = 0
(k – 1)x + (k + 2)y – 3k = 0
These are of the form

This hold only when

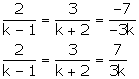
Now the following cases arises
Case : I

Case: II

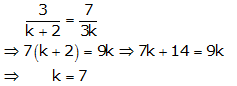
Case III

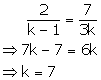
For k = 7, there are infinitely many solutions of the given system of equations
Question 18:
2x + (k – 2)y – k = 0
6x + (2k – 1)y – (2k + 5) = 0
These are of the form

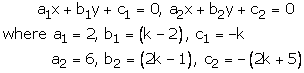
For infinite number of solutions, we have

This hold only when

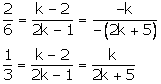
Case (1)

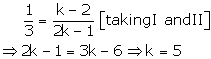
Case (2)

Case (3)

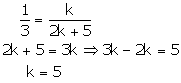
Thus, for k = 5 there are infinitely many solutions
Question 19:
kx + 3y – (2k +1) = 0
2(k + 1)x + 9y – (7k + 1) = 0
These are of the form

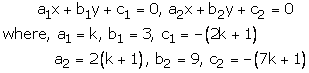
For infinitely many solutions, we must have

This hold only when

Now, the following cases arise
Case – (1)

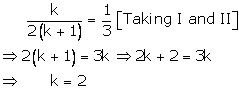
Case (2)

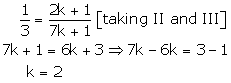
Case (3)


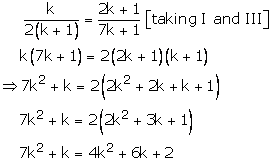
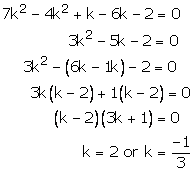
Thus, k = 2, is the common value for which there are infinitely many solutions
Question 20:
5x + 2y – 2k = 0
2(k +1)x + ky – (3k + 4) = 0
These are of the form

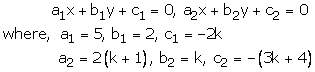
For infinitely many solutions, we must have

These hold only when

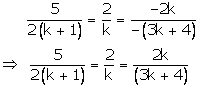
Case I



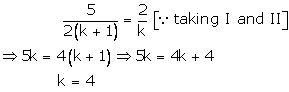
Thus, k = 4 is a common value for which there are infinitely by many solutions.
Question 21:
x + (k + 1)y – 5 = 0
(k + 1)x + 9y – (8k – 1) = 0
These are of the form

For infinitely many solutions, we must have

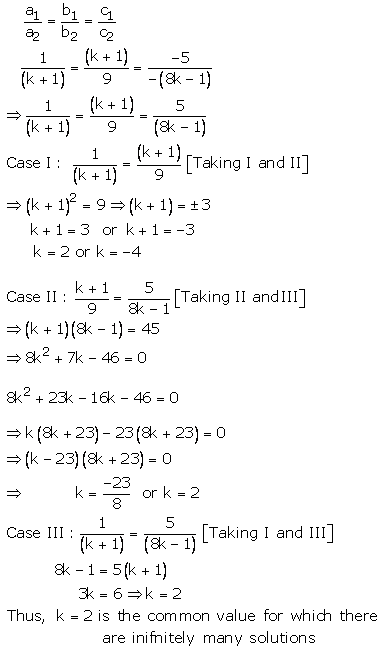
Question 22:
(k – 1)x – y – 5 = 0
(k + 1)x + (1 – k)y – (3k + 1) = 0
These are of the form

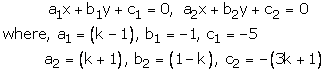
For infinitely many solution, we must now

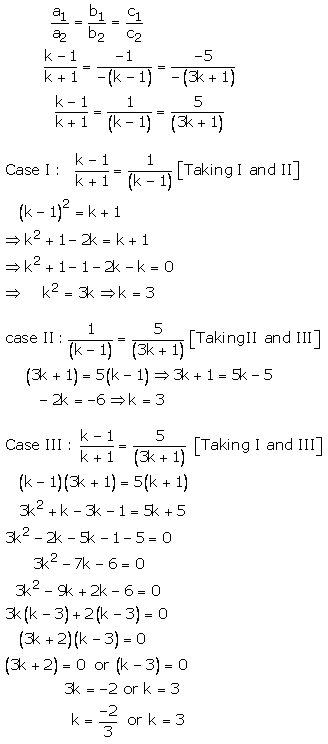
k = 3 is common value for which the number of solutions is infinitely many
Question 23:
(a – 1)x + 3y – 2 = 0
6x + (1 – 2b)y – 6 = 0
These equations are of the form

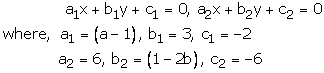
For infinite many solutions, we must have

Hence a = 3 and b = -4
Question 24:
(2a – 1)x + 3y – 5 = 0
3x + (b – 1)y – 2 = 0
These equations are of the form

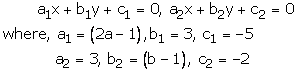
These holds only when

Question 25:
2x – 3y – 7 = 0
(a + b)x + (a + b – 3)y – (4a + b) = 0
These equation are of the form

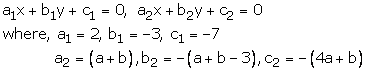
For infinite number of solution

Putting a = 5b in (2), we get

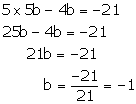
Putting b = -1 in (1), we get

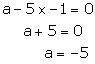
Thus, a = -5, b = -1
Question 27:
The given equations are
2x + 3y = 7 —-(1)
a(x + y) – b(x – y) = 3a + b – 2 —(2)
Equation (2) is
ax + ay – bx + by = 3a + b – 2
(a – b)x + (a + b)y = 3a + b -2
Comparing with the equations

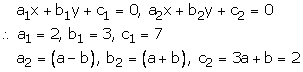
There are infinitely many solution

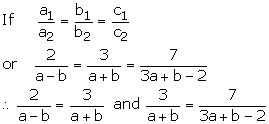
2a + 2b = 3a – 3b and 3(3a + b – 2) = 7(a + b)
-a = -5b and 9a + 3b – 6 = 7a + 7b
a = 5b and 9a – 7a + 3b – 7b = 6
or 2a – 4b = 6
or a – 2b = 3
thus equation in a, b are
a = 5b —(3)
a – 2b = 3 —(4)
putting a = 5b in (4)
5b – 2b = 3 or 3b = 3 Þ b = 1
Putting b = 1 in (3)
a = 5 and b = 1
Question 28:
We have 5x – 3y = 0 —(1)
2x + ky = 0 —(2)
Comparing the equation with

These equations have a non – zero solution if

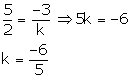
Exercise 3E

Question 1:
Let the cost of 1 chair be Rs x and the cost of one table be Rs. y
The cost of 5 chairs and 4 tables = Rs(5x + 4y) = Rs. 2800
5x + 4y = 2800 —(1)
The cost of 4 chairs and 3 tables = Rs(4x + 3y) = Rs. 2170
4x + 3y = 2170 —(2)
Multiplying (1) by 3 and (2) by 4, we get
15x + 12y = 8400 —(3)
16x + 12y = 8680 —(4)
Subtracting (3) and (4), we get
x = 280
Putting value of x in (1), we get
5 × 280 + 4y = 2800
or 1400 + 4y = 2800
or 4y = 1400
\(y=\frac { 1400 }{ 4 } =350 \)
Thus, cost of 1 chair = Rs. 280 and cost of 1 table = Rs. 350
Question 2:
Let the cost of a pen and a pencil be Rs x and Rs y respectively
Cost of 37 pens and 53 pencils = Rs(37x + 53y) = Rs 820
37x + 53y = 820 —(1)
Cost of 53 pens and 37 pencils = Rs(53x + 37y) = Rs 980
53x + 37y = 980 —(2)
Adding (1) and (2), we get
90x + 90y = 1800
x + y = 20 —(3)
y = 20 – x
Putting value of y in (1), we get
37x + 53(20 – x) = 820
37x + 1060 – 53x = 820
16x = 240
\(x=\frac { 240 }{ 16} =15 \)
From (3), y = 20 – x = 20 – 15 = 5
x = 15, y = 5
Thus, cost of a pen = Rs 15 and cost of pencil = Rs 5
Question 3:
Let the number of 20 P and 25 P coins be x and y respectively
Total number of coins x + y = 50
i.e., x + y = 50 —(1)

Multiplying (1) by 5 and (2) by 1, we get
5x + 5y = 250 —(3)
4x + 5y = 230 —(4)
Subtracting (4) from (3), we get
x = 20
Putting x = 20 in (1),
y = 50 – x
= 50 – 20
= 30
Hence, number of 20 P coins = 20 and number of 25 P coins = 30
Question 4:
Let the two numbers be x and y respectively.
Given:
x + y = 137 —(1)
x – y = 43 —(2)
Adding (1) and (2), we get
2x = 180
\(y=\frac { 180 }{ 2} =90 \)
Putting x = 90 in (1), we get
90 + y = 137
y = 137 – 90
= 47
Hence, the two numbers are 90 and 47.
Question 5:
Let the first and second number be x and y respectively.
According to the question:
2x + 3y = 92 —(1)
4x – 7y = 2 —(2)
Multiplying (1) by 7 and (2) by 3, we get
14 x+ 21y = 644 —(3)
12x – 21y = 6 —(4)
Adding (3) and (4), we get
\(26x=650\\ x=\frac { 650 }{ 26 } =25 \)[/latex]
Putting x = 25 in (1), we get
2 × 25 + 3y = 92
50 + 3y = 92
3y = 92 – 50
\(y=\frac { 42 }{ 3 } =14 \)
y = 14
Question 6:
Let the first and second numbers be x and y respectively.
According to the question:
3x + y = 142 —(1)
4x – y = 138 —(2)
Adding (1) and (2), we get
\(7x=280\\x=\frac { 280 }{ 7 } =40 \)
Putting x = 40 in (1), we get
3 × 40 + y = 142
y = 142 – 120
y = 22
Hence, the first and second numbers are 40 and 22.
Question 7:
Let the greater number be x and smaller be y respectively.
According to the question:
2x – 45 = y
2x – y = 45 —(1)
and
2y – x = 21
-x + 2y = 21 —(2)
Multiplying (1) by 2 and (2) by 1
4x – 2y = 90 —(3)
-x + 2y = 21 —(4)
Adding (3) and (4), we get
3x = 111
\(x=\frac { 111 }{ 3 } =37 \)
Putting x = 37 in (1), we get
2 × 37 – y = 45
74 – y = 45
y = 29
Hence, the greater and the smaller numbers are 37 and 29.
Question 8:
Let the larger number be x and smaller be y respectively.
We know,
Dividend = Divisor × Quotient + Remainder
3x = y × 4 + 8
3x – 4y = 8 —(1)
And
5y = x × 3 + 5
-3x + 5y = 5 —(2)
Adding (1) and (2), we get
y = 13
putting y = 13 in (1)

Hence, the larger and smaller numbers are 20 and 13 respectively.
Question 9:
Let the required numbers be x and y respectively.
Then,

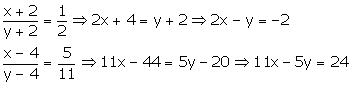
Therefore,
2x – y = -2 —(1)
11x – 5y = 24 —(2)
Multiplying (1) by 5 and (2) by 1
10x – 5y = -10 —(3)
11x – 5y = 24 —(4)
Subtracting (3) and (4) we get
x = 34
putting x = 34 in (1), we get
2 × 34 – y = -2
68 – y = -2
-y = -2 – 68
y = 70
Hence, the required numbers are 34 and 70.
Question 10:
Let the numbers be x and y respectively.
According to the question:

x – y = 14 —(1)
From (1), we get
x = 14 + y —(3)
putting x = 14 + y in (2), we get

Putting y = 9 in (1), we get
x – 9 = 14
x = 14 + 9 = 23
Hence the required numbers are 23 and 9
Question 11:
Let the ten’s digit be x and units digit be y respectively.
Then,
x + y = 12 —(1)
Let the ten’s digit of required number be x and its unit’s digit be y respectively
Required number = 10x + y
10x + y = 7(x + y)
10x + y = 7x + 7y
3x – 6y = 0 —(1)
Number found on reversing the digits = 10y + x
(10x + y) – 27 = 10y + x
10x – x + y – 10y = 27
9x – 9y = 27
(x – y) = 27
x – y = 3 —(2)
Multiplying (1) by 1 and (2) by 6
3x – 6y = 0 —(3)
6x – 6y = 18 —(4)
Subtracting (3) from (4), we get
\(3x=18\\ x=\frac { 18 }{ 3 } =6 \)
Putting x = 6 in (1), we get
3 × 6 – 6y = 0
18 – 6y = 0
\(-6y=-18\\ y=\frac { -18 }{ -6 } =3 \)
Number = 10x + y
= 10 × 6 + 3
= 60 + 3
= 63
Hence the number is 63.
Question 12:
Let the ten’s digit and unit’s digits of required number be x and y respectively.
Required number = 10x + y
Number obtained on reversing digits = 10y + x
According to the question:
10y + x × (10x + y) = 18
10y + x – 10x – y = 18
9y – 9x = 18
y – x = 2 —-(2)
Adding (1) and (2), we get
\(2y=14\\ y=\frac { 14 }{ 2 } =7 \)
Putting y = 7 in (1), we get
x + 7 = 12
x = 5
Number = 10x + y
= 10 × 5 + 7
= 50 + 7
= 57
Hence, the number is 57.
Question 13:
Let the ten’s digit and unit’s digits of required number be x and y respectively.
Then,
x + y = 15 —(1)
Required number = 10x + y
Number obtained by interchanging the digits = 10y + x
10y + x × (10x + y) = 9
10y + x – 10x – y = 9
9y – 9x = 9

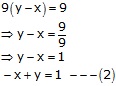
Add (1) and (2), we get
\(2y=16\\ y=\frac { 16 }{ 2 } =8 \)
Putting y = 8 in (1), we get
x + 8 = 15
x = 15 – 8 = 7
Required number = 10x + y
= 10 × 7 + 8
= 70 + 8
= 78
Hence the required number is 78.
Question 14:
Let the ten’s and unit’s of required number be x and y respectively.
Then, required number =10x + y
According to the given question:
10x + y = 4(x + y) + 3
10x + y = 4x + 4y + 3
6x – 3y = 3
2x – y = 1 —(1)
And
10x + y + 18 = 10y + x
9x – 9y = -18

x – y = -2 —(2)
Subtracting (2) from (1), we get
x = 3
Putting x = 3 in (1), we get
2 × 3 – y = 1
y = 6 – 1 = 5
x = 3, y = 5
Required number = 10x + y
= 10 × 3 + 5
= 30 + 5
= 35
Hence, required number is 35.
Question 15:
Let the ten’s digit and unit’s digit of required number be x and y respectively.
We know,
Dividend = (divisor × quotient) + remainder
According to the given questiion:
10x + y = 6 × (x + y) + 0
10x – 6x + y – 6y = 0
4x – 5y = 0 —(1)
Number obtained by reversing the digits is 10y + x
10x + y – 9 = 10y + x
9x – 9y = 9
9(x – y) = 9
(x – y) = 1 —(2)
Multiplying (1) by 1 and (2) by 5, we get
4x – 5y = 0 —(3)
5x – 5y = 5 —(4)
Subtracting (3) from (4), we get
x = 5
Putting x = 5 in (1), we get

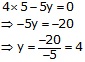
x =5 and y = 4
Hence, required number is 54.
Question 16:
Let the ten’s and unit’s digits of the required number be x and y respectively.
Then, xy = 35
Required number = 10x + y
Also,
(10x + y) + 18 = 10y + x
9x – 9y = -18
9(y – x) = 18 —(1)
y – x = 2
Now,

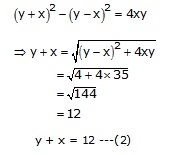
Adding (1) and (2),
2y = 12 + 2 = 14
y = 7
Putting y = 7 in (1),
7 – x = 2
x = 5
Hence, the required number = 5 × 10 + 7
= 57
Question 17:
Let the ten’s and units digit of the required number be x and y respectively.
Then, xy = 14
Required number = 10x + y
Number obtained on reversing the digits = 10y + x
Also,
(10x + y) + 45 = 10y + x
9(y – x) = 45
y – x = 5 —(1)
Now,


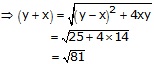
y + x = 9 —(2) (digits cannot be negative, hence -9 is not possible)
On adding (1) and (2), we get
2y = 14
y = 7
Putting y = 7 in (2), we get
7 + x = 9
x = (9 – 7) = 2
x = 2 and y = 7
Hence, the required number is = 2 × 10 + 7
= 27
Question 18:
Let the ten’s and unit’s digits of the required number be x and y respectively.
Then, xy = 18
Required number = 10x + y
Number obtained on reversing its digits = 10y + x
(10x + y) – 63 = (10y + x)
9x – 9y = 63
x – y = 7 —(1)
Now,


Adding (1) and (2), we get

Putting x = 9 in (1), we get
9 – y = 7
y = 9 – 7
y = 2
x = 9, y = 2
Hence, the required number = 9 × 10 + 2
= 92.
Question 19:
Let the ten’s digit be x and the unit digit be y respectively.
Then, required number = 10x + y
According to the given question:
10x + y = 4(x + y)
6x – 3y = 0
2x – y = 0 —(1)
And
10x + y = 2xy —(2)
Putting y = 2x from (1) in (2), we get
10x + 2x = 4x² ⇒ 12x – 4x² = 0 ⇒ 4x(3 – x) = 0 ⇒ x = 3
Putting x = 3 in (1), we get
2 × 3 – y = 0
y = 6
Hence, the required number = 3 × 10 + 6
= 36.
Question 20:
Let the numerator and denominator of fraction be x and y respectively.
According to the question:
x + y = 8 —(1)
And

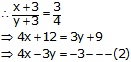
Multiplying (1) be 3 and (2) by 1
3x + 3y = 24 —(3)
4x – 3y = -3 —(4)
Add (3) and (4), we get
\(7x=21\\ x=\frac { 21 }{ 7 } =3 \)
Putting x = 3 in (1), we get
3 + y= 8
y = 8 – 3
y = 5
x = 3, y = 5
Hence, the fraction is \(\frac { x }{ y } =\frac { 3 }{ 5 }  \)
Question 21:
Let numerator and denominator be x and y respectively.
Sum of numerator and denominator = x + y
3 less than 2 times y = 2y – 3
x + y =2y – 3
or x – y = -3 —(1)
When 1 is decreased from numerator and denominator, the fraction becomes:

2(x – 1) = y – 1
or 2x – 2 = y – 1
or 2x – y = 1 —(2)
Subtracting (1) from (2), we get
x = 1 + 3 = 4
Putting x = 4 in (1), we get
y = x + 3
= 4 + 3
= 7
the fraction is \(\frac { x }{ y } =\frac { 4 }{ 7 } \)
Question 22:
Let the numerator and denominator be x and y respectively.
Then the fraction is \(\frac { x }{ y } \)

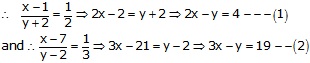
Subtracting (1) from (2), we get
x = 15
Putting x = 15 in (1), we get
2 × 15 – y = 4
30 – y = 4
y = 26
x = 15 and y = 26
Hence the given fraction is \(\frac { 15 }{ 26 } \)
Question 23:
Let the numerator and denominator be x and y respectively.
Then the fraction is \(\frac { x }{ y } \).
According to the given question:
y = x + 11
y – x = 11 —(1)
and

-3y + 4x = -8 —(2)
Multiplying (1) by 4 and (2) by 1
4y – 4x = 44 —(3)
-3y + 4x = -8 —(4)
Adding (3) and (4), we get
y = 36
Putting y = 36 in (1), we get
y – x = 11
36 – x = 11
x = 25
x = 25, y = 36
Hence the fraction is \(\frac { 25 }{ 36 } \)
Question 24:
Let the numerator and denominator be x and y respectively.
Then the fraction is \(\frac { x }{ y } \).

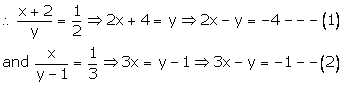
Subtracting (1) from (2), we get
x = 3
Putting x = 3 in (1), we get
2 × 3 – 4
-y = -4 -6
y = 10
x = 3 and y = 10
Hence the fraction is \(\frac { 3 }{ 10 } \)
Question 25:
Let the fraction be \(\frac { x }{ y } \).
When 2 is added to both the numerator and the denominator, the fraction becomes:

3x – y = -4 —(1)
When 3 is added both to the numerator and the denominator, the fractions becomes:

5x – 2y = -9 —-(2)
Multiplying (1) by 2 and (2) by 1, we get
6x – 2y = -8 —(3)
5x – 2y = -9 —(4)
Subtracting (4) from (3), we get
x = 1
Putting x = 1 in (1),
3 × 1 – y = 4
y = 7
Required fraction is \(\frac { 1 }{ 7 } \)
Question 26:
Let the two numbers be x and y respectively.
According to the given question:
x + y = 16 —(1)
And
—(2)
From (2),

xy = 48
We know,

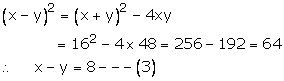
Adding (1) and (3), we get
2x = 24
x = 12
Putting x = 12 in (1),
y = 16 – x
= 16 – 12
= 4
The required numbers are 12 and 4.
Question 27:
Let the present ages of the man and his son be x years and y years respectively.
Then,
Two years ago:
(x – 2) = 5(y – 2)
x – 2 = 5y – 10
x – 5y = -8 —(1)
Two years later:
(x + 2) = 3(y + 2) + 8
x + 2 = 3y + 6 + 8
x – 3y = 12 —(2)
Subtracting (2) from (1), we get
-2y = -20
y = 10
Putting y = 10 in (1), we get
x – 5 × 10 = -8
x – 50 = -8
x = 42
Hence the present ages of the man and the son are 42 years and 10 respectively.
Question 28:
Let the present ages of A and B be x and y respectively.
Five years ago:
(x – 5) = 3(y – 5)
x – 5 = 3y – 15
x – 3y = -10 —(1)
Ten years later:
(x + 10) = 2(y + 10)
x + 10 = 2y + 20
x – 2y = 10 —(2)
Subtracting (2) from (1), we get
y = 20
Putting y = 20 in (1), we get
x – 3y = -10
x – 3 × 20 = -10
x = -10 + 60 = 50
x = 50, y = 20
Hence, present ages of A and B are 50 years and 20 years respectively.
Question 29:
Let the present ages of woman and daughter be x and y respectively.
Then,
Their present ages:
x = 3y + 3
x – 3y = 3 —(1)
Three years later:
(x + 3) = 2(y + 3) + 10
x + 3 = 2y + 6 + 10
x – 2y = 13 —(2)
Subtracting (2) from (1), we get
y = 10
Putting y = 10 in (1), we get
x – 3 × 10 = 3
x = 33
x = 33, y = 10
Hence, present ages of woman and daughter are 33 and 10 years.
Question 30:
Let the present ages of the mother and her son be x and y respectively.
According to the given question:
x + 2y = 70 —(1)
and
2x + y = 95 —(2)
Multiplying (1) by 1 and (2) by 2, we get
x + 2y = 70 —(3)
4x + 2y = 190 —(4)
Subtracting (3) from (4), we get
\(3x=120\\ y=\frac { 120 }{ 3 } =40 \)
Putting x = 40 in (1), we get
40 + 2y = 70
2y = 30
y = 15
x = 40, y = 15
Hence, the ages of the mother and the son are 40 years and 15 years respectively.
Question 31:
Let the present age of the man and the sum of the ages of the two sons be x and y respectively.
We are given x = 3y —(1)
After 5 years the age of man = x + 5
And age of each son is increased by 5 years
Age of two sons after 5 years = y + 5 + 5 = y + 10
Now,
x + 5 = 2(y + 10)
or x + 5 = 2y + 10
x – 2y = 15 —(2)
Putting x = 3y in (2)
3y – 2y = 15
y = 15
Putting y = 15 in (1),
x = 3 × 15 = 45
Age of the man = 45 years.
Question 32:
Let the present age of the man and his son be x and y respectively.
Ten years later:
(x + 10) = 2(y + 10)
x + 10 = 2y + 20
x – 2y = 10 —(1)
Ten years ago:
(x – 10) = 4(y – 10)
x – 10 = 4y – 40
x – 4y = – 30 —(2)
Subtracting (1) from (2), we get
-2y = -40
y = 20 years
Putting y = 20 in (1), we get
x – 2 × 20 = 10
x = 50
x = 50 years, y = 20 years
Hence, present ages of the man and his son are 50 years and 20 years respectively.
Question 33:
Let the monthly income of A and B be Rs. 5x and Rs. 4x respectively and let their expenditures be Rs. 7y and Rs. 5y respectively.
Then,
5x – 7y = 3000 —(1)
4x – 5y = 3000 —(2)
Multiplying (1) by 5 and (2) by 7 we get
25x – 35y = 15000 —(3)
28x – 35y = 21000 —(4)
Subtracting (3) from (4), we get
3x = 6000
x = 2000
Putting x = 2000 in (1), we get
5 × 2000 – 7y = 3000
-7y = 3000 – 10000
\(y=\frac { -7000 }{ -7 } =1000 \)
x = 2000, y = 1000
Income of A = 5x = 5 × 2000 = Rs. 10000
Income of B = 4x = 4 × 2000 = Rs. 8000
Question 34:
Let Rs. x and Rs. y be the CP of a chair and table respectively
If profit is 25%, then SP of chair =
If profit is 10%, then SP of the table =
SP of a chair and table = Rs. 760

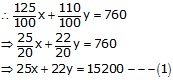
Further , If profit is 10%, then SP of a chair =\(Rs\frac { 110 }{ 100 } x \)
If profit is 25%, then SP of a table =\(Rs\frac { 125 }{ 100 } y \)
SP of a chair and table = Rs. 767.50

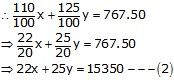
Adding (1) and (2),

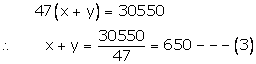
Subtracting (2) from (1)

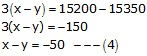
Adding (3) and (4),

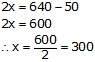
Subtracting (4) from (3)

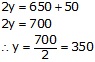
Hence, CP of a chair is Rs 300 and CP of table is Rs 350.
Question 35:
Let the CP of TV and fridge be Rs x and Rs y respectively.

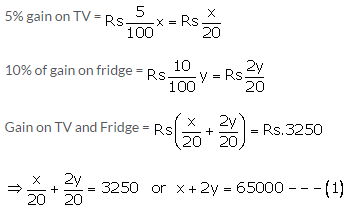
Further,

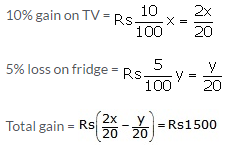
2x – y = 30000 —(2)
Multiplying (2) by 2 and (1) by 1, we get
4x – 2y = 60000 —(3)
x + 2y = 65000 —(4)
Adding (3) and (4), we get
5x = 125000
x = 25000
Putting x = 25000 in (1), we get
25000 + 2y = 65000
2y = 40000
y = 20000
The cost of TV = Rs. 25000 and cost of fridge = Rs. 20000
Question 36:
Let the amounts invested at 12% and 10% be Rs x and Rs y respectively.
Then,
First case:

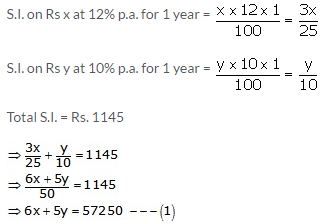
Second case:

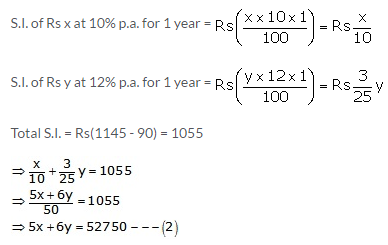
Multiplying (1) by 6 and (2) by 5, we get
36x + 30y = 343500 —(3)
25x + 30y = 263750 —(4)
Subtracting (4) from (3), we get
\(11x=79750\\ x=\frac { 79750 }{ 11 } =7250 \)
Putting x = 7250 in (1), we get
6 × 7250 + 5y = 57250
43500 + 5y = 57250
5y = 13750
y = 2750
x = 7250, y = 2750
Hence, amount invested at 12% = Rs 7250
And amount invested at 10% = Rs 2750
Question 37:
Let the number of student in class room A and B be x and y respectively.
When 10 students are transferred from A to B:
x – 10 = y + 10
x – y = 20 —(1)
When 20 students are transferred from B to A:
2(y – 20) = x + 20
2y – 40 = x + 20
-x + 2y = 60 —(2)
Adding (1) and (2), we get
y = 80
Putting y = 80 in (1), we get
x – 80 = 20
x = 100
Hence, number of students of A and B are 100 and 80 respectively.
Question 38:
Let P and Q be the cars starting from A and B respectively and let their speeds be x km/hr and y km/hr respectively.
Case- I
When the cars P and Q move in the same direction.
Distance covered by the car P in 7 hours = 7x km
Distance covered by the car Q in 7 hours = 7y km
Let the cars meet at point M.

AM = 7x km and BM = 7y km
AM – BM = AB
7x – 7y = 70
7(x – y) = 70
x – y = 10 —-(1)
Case II
When the cars P and Q move in opposite directions.
Distance covered by P in 1 hour = x km
Distance covered by Q in 1 hour = y km
In this case let the cars meet at a point N.

AN = x km and BN = y km
AN + BN = AB
x + y = 70 —(2)
Adding (1) and (2), we get
2x = 80
x = 40
Putting x = 40 in (1), we get
40 – y = 10
y = (40 – 10) = 30
x = 40, y = 30
Hence, the speeds of these cars are 40 km/ hr and 30 km/ hr respectively.
Question 39:
Let the original speed be x km/h and time taken be y hours
Then, length of journey = xy km
Case I:
Speed = (x + 5)km/h and time taken = (y – 3)hour
Distance covered = (x + 5)(y – 3)km
(x + 5) (y – 3) = xy
xy + 5y -3x -15 = xy
5y – 3x = 15 —(1)
Case II:
Speed (x – 4)km/hr and time taken = (y + 3)hours
Distance covered = (x – 4)(y + 3) km
(x – 4)(y + 3) = xy
xy -4y + 3x -12 = xy
3x – 4y = 12 —(2)
Multiplying (1) by 4 and (2) by 5, we get
20y × 12x = 60 —(3)
-20y + 15x = 60 —(4)
Adding (3) and (4), we get
3x = 120
or x = 40
Putting x = 40 in (1), we get
5y – 3 × 40 = 15
5y = 135
y = 27
Hence, length of the journey is (40 × 27) km = 1080 km
Question 40:
Let the speed of train and car be x km/hr and y km/hr respectively.

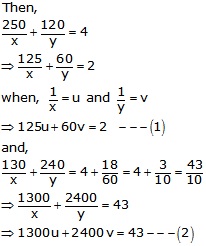
Multiplying (1) by 40 and (2) by 1, we get
5000u + 2400v = 80 —(3)
1300u + 2400v = 43 —(4)
subtracting (4) from (3), we get
\(3700u=37\\ u=\frac { 1 }{ 100 } \)
Putting \(u=\frac { 1 }{ 100 }  \) in (1), we get

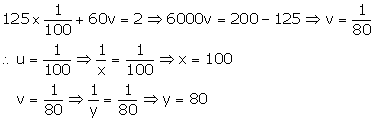
Hence, speeds of the train and the car are 100km/hr and 80 km/hr respectively.
Question 41:
Let the speed of the boat in still water be x km/hr and speed of the stream be y km/hr.
Then,
Speed upstream = (x – y)km/hr
Speed downstream = (x + y) km/hr
Time taken to cover 12 km upstream = \(\frac { 12 }{ x-y } hrs  \)
Time taken to cover 40 km downstream = \(\frac { 40 }{ x+y } hrs  \)
Total time taken = 8hrs

Again, time taken to cover 16 km upstream = \(\frac { 16 }{ x-y }  \)
Time taken to taken to cover 32 km downstream = \(\frac { 32 }{ x+y }  \)
Total time taken = 8hrs

Putting
12u + 40v = 8
3u + 10v = 2 —(1)
and
16u + 32v = 8
2u + 4v = 1 —(2)
Multiplying (1) by 4 and (2) by 10, we get
12u + 40v = 8 —(3)
20u + 40v = 10 —(4)
Subtracting (3) from (4), we get
\(8u=2\\ u=\frac { 1 }{ 4 } \)
Putting \(u=\frac { 1 }{ 4 }  \) in (3), we get

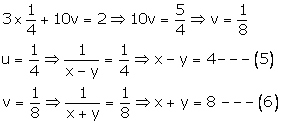
On adding (5) and (6), we get
2x = 12
x = 6
Putting x = 6 in (6) we get
6 + y = 8
y = 8 – 6 = 2
x = 6, y = 2
Hence, the speed of the boat in still water = 6 km/hr and speed of the stream = 2km/hr
Question 42:
Let the fixed charges of taxi per day be Rs x and charges for travelling for 1km be Rs y.
For travelling 110 km, he pays
Rs x + Rs 110y = Rs 1130
x + 110y = 1130 —(1)
For travelling 200 km, he pays
Rs x + Rs 200y = Rs 1850
x + 200y = 1850 —(2)
Subtracting (1) from (2), we get
\(90y=1850-1130=720\\ y=\frac { 720 }{ 90 } =8  \)
Putting y = 8 in (1),
x + 110 × 8 = 1130
x = 1130 – 880 = 250
Hence, fixed charges = Rs 250
And charges for travelling 1 km = Rs 8
Question 43:
Let the fixed hostel charges be Rs x and food charges per day be Rs y respectively.
For student A:
Student takes food for 25days and he has to pay: Rs 3500
Rs x + Rs 25y = Rs 3500
x + 25y = 3500 —(1)
For student B:
Student takes food for 28days and he has to pay: Rs 3800
Rs x + Rs 28y = Rs 3800
or x + 28y = 3800 —(2)
Subtracting (1) from (2), we get
3y = 3800 – 3500
3y= 300
y = 100
Putting y = 100 in (1),
x + 25 × 100 = 3500
or x = 3500 – 2500
or x = 1000
Thus, fixed charges for hostel = Rs 1000 and
Charges for food per day = Rs 100
Question 44:
Let the length = x meters and breadth = y meters
Then,
x = y + 3
x – y = 3 —-(1)
Also,
(x + 3)(y – 2) = xy
3y – 2x = 6 —-(2)
Multiplying (1) by 2 and (2) by 1
-2y + 2x = 6 —(3)
3y – 2x = 6 —(4)
Adding (3) and (4), we get
y = 12
Putting y = 12 in (1), we get
x – 12 = 3
x = 15
x = 15, y = 12
Hence length = 15 metres and breadth = 12 metres
Question 45:
Let the length of a rectangle be x meters and breadth be y meters.
Then, area = xy sq.m
Now,
xy – (x – 5)(y + 3) = 8
xy × [xy × 5y + 3x -15] = 8
xy × xy + 5y × 3x + 15 = 8
3x – 5y = 7 —(1)
And
(x + 3)(y + 2) – xy = 74
xy + 3y +2x + 6 × xy = 74
2x + 3y = 68 —(2)
Multiplying (1) by 3 and (2) by 5, we get
9x – 15y = 21 —(3)
10x + 15y = 340 —(4)
Adding (3) and (4), we get

Putting x = 19 in (3) we get

x = 19 meters, y = 10 meters
Hence, length = 19m and breadth = 10m
Question 46:
Let man’s 1 day’s work be \(\frac { 1 }{ x }  \) and 1 boy’s day’s work be \(\frac { 1 }{ y }  \)
Also let \(\frac { 1 }{ x } =u  \) and \(\frac { 1 }{ y } =v  \)

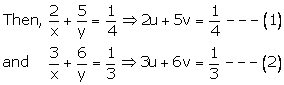
Multiplying (1) by 6 and (2) by 5 we get

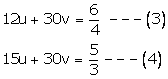
Subtracting (3) from (4), we get

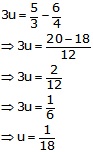
Putting \(u=\frac { 1 }{ 18 }  \) in (1), we get

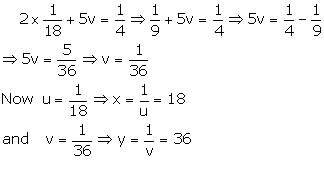
x = 18, y = 36
The man will finish the work in 18 days and the boy will finish the work in 36 days when they work alone.
Question 47:
∠A +∠B + ∠C = 180◦
x + 3x + y = 180
4x + y = 180 —(1)
Also,
3y – 5x = 30
-5x + 3y = 30 —(2)
Multiplying (1) by 3 and (2) by 1, we get
12x + 3y = 540 —(3)
-5x + 3y = 30 —(4)
Subtracting (4) from (3), we get
17x = 510
x = 30
Putting x = 30 in (1), we get
4 × 30 + y = 180
y = 60
Hence ∠A = 30◦, ∠B = 3 × 30◦ = 90◦, ∠C = 60◦
Therefore, the triangle is right angled.
Question 48:
In a cyclic quadrilateral ABCD:
∠A = (x + y + 10)°,
∠B = (y + 20)°,
∠C = (x + y – 30)°,
∠D = (x + y)°
We have, ∠A + ∠C = 180° and ∠B + ∠D = 180°

Now,
∠A + ∠C = (x + y + 10)° + (x + y – 30)° = 180°
2x + 2y – 20° = 180°
x + y – 10° = 90°
x + y = 100 —(1)
Also,
∠B + ∠D = (y + 20)° +(x + y)° = 180°
x + 2y + 20° = 180°
x + 2y = 160° —(2)
Subtracting (1) from (2), we get
y = 160 – 100 = 60
Putting y = 60 in (1), we get
x = 100 – y
x = 100 – 60
x = 40
Therefore,

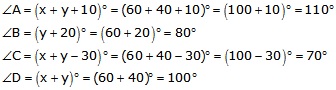
Hope given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables are helpful to complete your math homework.

If you have any doubts, please comment below. A Plus Topper try to provide online math tutoring for you.