Permutations with Repetition
Number of permutations with repetition
(1) The number of permutations (arrangements) of n different objects, taken r at a time, when each object may occur once, twice, thrice,……..upto r times in any arrangement = The number of ways of filling r places where each place can be filled by any one of n objects.

The number of permutations = The number of ways of filling r places = (n)r.
(2) The number of arrangements that can be formed using n objects out of which p are identical (and of one kind) q are identical (and of another kind), r are identical (and of another kind) and the rest are distinct is \(\frac { n! }{ p!q!r! }\).
For permutations with repetition, order still matters.
Hint: When working with “arrangements”, it is often helpful to make a visual of the situation by drawing segments to represent the locations of the items.
Example: How many 3 letter words can be formed using the letters c,a,t allowing for repetition of the letters?
Solution:
For this problem, 3 locations are needed:
_____ • _____ • _____
There are 3 letters which can be used to fill the first location. Because repetition is allowed, the same 3 letters can be used to fill the second location and also the last location.
__3___ • __3___ • __3___ = 27 arrangements

Permutations with Repetition of Indistinguishable Objects:
Indistinguishable objects are simply items (letters) that are repeated in the original set. For example, if the word MOM was used instead of CAT, in the example above, the two letter M’s are indistinguishable from one another, since they repeat. Using MOM, some of our answers would have been duplicates of one another because of the repeating M.
If we are looking for answers that are not duplicates (unique answers), we must deal with any letters (objects) that repeat in the original set.
The number of different permutations of n objects, where there are n1 indistinguishable objects of style 1, n2 indistinguishable objects of style 2, …, and nk indistinguishable objects of style k, is ;
![]()
In general, repetitions are taken care of by dividing the permutation by the factorial of the number of objects that are identical.
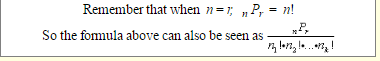
Example:
1. How many different 5-letter words can be formed from the word APPLE ?

2. How many different six-digit numerals can be written using all of the following six digits:
4,4,5,5,5,7
![]()