Partial Fractions

Partial Fractions

An expression of the form \(\frac { f(x) }{ g(x) }\), where f(x) and g(x) are polynomial in x, is called a rational fraction.

1. Proper rational functions: Functions of the form \(\frac { f(x) }{ g(x) }\), where f(x) and g(x) are polynomials and g(x) ≠ 0, are called rational functions of x.
   If degree of f(x) is less than degree of g(x),then is called a proper rational function.
2. Improper rational functions: If degree of f(x) is greater than or equal to degree of g(x), then \(\frac { f(x) }{ g(x) }\) is called an improper rational function.
3. Partial fractions: Any proper rational function can be broken up into a group of different rational fractions, each having a simple factor of the denominator of the original rational function. Each such fraction is called a partial fraction.

If by some process, we can break a given rational function \(\frac { f(x) }{ g(x) }\) into different fractions, whose denominators are the factors of g(x),then the process of obtaining them is called the resolution or decomposition of \(\frac { f(x) }{ g(x) }\) into its partial fractions.

Different cases of partial fractions

(1) When the denominator consists of non-repeated linear factors:
To each linear factor (x – a) occurring once in the denominator of a proper fraction, there corresponds a single partial fraction of the form \(\frac { A }{ x-a }\), where A is a constant to be determined.
If g(x) = (x – a₁)(x – a₂)(x – a₃) ……. (x – a_n), then we assume that,

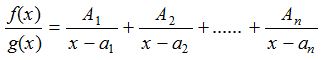
where A₁, A₂, A₃, ………. A_n are constants, can be determined by equating the numerator of L.H.S. to the numerator of R.H.S. (after L.C.M.) and substituting x = a₁, a₂,…… a_n.
(2) When the denominator consists of linear factors, some repeated:
To each linear factor (x – a) occurring r times in the denominator of a proper rational function, there corresponds a sum of r partial fractions.
Let g(x) = (x – a)^k(x – a₁)(x – a₂) ……. (x – a_r). Then we assume that

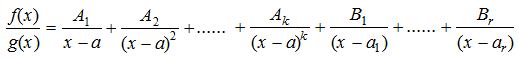
Where A₁, A₂, A₃, ………. A_k are constants. To determine the value of constants adopt the procedure as above.
(3) When the denominator consists of non-repeated quadratic factors:
To each irreducible non repeated quadratic factor ax² + bx + c, there corresponds a partial fraction of the form \(\frac { Ax+B }{ { a{ x }^{ 2 }+bx+c } }\), where A and B are constants to be determined.
Example :

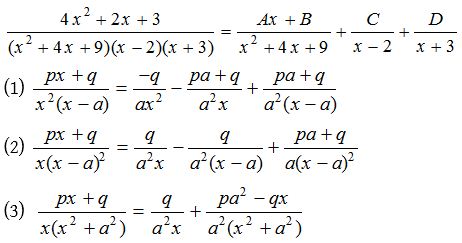
(4) When the denominator consists of repeated quadratic factors:
To each irreducible quadratic factor ax² + bx + c occurring r times in the denominator of a proper rational fraction there corresponds a sum of r partial fractions of the form.

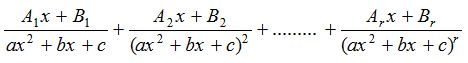
where, A’s and B’s are constants to be determined.

Partial fractions of improper rational functions

If degree of is greater than or equal to degree of g(x), then \(\frac { f(x) }{ g(x) }\) is called an improper rational function and every rational function can be transformed to a proper rational function by dividing the numerator by the denominator.
We divide the numerator by denominator until a remainder is obtained which is of lower degree than the denominator.

General method of finding out the constants

1. Express the given fraction into its partial fractions in accordance with the rules written above.
2. Then multiply both sides by the denominator of the given fraction and you will get an identity which will hold for all values of x.
3. Equate the coefficients of like powers of x in the resulting identity and solve the equations so obtained simultaneously to find the various constant is short method. Sometimes, we substitute particular values of the variable x in the identity obtained after clearing of fractions to find some or all the constants. For non-repeated linear factors, the values of x used as those for which the denominator of the corresponding partial fractions become zero.