NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 3 Pair of Linear Equations in Two Variables Class 10 NCERT Solutions Ex 3.4.
- Pair of Linear Equations in Two Variables Class 10 Ex 3.1
- Pair of Linear Equations in Two Variables Class 10 Ex 3.2
- Pair of Linear Equations in Two Variables Class 10 Ex 3.3
- Pair of Linear Equations in Two Variables Class 10 Ex 3.5
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | Pair of Linear Equations in Two Variables |
| Exercise | Ex 3.4 |
| Number of Questions Solved | 2 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
Page No: 56
Question 1. Solve the following pair of linear equations by the elimination method and the substitution method:
(i) x + y =5 and 2x –3y = 4
(ii) 3x + 4y = 10 and 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7
(iv) x/2 + 2y/3 = – 1 and x – y/3 = 3
Solution:

(ii) Elimination method:
3x + 4y = 10 …(1)
2x – 2y = 2 …(2)
Multiplying equation (2) by 2, we obtain:
4x – 4y = 4 …(3)
Adding equation (1) and (3), we obtain
7x = 14
x = 2
Substituting the value of x in equation (1), we obtain:
6 + 4y = 10
4y = 4
y = 1
Hence, x = 2, y = 1
Substitution method:
From equation (2), we obtain:
x = 1 + y …(4)
Putting this value in equation (1), we obtain:
3(1 + y) + 4y = 10.
7y = 7
y = 1
Substituting the value of y in equation (4), we obtain:
x = 1+1 = 2
∴ x = 2, y = 1

Substitution method:
From equation (1), we obtain:
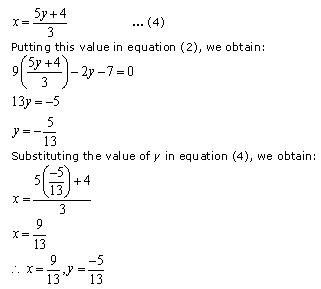
Substitution method:
From equation (2), we obtain:
y = 3x – 9 … (3)
Putting this value in equation (1), we obtain:
3x + 4(3x – 9) = -6
15x = 30
x = 2
Substituting the value of x in equation (3), we obtain:
y = 6 – 9 = -3
∴ x = 2 , y = -3
In order to solve the given pair of equations by substitution method, we need to substitute the value of any one of the variable from any one of the equation. The trick here is to make sure you substitute the value of that variable which simplifies your calculations. Note that the solution must be same in both the cases.
Page No: 57
Question 2. Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method:
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1/2 if we only add 1 to the denominator. What is the fraction?
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
(iv) Meena went to bank to withdraw Rs 2000. She asked the cashier to give her Rs 50 and Rs 100 notes only. Meena got 25 notes in all. Find how many notes of Rs 50 and Rs 100 she received.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs 27 for a book kept for seven days, while Susy paid Rs 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Solution:
(i) Let the fraction be x/y
According to the question,
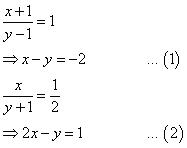
Subtracting equation (1) from equation (2), we obtain:
x = 3
Substituting this value of x in equation (1), we obtain:
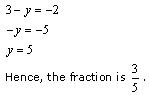
Concept Insight: This problem talks about a fraction. The numerator and denominator of the fraction are not known so we represent these as variables x and y respectively where variable y must be non zero. Then, a pair of linear equations can be formed from the given conditions. The pair of equations can then be solved by eliminating a suitable variable.
(ii) Let present age of Nuri and Sonu be x and y respectively.
According to the question,
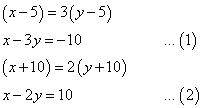
Subtracting equation (1) from equation (2), we obtain:
y = 20
Substituting the value of y in equation (1), we obtain:
x – 60 = -10
x = 50
Thus, the age of Nuri and Sonu are 50 years and 20 years respectively.
Concept Insight: Here, Nuri’s and Sonu’s present age are not known. So, we will write both these in terms of variables. Then, using the given conditions, a pair of linear equations can be formed. The pair of equations can then be solved by eliminating a suitable variable.
(iii) Let the units digit and tens digit of the number be x and y respectively.
Number = 10y + x
Number after reversing the digits = 10x + y
According to the question,
x + y = 9 … (1)
9(10y + x) = 2(10x + y)
88y – 11x = 0
– x + 8y =0 … (2)
Adding equations (1) and (2), we obtain:
9y = 9
y = 1
Substituting the value of y in equation (1), we obtain:
x = 8
Thus, the number is 10y + x = 10 x 1 + 8 = 18
Concept Insight: This problem talks about a two digit number. Here, remember that a two digit number xy can be expanded as 10x + y. Then, using the two given conditions, a pair of linear equations can be formed which can be solved by eliminating one of the variables.
(iv) Let the number of Rs 50 notes and Rs 100 notes be x and y respectively.
According to the question,
x + y = 25 —- (1)
50x + 100y = 2000 —-(2)
Multiplying equation (1) by 50, we obtain:
50x + 50 y = 1250
Subtracting equation (3) from equation (2), we obtain:
50y = 750
y = 15
Substituting the value of y in equation (1), we obtain:
x = 10
Hence, Meena received 10 notes of Rs 50 and 15 notes of Rs 100.
Concept Insight:This problem talks about two types of notes, Rs 50 notes and Rs 100 notes. And the number of both these notes with Meena is not known. So, we denote the number of Rs 50 notes and Rs 100 notes by variables x and y respectively. Now two linear equations can be formed by the given conditions which can be solved by eliminating one of the variables.
(v) Let the fixed charge for first three days and each day charge thereafter be Rs x and Rs y respectively.
According to the question,
x + 4y = 27 —–(1)
x + 2y = 21 —–(2)
Subtracting equation (2) from equation (1), we obtain:
2y = 6
y = 3
Substituting the value of y in equation (1), we obtain:
x + 12 = 27
x = 15
Hence, the fixed charge is Rs 15 and the charge per day is Rs 3.
Concept Insight: Here, the fixed charges for the first three days and per day charges are not known so, they will be represented using two different variables. The two equations can then be obtained by using the given conditions which can be solved by eliminating one of the variables.
We hope the NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4, drop a comment below and we will get back to you at the earliest.