Are you looking for the best Maths NCERT Solutions Chapter 1 Ex 1.1 Class 10? Then, grab them from our page and ace up your preparation for CBSE Class 10 Exams
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 1 Real Numbers Class 10 NCERT Solutions Ex 1.1.
In class 10 chapter 1 real numbers, the concepts like Euclid’s division algorithm, the Fundamental Theorem of Arithmetic, etc. are introduced which are extremely crucial for not only class 10 board exam but are also important for several other important topics which are included in the later grades.
- Real Numbers Class 10 Ex 1.1
- Real Numbers Class 10 Ex 1.2
- Real Numbers Class 10 Ex 1.3
- Real Numbers Class 10 Ex 1.4
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Real Numbers |
| Exercise | Ex 1.1 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1
Page No: 7
Question 1
Use Euclid’s division algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution:
(i) 135 and 225
Step 1: Since 225 > 135, apply Euclid’s division lemma, to a =225 and b=135 to find q and r
such that 225 = 135q+r, 0 ≤ r<135
On dividing 225 by 135 we get quotient as 1 and remainder as 90
i.e 225 = 135 x 1 + 90
You can also Download Class 10 Maths NCERT Solutions to help you to revise complete Syllabus and score more marks in your examinations.
Step 2: Remainder r which is 90 ≠ 0,
we apply Euclid’s division lemma to b =135 and r = 90 to find whole numbers q and r
such that 135 = 90 x q + r, 0 ≤ r<90
On dividing 135 by 90 we get quotient as 1 and remainder as 45
i.e 135 = 90 x 1 + 45
Step 3:Again remainder r = 45 ≠ 0
so we apply Euclid’s division lemma to b =90 and r = 45 to find q and r
such that 90 = 90 x q + r, 0 ≤ r<45
On dividing 90 by 45 we get quotient as 2 and remainder as 0
i.e 90 = 2 x 45 + 0
Step 4: Since the remainder is zero, the divisor at this stage will be HCF of (135, 225).
Since the divisor at this stage is 45, therefore, the HCF of 135 and 225 is 45.
(ii) 196 and 38220
Step 1: Since 38220 > 196, apply Euclid’s division lemma
to a =38220 and b=196 to find whole numbers q and r
such that 38220 = 196 q + r, 0 ≤ r < 196
On dividing 38220 we get quotient as 195 and remainder r as 0
i.e 38220 = 196 x 195 + 0
Since the remainder is zero, divisor at this stage will be HCF
Since divisor at this stage is 196, therefore, HCF of 196 and 38220 is 196.
NOTE: HCF( a,b) = a if a is a factor of b. Here, 196 is a factor of 38220 so HCF is 196.
(iii) 867 and 255
Step 1: Since 867 > 255,
apply Euclid’s division lemma, to a =867 and b=255 to find q and r
such that 867 = 255q + r, 0 ≤ r<255
On dividing 867 by 255 we get quotient as 3 and remainder as 102
i.e 867 = 255 x 3 + 102
Step 2: Since remainder 102 ≠ 0,
we apply the division lemma to a=255 and b= 102 to find whole numbers q and r
such that 255 = 102q + r where 0 ≤ r<102
On dividing 255 by 102 we get quotient as 2 and remainder as 51
i.e 255 = 102 x 2 + 51
Step 3: Again remainder 51 is non zero,
so we apply the division lemma to a=102 and b= 51 to find whole numbers q and r
such that 102 = 51 q + r where 0 r < 51
On dividing 102 by 51 quotient is 2 and remainder is 0
i.e 102 = 51 x 2 + 0
Since the remainder is zero, the divisor at this stage is the HCF
Since the divisor at this stage is 51,therefore, HCF of 867 and 255 is 51.
Concept Insight: To crack such problem remember to apply Euclid’s division Lemma which states that “Given positive integers a and b, there exist unique integers q and r satisfying a = bq + r, where 0 ≤ r < b” in the correct order.
Here, a > b. Euclid’s algorithm works since Dividing ‘a’ by ‘b’, replacing ‘b’ by ‘r’ and ‘a’ by ‘b’ and repeating the process of division till remainder 0 is reached, gives a number which divides a and b exactly.
i.e HCF(a,b) =HCF(b,r)
Note that do not find the HCF using prime factorization in this question when the method is specified and do not skip steps.
Question 2
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution:
Let a be any odd positive integer we need to prove that a is of the form 6q + 1 , or 6q + 3 , or 6q + 5 , where q is some integer. Since a is an integer consider b = 6 another integer applying Euclid’s division lemma
we get a = 6q + r for some integer q ≤ 0, and r = 0, 1, 2, 3, 4, 5 since
0 ≤ r < 6.
Therefore, a = 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4 or 6q + 5
However since a is odd so a cannot take the values 6q, 6q+2 and 6q+4
(since all these are divisible by 2)
Also, 6q + 1 = 2 x 3q + 1 = 2k1 + 1, where k1 is a positive integer
6q + 3 = (6q + 2) + 1 = 2 (3q + 1) + 1 = 2k2 + 1, where k2 is an integer
6q + 5 = (6q + 4) + 1 = 2 (3q + 2) + 1 = 2k3 + 1, where k3 is an integer
Clearly, 6q + 1, 6q + 3, 6q + 5 are of the form 2k + 1, where k is an integer.
Therefore, 6q + 1, 6q + 3, 6q + 5 are odd numbers.
Therefore, any odd integer can be expressed is of the form
6q + 1, or 6q + 3, or 6q + 5 where q is some integer
Concept Insight: In order to solve such problems Euclid’s division lemma is applied to two integers a and b the integer b must be taken in accordance with what is to be proved, for example here the integer b was taken 6 because a must be of the form 6q + 1, 6q + 3, 6q + 5.
Basic definition of even and odd numbers and the fact that addition and, multiplication of integers is always an integer are applicable here.
Question 3
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Maximum number of columns in which the Army contingent and the band can march will be given by HCF (616, 32) We can use Euclid’s algorithm to find the HCF.
Step 1: since 616 > 32 so applying Euclid’s division lemma to a= 616 and b= 32 we get integers q and r as 32 and 19
i.e 616 = 32 x 19 + 8
Step 2: since remainder r =8 ≠ 0 so again applying Euclid’s lemma to 32 and 8 we get integers 4 and 0 as the quotient and remainder i.e 32 = 8 x 4 + 0
Step 3: Since remainder is zero so divisor at this stage will be the HCF.
The HCF (616, 32) is 8.
Therefore, they can march in 8 columns each.
Concept Insight: In order to solve the word problems first step is to interpret the problem and identify what is to be determined. The key word “Maximum” means we need to find the HCF. Do not forget to write the unit in the answer.
Question 4
Use Euclid’s division lemma to show that the square of any positive integer is either of form 3m or 3m + 1 for some integer m.
Solution:
Let a be any positive integer we need to prove that a2 is of the form 3m or 3m + 1 for some integer m.
Let b = 3 be the other integer so applying Euclid’s division lemma to a and b=3
We get a = 3q + r for some integer q ≥ 0and r = 0, 1, 2
Therefore, a = 3q or 3q + 1 or 3q + 2
Now Consider a2
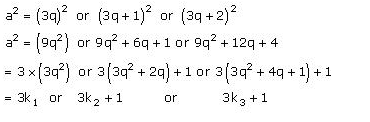
Where k1 = 3q2, k2 =3q2+2q and k3 = 3q2+4q+1 since q ,2,3,1 etc are all integers so is their sum and product.
So k1 k2 k3 are all integers.
Hence, it can be said that the square of any positive integer is either of the form 3m or 3m + 1 for any integer m.
Concept Insight: In order to solve such problems Euclid’s division lemma is applied to two integers a and b the integer b must be taken in accordance with what is to be proved, for example here the integer b was taken 3 because a must be of the form 3m or 3m + 1. Do not forget to take a2. Note that variable is just notation and not the absolute value.
Question 5
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution:
Let a be any positive integer and b = 3
a = 3q + r, where q ≥ 0 and 0≤ r < 3
![]()
Therefore, every number can be represented as these three forms. There are three cases.
Case 1: When a = 3q,
![]()
Where m is an integer such that m = 3q3
Case 2: When a = 3q + 1,
a3 = (3q +1)3
a3 = 27q3 + 27q2 + 9q + 1
a3 = 9(3q3 + 3q2 + q) + 1
a3 = 9m + 1
Where m is an integer such that m = (3q3 + 3q2 + q)
Case 3: When a = 3q + 2,
a3 = (3q +2)3
a3 = 27q3 + 54q2 + 36q + 8
a3 = 9(3q3 + 6q2 + 4q) + 8
a3 = 9m + 8
Where m is an integer such that m = (3q3 + 6q2 + 4q)
Therefore, the cube of any positive integer is of the form 9m, 9m + 1, or 9m + 8.
Concept Insight: In this problem, Euclid’s division lemma can be applied to integers a and b = 9 as well but using 9 will give us 9 values of r and hence as many cases so solution will be lengthy. Since every number which is divisible by 9 is also divisible by 3. so 3 is used. Do not forget to take a3 and all the different values of a i.e
![]()
NCERT Solutions For Class 10 Maths – AplusTopperhttps://t.co/q7hSKh3xmf#NCERTSolutionsForClass10Maths #NCERTSolutions #AplusTopper
— ObulReddy cbse (@ObulReddyCBSE) August 3, 2018
We hope the NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1, drop a comment below and we will get back to you at the earliest.