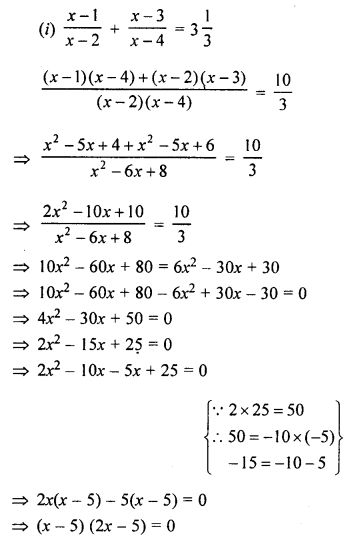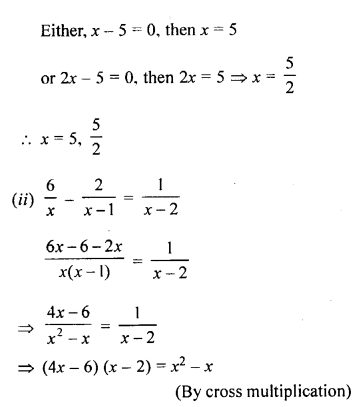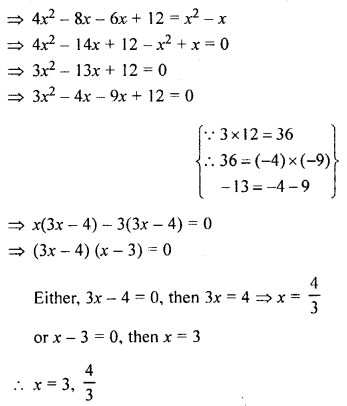ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 7 Quadratic Equations
Question 1.
Solve the following (1 to 12) equations:
(i) x² – 11x + 30 = 0
(ii) 4x² -25 = 0
Solution:
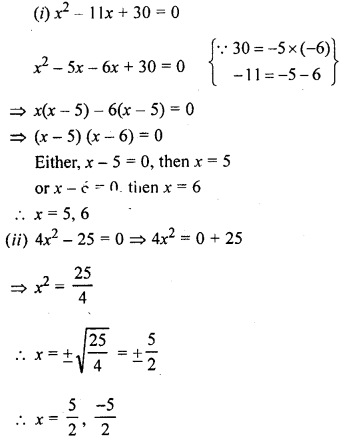
Question 2.
(i) 2x² – 5x = 0
(ii) x² – 2x = 48
Solution:
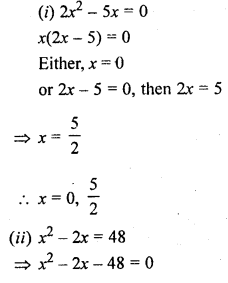
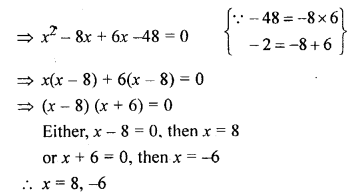
Question 3.
(i) 6 + x = x²
(ii) 2x² + 3x + 1= 0
Solution:
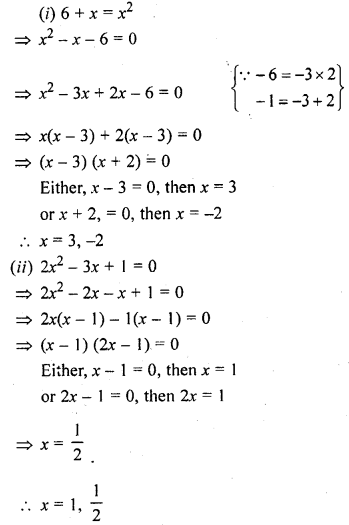
Question 4.
(i) 3x² = 2x + 8
(ii) 4x² + 15 = 16x
Solution:
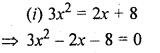
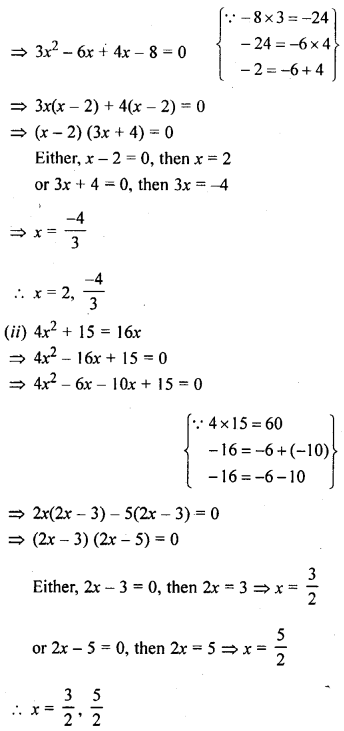
Question 5.
(i) x (2x + 5) = 25
(ii) (x +3) (x – 3) = 40
Solution:
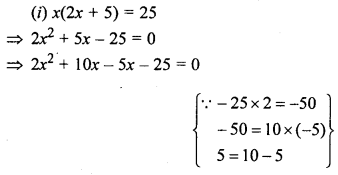
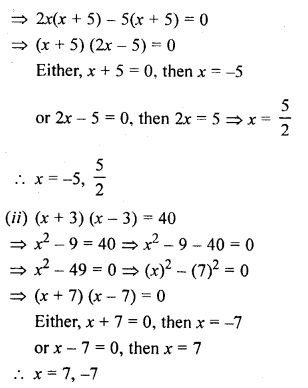
Question 6.
(i) (2x + 3) (x – 4) = 6
(ii) (3x + 1) (2x + 3) = 3
Solution:
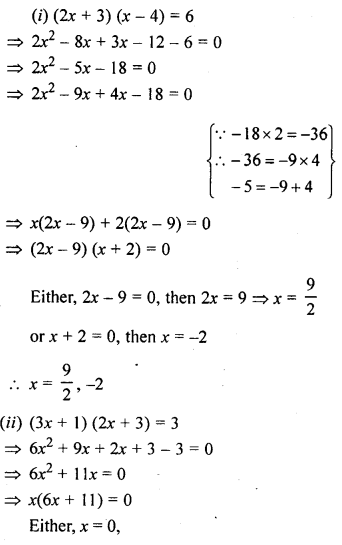
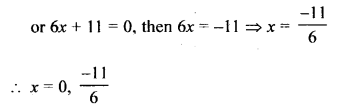
Question 7.
(i) 4x² + 4x + 1 = 0
(ii) (x – 4)² + 5²= 132
Solution:
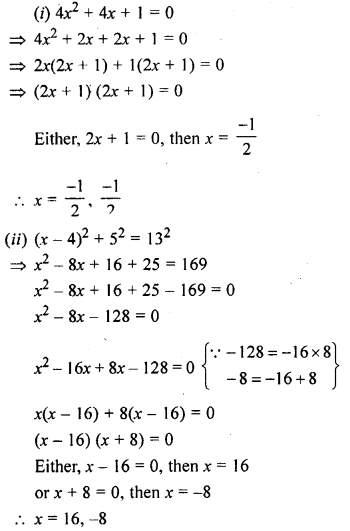
Question 8.
(i) 21x² = 4(2x + 1)
(ii) \(\frac { 2 }{ 3 }\) x2 – \(\frac { 1 }{ 3 }\) x – 1 = 0
Solution:
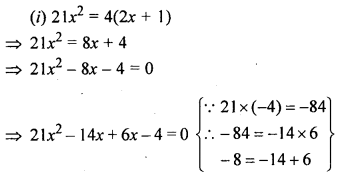
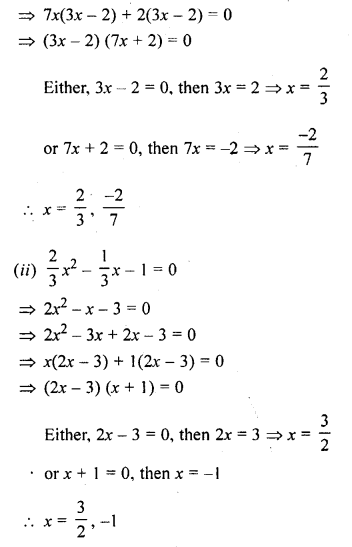
Question 9.
(i) 6x + 29 = \(\frac { 5 }{ x }\)
(ii) x + \(\frac { 1 }{ x }\) = 2 \(\frac { 1 }{ 2 }\)
Solution:
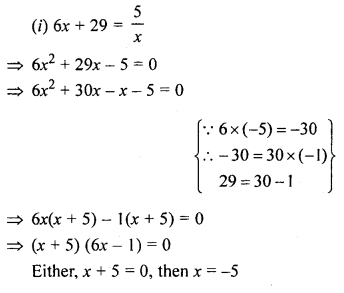
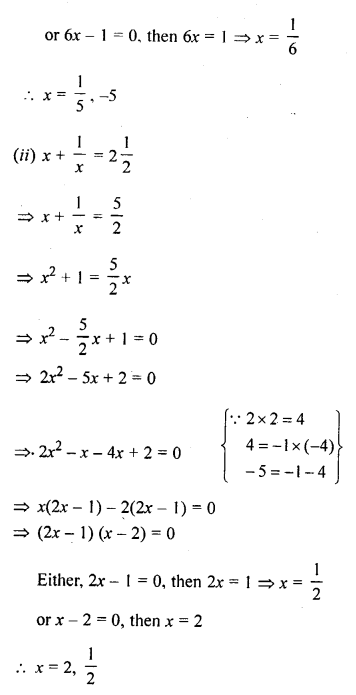
Question 10.
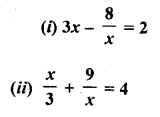
Solution:
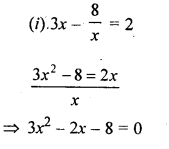
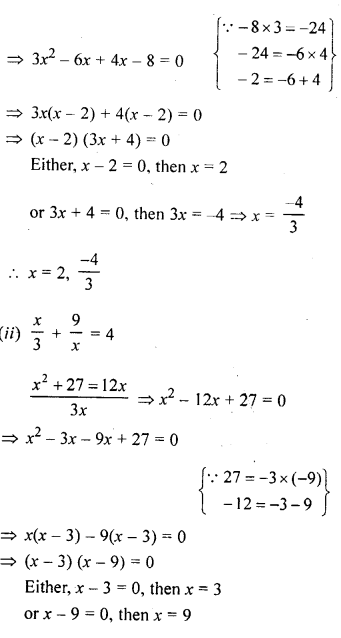
Question 11.
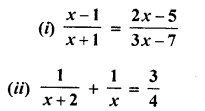
Solution:
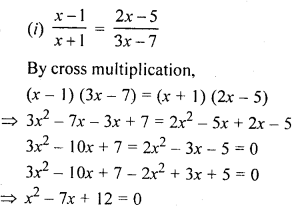

Question 12.

Solution:

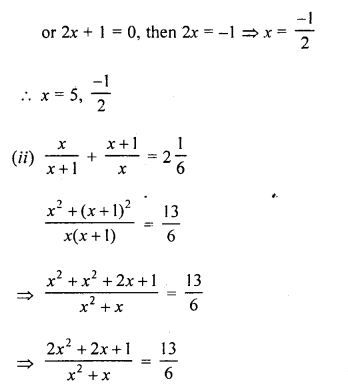
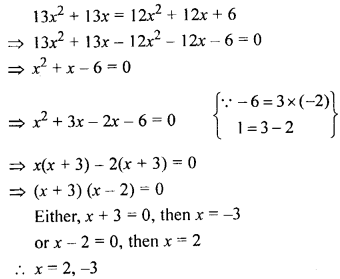
Multiple Choice Questions
Choose the correct Solution from the given four options (1 to 5):
Question 1.
Which of the following is not a quadratic equation :
(a) 2x² = 3x – 5
(b) (2x- 1) (x- 1) = 2x² – 7x + 2
(c) (2x – 1) (x + 2) = (x – 1) (x + 1)
(d) (x+ 1), = x, + 2x+2
Solution:
(2x – 1) (x – 1) = 2x² – 7x + 2 is not a quadratic equation. (b)
Question 2.
If 2 is a root of the quadratic equation 2x² – kx + 1 = 0, then the value of k is

Solution:
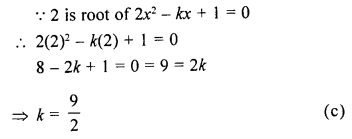
Question 3.
If -3 is a root of the quadratic equation kx² + 2x – 3 = 0, then the value of k is
(a) 1
(b) -1
(c) \(\frac { 1 }{ 9 }\)
(d) \(\frac { 1 }{ -9 }\)
Solution:
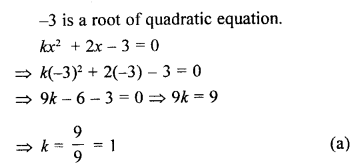
Question 4.
Which of the following quadratic equations has -1 as a root?
(a) x² + 5x + 6 = 0
(b) 2x² – 3x + 1 = 0
(c) 2x² + x – 3 = 0
(d) 2x² – x – 3 = 0
Solution:

Question 5.
The root of the quadratic equation x² – 3x – 4 = 0 are
(a) -4, 1
(b) 4, -1
(c) 4, 1
(d) -4, -1
Solution:
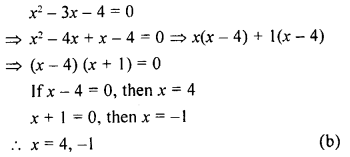
Chapter Test
Solve the following (1 to 3) equations :
Question 1.
(i) x(2x+ 5) = 3
(ii) 3x² – 4x – 4 = 0
Solution:
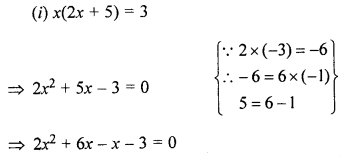
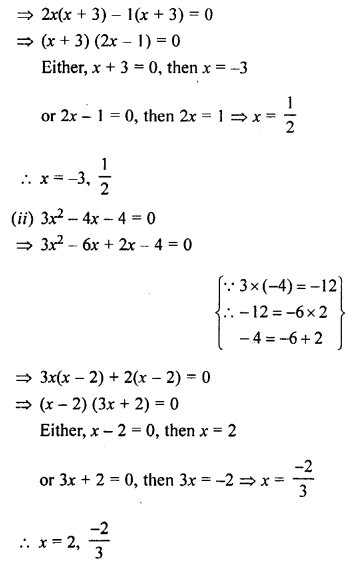
Question 2.
(i) 4x² – 2x + \(\frac { 1 }{ 4 }\) = 0
(ii) 2x² + 7x + 6 = 0
Solution:
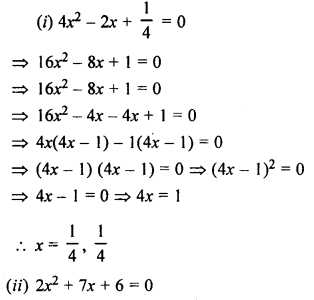
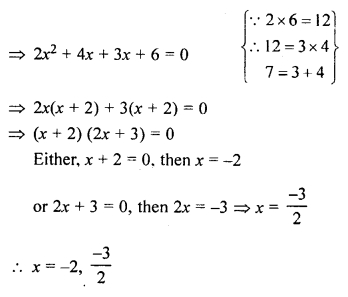
Question 3.
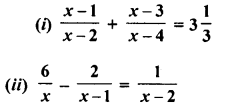
Solution: