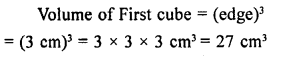ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 16 Mensuration
EXERCISE 16.1
Question 1.
Find the area of a triangle whose base is 6 cm and corresponding height is 4 cm.
Solution:

Question 2.
Find the area of a triangle whose sides are
(i) 3 cm, 4 cm and 5 cm
(ii) 29 cm, 20 cm and 21 cm
(iii) 12 cm, 9.6 cm and 7.2 cm
Solution:


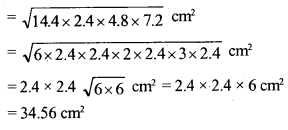
Question 3.
Find the area of a triangle whose sides are 34 cm, 20 cm and 42 cm. Hence, find the length of the altitude corresponding to the shortest side.
Solution:

Question 4.
The sides of a triangular field are 975m, 1050 m and 1125 m. If this field is sold at the rate of Rs. 1000 per hectare, find its selling price. [1 hectare = 10000 m²].
Solution:


Question 5.
The base of a right angled triangle is 12 cm and its hypotenuse is 13 cm long. Find its area and the perimeter.
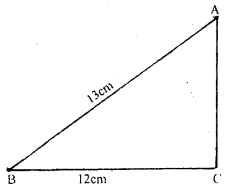
Solution:

Question 6.
Find the area of an equilateral triangle whose side is 8 m. Given your answer correct to two decimal places.
Solution:

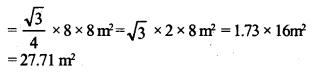
Question 7.
If the area of an equilateral triangle is 81√3 cm² find its. perimeter.
Solution:
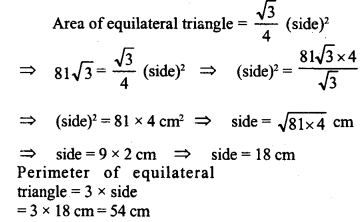
Question 8.
If the perimeter of an equilateral triangle is 36 cm, calculate its area and height.
Solution:
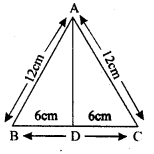

Question 9.
(i) If the length of the sides of a triangle are in the ratio 3:4:5 and its perimeter is 48 cm, find its area.
(ii) The sides of a triangular plot are in the ratio 3: 5:7 and its perimeter is 300 m. Find its area.
Solution:
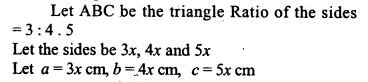

Question 10.
ABC is a triangle in which AB = AC = 4 cm and ∠ A = 90°. Calculate the area of ∆ABC. Also find the length of perpendicular from A to BC.
Solution:
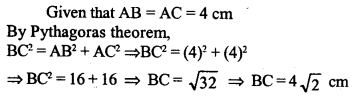
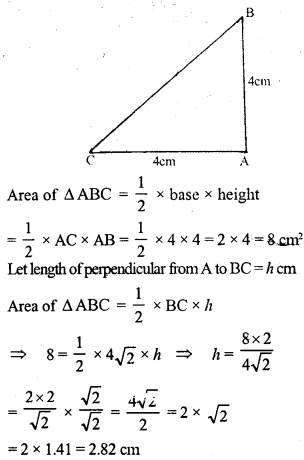
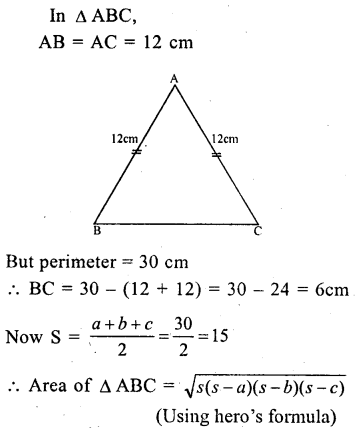
Question 11.
Find the area of an isosceles triangle whose equal sides are 12 cm each and the perimeter is 30 cm.
Solution:
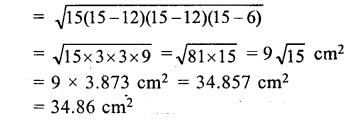
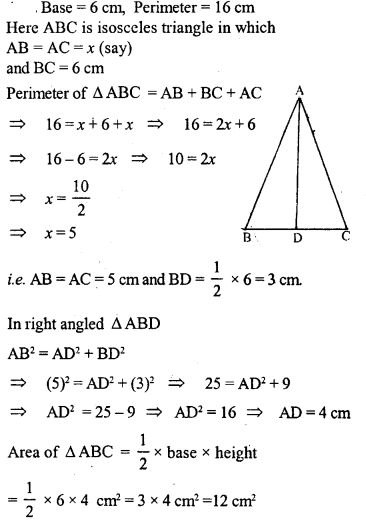
Question 12.
Find the area of an isosceles triangle whose base is 6 cm and perimeter is 16 cm.
Solution:
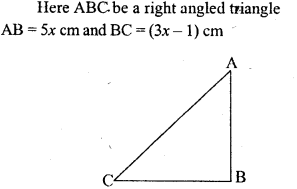
Question 13.
The sides of a right angled triangle containing the right angle are 5x cm and (3x – 1) cm. Calculate the length of the hypotenuse of the triangle if its area is 60 cm².
Solution:

Question 14.
In ∆ ABC, ∠B = 90°, AB = (2A + 1) cm and BC = (A + 1). cm. If the area of the ∆ ABC is 60 cm², find its perimeter.
Solution:


Question 15.
If the perimeter of a right angled triangle is 60 cm and its hypotenuse is 25 cm, find its area.
Solution:

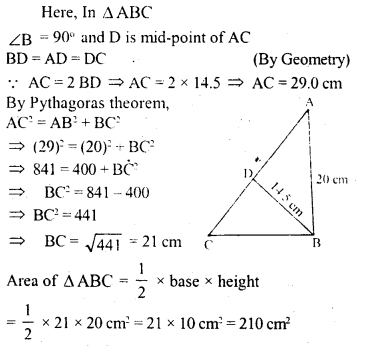
Question P.Q.
In ∆ ABC, ∠B = 90° and D is mid-point of AC. If AB = 20 cm and BD = 14.5 cm, find the area and the perimeter of ∆ ABC.
Solution:
![]()
Question 16.
The perimeter of an isosceles triangle is 40 cm. The base is two third of the sum of equal sides. Find the length of each side.
Solution:
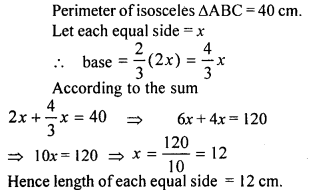
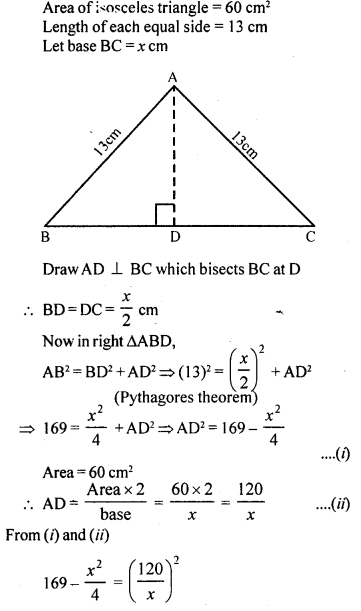
Question 17.
If the area of an isosceles triangle is 60 cm2 and the length of each of its equal sides is 13 cm, find its base.
Solution:

Question 18.
The base of a triangular field is 3 times its height If the cost of cultivating the field at the rate of ₹25 per 100m2 is ₹60000, find its base and height.
Solution:

Question 19.
A triangular park ABC? has sides 120 m, 80 m and 50 m (as shown in the given figure). A gardner Dhania has to put a fence around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹20 per metre leaving a space 3 m wide for a gate on one side.
Solution:
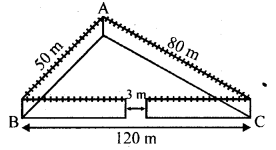
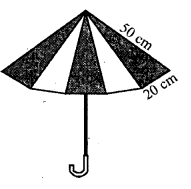
Question 20.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (shown in the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
Solution:

Question 21.
(a) In the figure (1) given below, ABC is an equilateral triangle with each side of length 10 cm. In ∆ BCD, ∠D = 90° and CD = 6 cm.
Find the area of the shaded region. Give your answer correct to one decimal place.
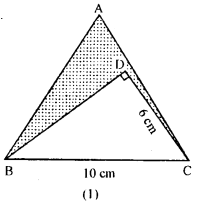
(b) In the figure given, ABC is an isosceles right angled triangle and DEFG is a rectangle. If AD = AE = 3 cm and DB = EC = 4 cm, find the area of the shaded region.
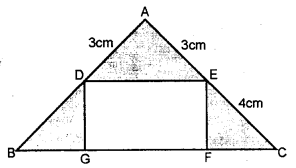
Solution:


EXERCISE 16.2
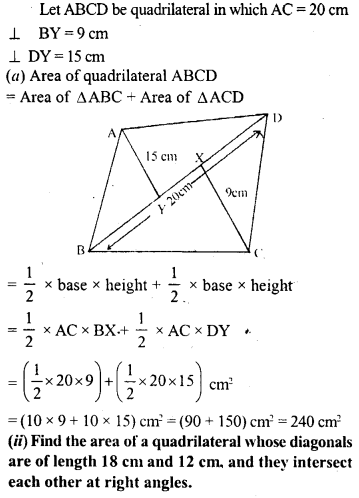
Question 1.
(i) Find the area of quadrilateral whose one diagonal is 20 cm long and the perpendiculars to this diagonal from other vertices are of length 9 cm and 15 cm.
Solution:
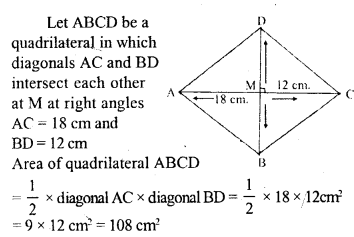
Question 2.
Find the area of the quadrilateral field ABCD whose sides AB = 40 m, BC = 28 m, CD = 15 m, AD = 9 m and ∠A = 90°
Solution:

Question 3.
Find the area of the quadrilateral ABCD in which ∠BCA= 90°, AB = 13 cm and ACD is an equilateral triangle of side 12 cm.
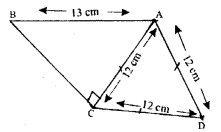
Solution:

Question 4.
Find the area of quadrilateral ABCD in which ∠B = 90°, AB = 6 cm, BC = 8 cm 13 and CD = AD = 13 cm.
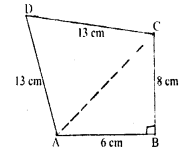
Solution:


Question 5.
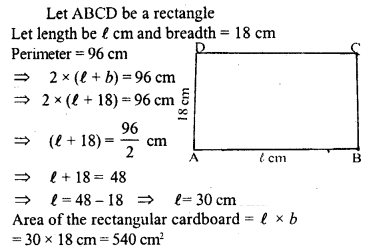
The perimeter of a rectangular cardboard is 96 cm ; If its breadth is 18 cm, find the length and the area of the cardboard.
Solution:
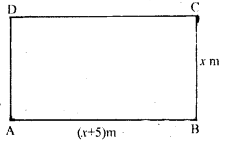
Question 6.
The length of a rectangular hall is 5 m more than its breadth, If the area of the hall is 594 m2, find its perimeter.
Solution:
Let ABCD be rectangular field.

Question 7.
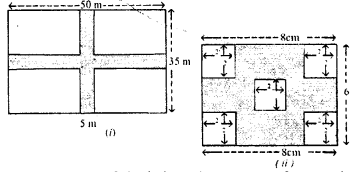
(a) The diagram (i) given below shows two paths drawn inside a rectangular field 50 m long and 35 m wide. The width of each path is 5 metres. Find the area of the shaded portion.
(b) In the diagram (ii) given below, calculate the area of the shaded portion. All measurements are in centimetres.
Solution:
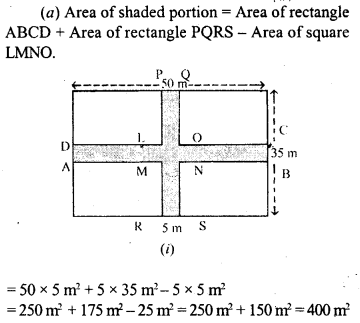
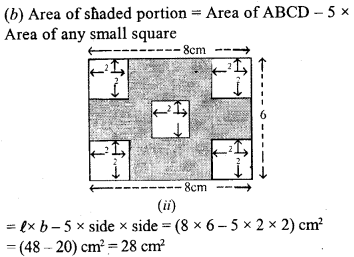
Question 8.
A rectangular plot 20 m long and 14 m wide is to be covered with grass leaving 2 m all around. Find the area to be laid with grass.
Solution:
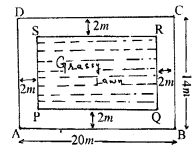

Question 9.
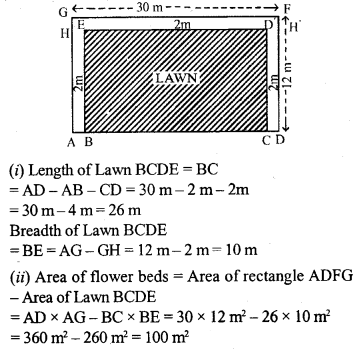
The shaded region of the given diagram represents the lawn in front of a house. On three sides of the lawn there are flower beds of width 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower – beds.
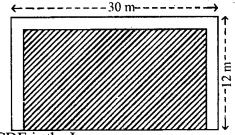
Solution:
BCDE is the lawn
Question 10.
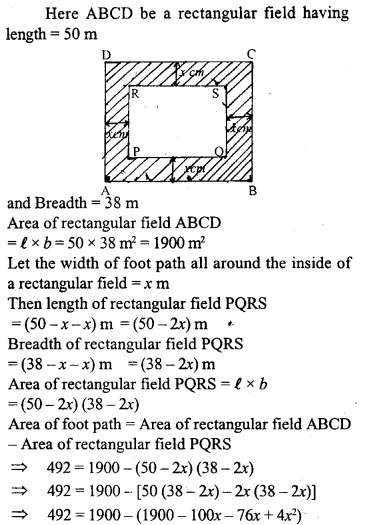
A foot path of uniform width runs all around the inside of a rectangular field 50 m long and 38m wide. If the area of the path is 492 m². Find its width.
Solution:
Question 11.
The cost of enclosing a rectangular garden with a fence all around at the rate of Rs. 15 per metre is Rs. 5400. If the length of the garden is 100 m And the area of the garden.
Solution:

Question 12.
A rectangular floor which measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm find the number of tiles required further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is uncovered?
Solution:

Question 13.
The width of a rectangular room is \(\frac { 3 }{ 5 }\) of its length x metres. If its perimeter isy metres, write an equation connecting.vandy. Find the floor area of the room if its perimeter is 32 m.
Solution:

Question 14.
A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square metres, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x.
Solution:
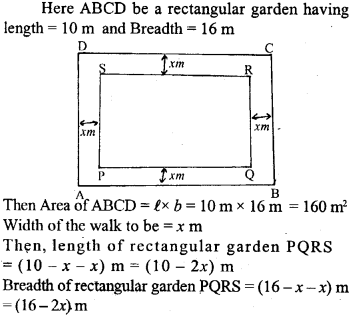
Question 15.
A rectangular room is 6 m long, 4.8 m wide and 3.5 m high. Find the inner surface area of the four walls.
Solution:

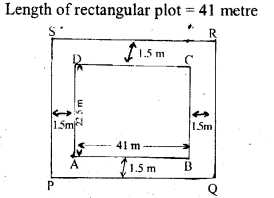
Question 16.
A rectangular plot of land measures 41 metres in length and 22.5 metres in width. A boundary wall 2 metres high is built all around the plot at a distance of 1.5 m from the plot. Find the inner surface area of the boundary wall.
Solution:

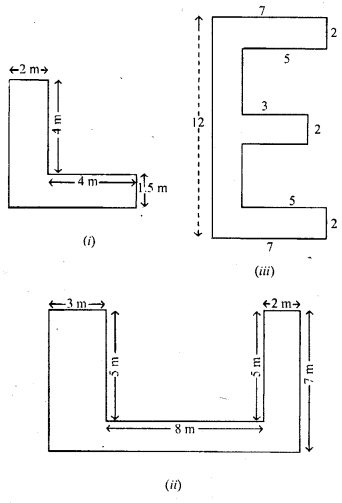
Question 17.
(a) Find the perimeter and area of the figure
(i) given below in which all corners are right angled.
(b) Find the perimeter and area of the figure
(ii) given below in which all corners are right angles.
(c) Find the area and perimeter of the figure
(iii) given below in which all corners are right angles and all measurement in centimetres.
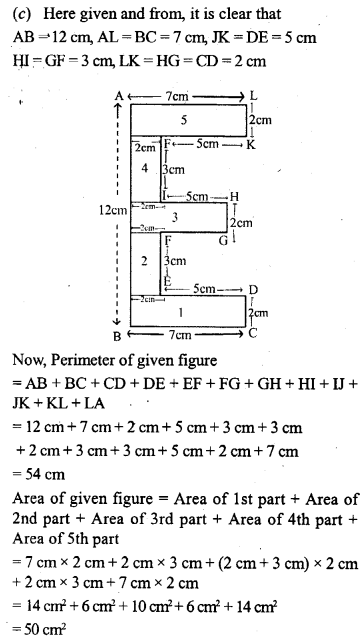
Solution:


Question 18.
The length and the breadth of a rectangle are 12 cm and 9 cm respectively. Find the height of a triangle whose base is 9 cm and whose area is one third that of rectangle.
Solution:
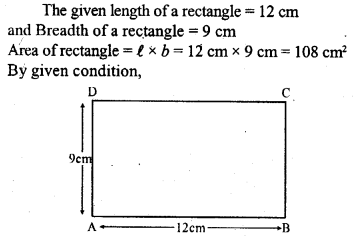

Question 19.
The area of a square plot is 484 mV Find the length of its one side and the length of its one diagonal.
Solution:

Question 20.
A square has the perimeter 56 m. Find its area and the length of one diagonal correct upto two decimal places.
Solution:

Question 21.
A wire when bent in the form of an equilateral triangle encloses an area of 36√3 cm2. Find the area enclosed by the same wire when bent to form:
(i) a square, and
(ii) a rectangle whose length is 2 cm more than its width.
Solution:


Question 22.
Two adjacent sides of a parallelogram are: 15 cm and 10 cm. If the distance between the longer sides is 8 cm, find the area of the parallelogram. Also find the distance between shorter sides.
Solution:
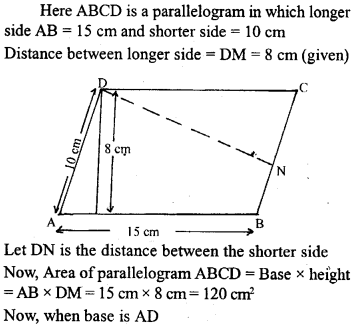

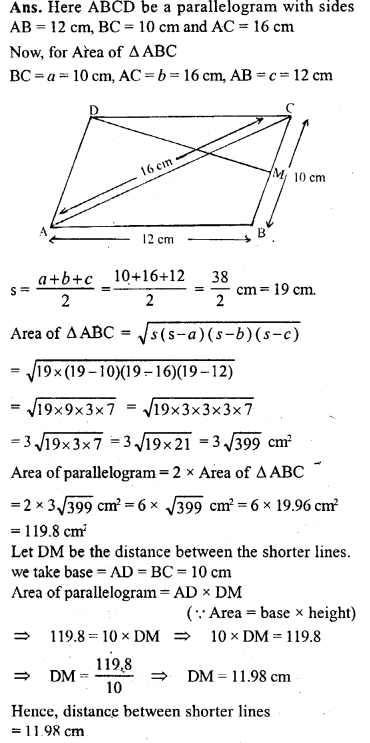
Question 23.
ABCD is a parallelogram with sides AB = 12 cm, BC = 10 cm and diagonal AC = 16 cm. Find the area of the parallelogram. Also find the distance between its shorter sides.
Solution:
Question 24.
Diagonals AC and BD of a parallelogram ABCD intersect at O. Given that AB = 12 cm and perpendicular distance between AB and DC is 6 cm. Calculate the area of the triangle AOD.
Solution:
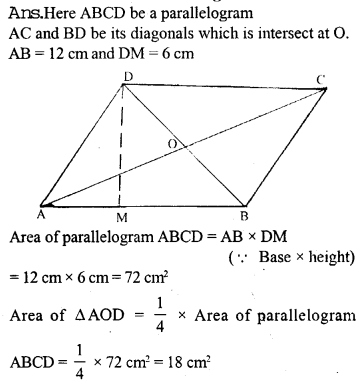
Question 25.
ABCD is a parallelogram with side AB = 10 cm. Its diagonals AC and BD are of length 12 cm and 16 cm respectively. Find the area of the parallelogram ABCD.
Solution:
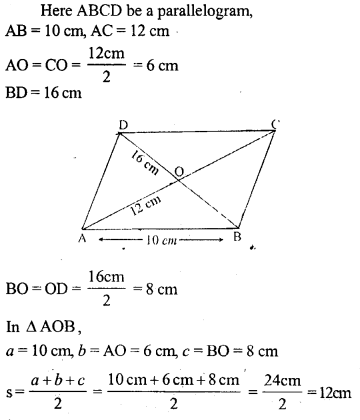

Question 26.
The area of a parallelogram is p cm2 and its height is q cm. A second parallelogram has equal area but its base is ‘r’ cm more than that of the first. Obtain an expression in terms of p, q and r for the height h of the second parallelogram.
Solution:

Question 27.
What is the area of a rhombus whose diagonals are 12 cm and 16 cm ?
Solution:

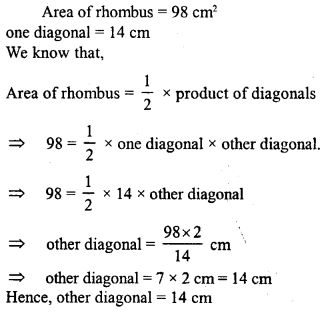
Question 28.
The area of a rhombus is 98 cm². If one of its diagonal is 14 cm, what is the length of the other diagonal?
Solution:
Question 29.
The perimeter of a rhombus is 45 cm. If its height is 8 cm, calculate its area.
Solution:
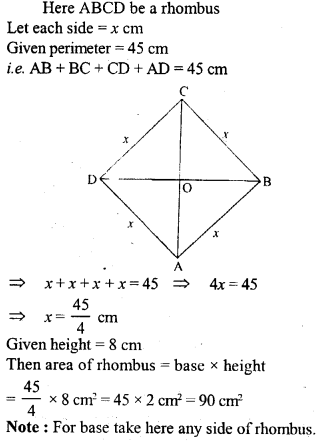
Question 30.
PQRS is a rhombus. If it is given that PQ = 3 cm and the height of the rhombus is 2.5 cm, calculate its area.
Solution:
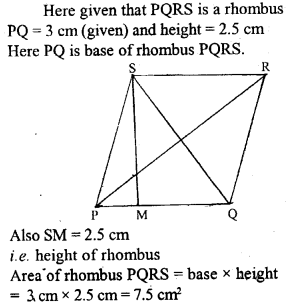
Question 31.
If the diagonals of a rhombus are 8 cm and 6 cm, find its perimeter.
Solution:
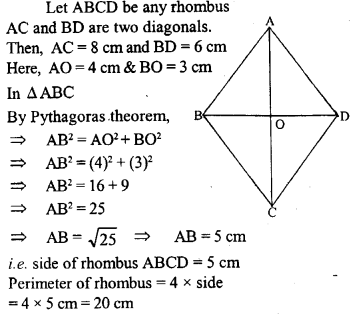
Question 32.
If the sides of a rhombus are 5 cm each and one diagonal is 8 cm, calculate
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
Solution:

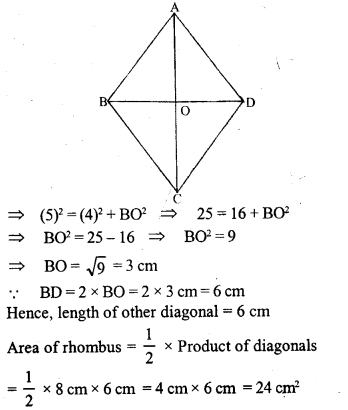
Question 33.
(a) The diagram (t) given below is a trapezium. Find the length of BC and the area of the trapezium Assume AB = 5 cm, AD = 4 cm, CD = 8 cm
(b) The diagram (ii) given below is a trapezium Find (i) AB (ii) area of trapezium ABCD.
(c) The cross-section of a canal is shown in figure (iii) given below. If the canal is 8 m wide at the top and 6 m wide at the bottom and the area of the cross-section is 16.8 m², calculate its depth
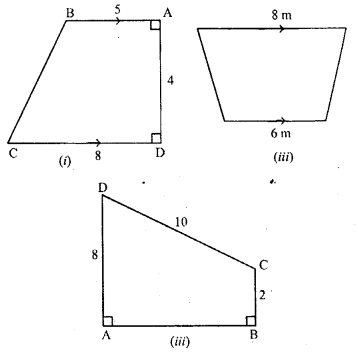
Solution:
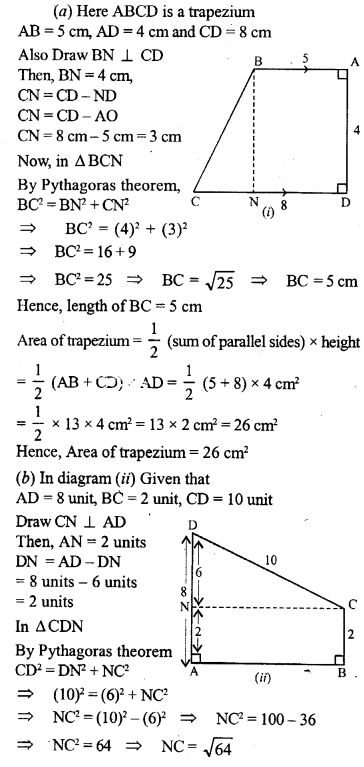

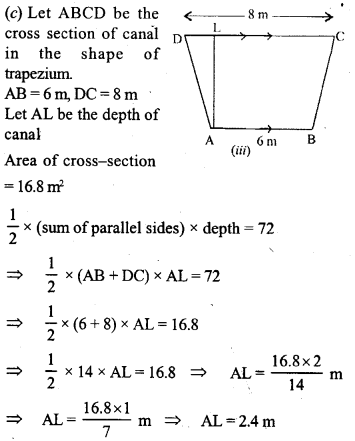
Question 34.
The distance between parallel sides of a trapezium is 12 cm and the distance between mid-points of other sides is 18 cm. Find the area of the trapezium.
Solution:
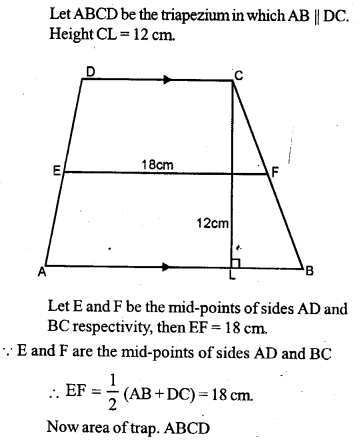
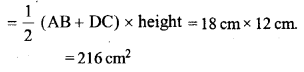
Question 35.
The area of a trapezium is 540 cm². If the ratio of parallel sides is 7 : 5 and the distance between them is 18 cm, find the length of parallel sides.
Solution:

Question 36.
The parallel sides of an isosceles trapezium are in the ratio 2 : 3. If its height is 4 cm and area is 60 cm2, find the perimeter.
Solution:

Question 37.
The area of a parallelogram is 98 cm². If one altitude is half the corresponding base, determine the base and the altitude of the parallelogram.
Solution:

Question 38.
The length of a rectangular garden is 12m more than its breadth. The numerical value of its area is equal to 4 times the numerical value of its perimeter. Find the dimensions of the garden
Solution:

Question 39.
If the perimeter of a rectangular plot is 68 m and length of its diagonal is 26 m, find its area.
Solution:


Question 40.
A rectangle has twice the area of a square. The length of the rectangle is 12 cm greater and the width is 8 cm greater than 2 side of a square. Find the perimeter of the square.
Solution:
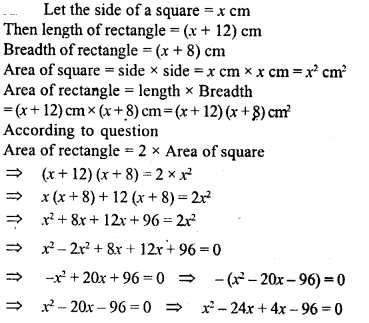
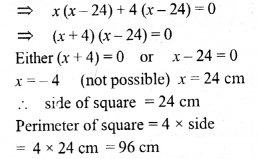
Question 41.
The perimeter of a square is 48 cm. The area of a rectangle is 4 cm2 less than the area of the square. If the length of the rectangle is 4 cm greater than its breadth, find the perimeter of the rectangle.
Solution:

Question 42.
In the adjoining figure, ABCD is a rectangle with sides AB = 10 cm and BC = 8 cm. HAD and BFC are equilateral triangles; AEB and DCG are right angled isosceles triangles. Find the area of the shaded region and the perimeter of the figure.
Solution:
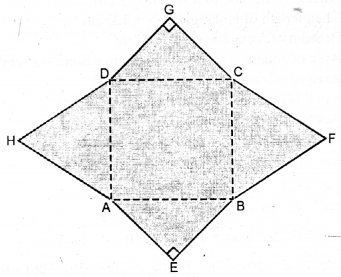

Question 43.
(a) Find the area enclosed by the figure (i) given below, where ABC is an equilateral triangle and DGFG is an isosceles trapezium.
All measurements are in centmetces.
(b) Find the area enclosed by the figure (ii) given below. AH measurements are in centimetres.
(c) In the figure (iii) given below, from a 24. cm x 24 cm piece of cardboard, a block in the shape of letter M is cut off. Find the area of the cardboard left over, all measurements are in centimetres.
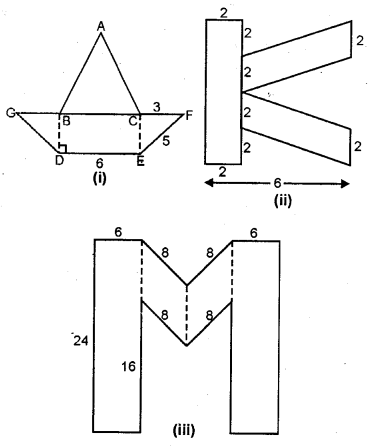
Solution:


Question 44.
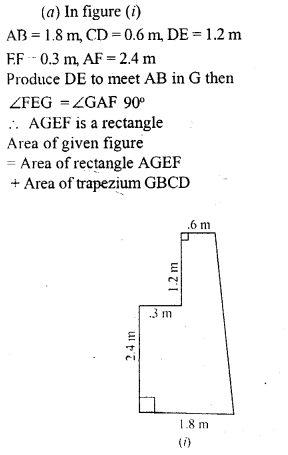
(a) The figure (i) given below shows the cross-section of the concrete structure with the measurements as given. Calculate the area of cross-section.
(b) The figure (ii) given below shows a field with the measurements given in metres. Find the area of the field.
(c) Calculate the area of the pentagon ABCDE shown in fig. (iii) below, given that AX = BX = 6 cm, EY = CY = 4 cm, DE = DC = 5cm,DX = 9cmand DX is perpendicular to EC and AB.
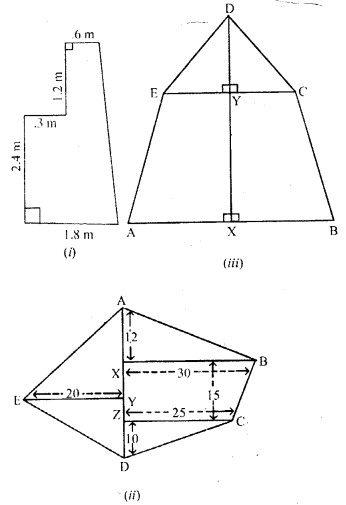
Solution:
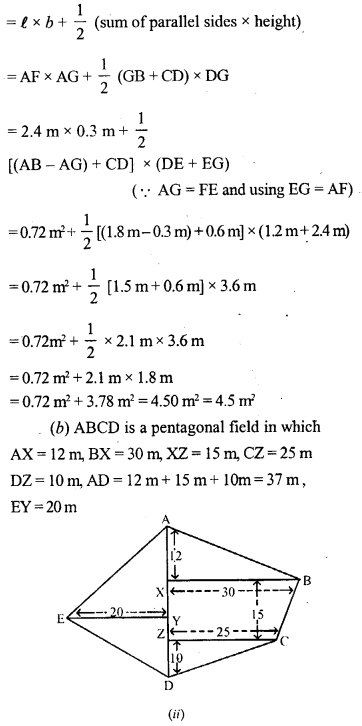

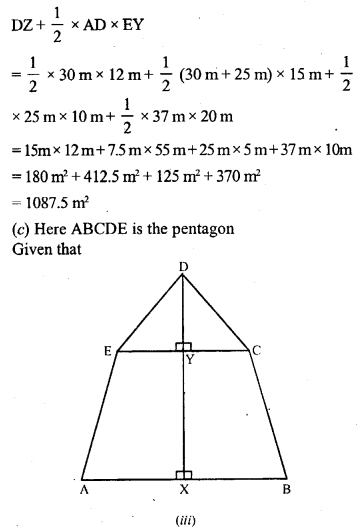

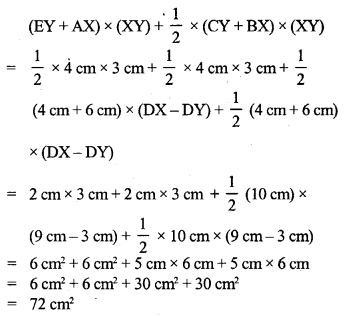
Question 45.
If the length and the breadth of a room are increased by 1 metre the area is increased by 21 square metres. If the length is increased by 1 metre and breadth is decreased by 1 metre the, area is decreased by 5 square metres. Find the perimeter of the room.
Solution:


Question 46.
A triangle and a parallelogram have the same base and same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution:

Question 47.
A rectangle of area 105 cm² has its length equal to x cm. Write down its breadth in terms of x. Given that its perimeter is 44 cm, write down an equation in x and solve it to determine the dimensions of the rectangle.
Solution:

Question 48.
The perimeter of a rectangular plot is 180 m and its area is 1800 m². Take the length of plot as x m. Use the perimeter 180 m to write the value of the breadth in terms of x. Use the value of the length, breadth and the area to,write an equation in x. Solve the equation to calculate the length and breadth of the plot.
Solution:


EXERCISE 16.3
Question 1.
Find the length of the diameter of a circle whose circumference is 44 cm.
Solution:

Question 2.
Find the radius and area of a circle if its circumference is 18π cm.
Solution:
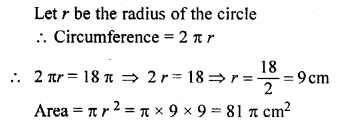
Question 3.
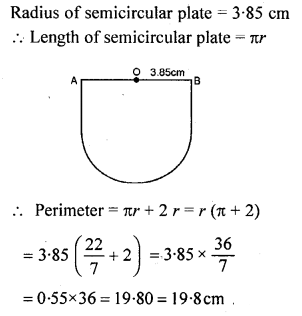
Find the perimeter of a semicircular plate of radius 3.85 cm.
Solution:
Question 4.
Find the radius and circumference of a circle whose area is 144π cm2.
Solution:

Question 5.
A sheet is 11 cm long and 2 cm wide. Circular pieces 0.5 cm in diameter are cut from it to prepare discs. Calculate the number of discs that can be prepared.
Solution:

Question 6.
If the area of a semicircular region is 77cm2, find its perimeter.
Solution:
![]()

Question 7.
(a) In the figure (i) given below, AC and BD are two perpendicular diameters of a circle ABCD. Given that the ara of the shaded portion is 308 cm2, calculate
(i) the length of AC and
(ii) the circumference of the circle.
(b) In the figure (ii) given below, AC and BD are two perpendicular diameters of a circle with centre O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take π = 3.14)
Solution:

Question 8.
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
Solution:
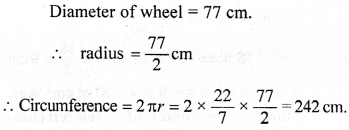
Question 9.
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km/hr. Give your answer correct to the nearest km.
Solution:

Question 10.
The circumference of a circle is 123.2 cm. Calculate :
(i) the radius of the circle in cm.
(ii) the area of the circle in cm2, correct to the nearest cm2.
(iii) the effect on the area of the circle if the radius is doubled.
Solution:


Question 11.
(a) In the figure (i) given below, the area enclosed between the concentric circles is 770 cm2. Given that the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
(b) In the figure (ii) given below, the area enclosed between the circumferences of two concentric circles is 346.5 cm2. The circumference of the inner circle is 88 cm. Calculate the radius of the outer circle.
Solution:


Question 12.
A road 3.5 m wide surrounds a circular plot whose circumference is 44 m. Find the cost of paving the road at ₹50 per m2.
Solution:

Question 13.
The sum of diameters of two circles is 14 cm and the difference of their circumferences is 8 cm. Find the circumference of the two circles.
Solution:

Question 14.
Find the circumference of the circle whose area is equal to the sum of the areas of three circles with radius 2 cm, 3 cm and 6 cm.
Solution:
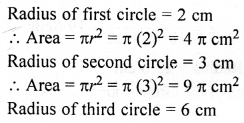

Question 15.
A copper wire when bent in the form of a square encloses an area of 121 cm2. If the same wire is bent into the form of a circle, find the area of the circle.
Solution:

Question 16.
A copper wire when bent into an equilateral triangle has area 121√3 cm2. If the same wire is bent into the form of a circle, find the area enclosed by the wire.
Solution:


Question 17.
(a) Find the circumference of the circle whose area is 16 times the area of the circle with diameter 7 cm.
(b) In the given figure, find the area of the unshaded portion within the rectangle. (Take π = 3.14)
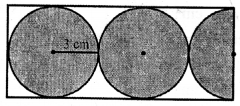
Solution:
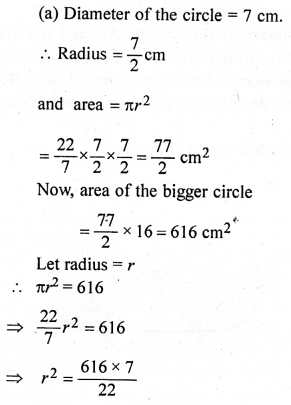

Question 18.
In the adjoining figure, A6CD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semicircle are drawn with AD and BC as diameters. Find the area of the shaded region. Take π = \(\frac { 22 }{ 7 }\).
Solution:

Question 19.
(a) In the figure (i) given below, ABCD is a square of side 14 cm and APD and BPC are semicircles. Find the area and the perimeter of the shaded region.
(b) In the figure (ii) given below, ABCD is a square of side 14 cm. Find the area of the shaded region.
(c) In the figure (iii) given below, the diameter of the semicircle is equal to 14 cm. Calculate the area of the shaded region. Take π = \(\frac { 22 }{ 7 }\).
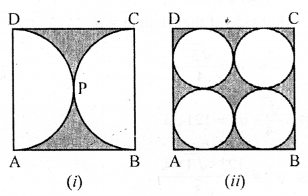
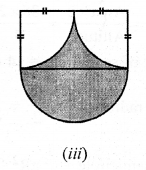
Solution:

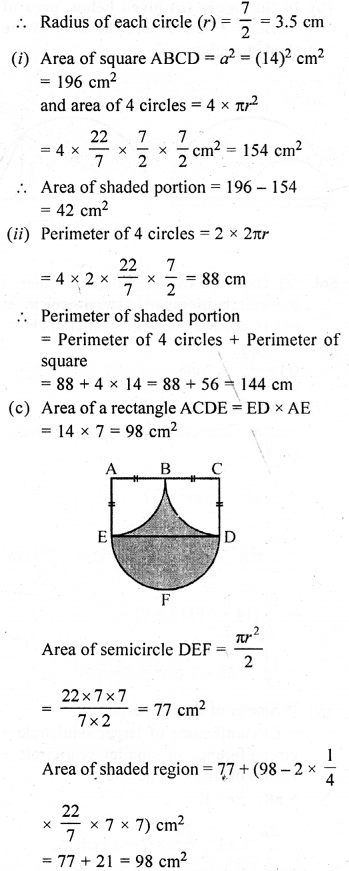
Question 20.
(a) Find the area and the perimeter of the shaded region in figure (i) given below. The dimensions are in centimetres.
(b) In the figure (ii) given below, area of ∆ABC = 35 cm2. Find the area of the shaded region.
Solution:


Question 21.
(a) In the figure (i) given below, AOBC is a quadrant of a circle of radius 10 m. Calculate the area of the shaded portion. Take π = 3.14 and give your answer correct to two significant figures.
(b) In the figure, (ii) given below, OAB is a quadrant of a cirlce. The radius OA = 3.5 cm and OD = 2 cm. Calculate the area of the shaded portion.
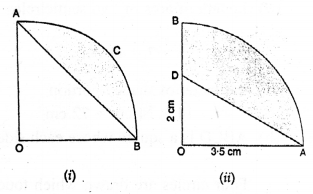
Solution:


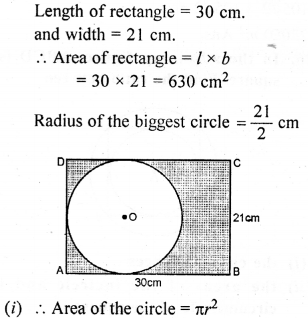
Question 22.
A student takes a rectangular piece of paper 30 cm long and 21 cm wide. Find the area of the biggest circle that can be cut out from the paper. Also find the area of the paper left after cutting out the circle. (Take π = \(\frac { 22 }{ 7 }\) )
Solution:

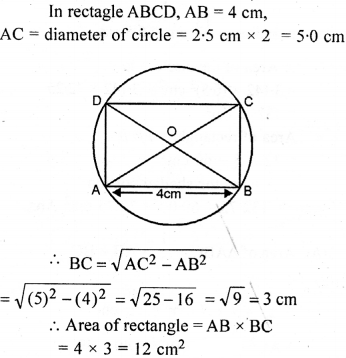
Question 23.
A rectangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle.
Solution:
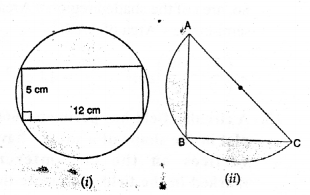
Question 24.
(a) In the figure (i) given below, calculate the area of the shaded region correct to two decimal places. (Take π = 3. 142).
(b) In the figure (ii) given below, ABC is an isosceles right angled triangle with ∠ABC = 90°. A semicircle is drawn with AC as diameter. If AB = BC = 7 cm, find the area of the shaded region. Take π = \(\frac { 22 }{ 7 }\) .
Solution:

Question 25.
A circular field has perimeter 660 m. A plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square field.
Solution:

Question 26.
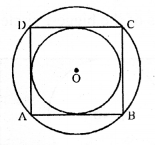
In the adjoining figure, ABCD is a square. Find the ratio between
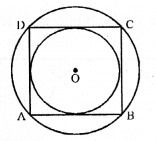
(i) the circumferences
(ii) the areas of the incircle and the circumcircle of the square.
Solution:

Question 27.
(a) The figure (i) given below shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end.
PQ = 200 m ; PT = 70 m.
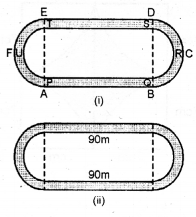
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track.
(b) In the figure (ii) given below, the inside perimeter of a practice running track with semi-circular ends and straight parallel sides is 312 m. The length of the straight portion of the track is 90 m. If the track has a uniform width of 2 m throughout, find its area.
Solution:


Question 28.
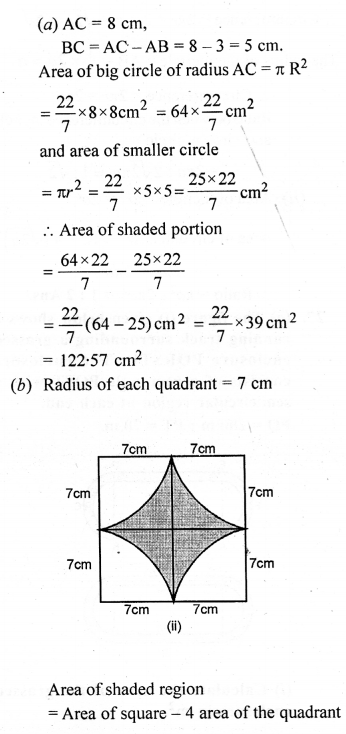
(a) In the figure (i) given below, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.
(b) The quadrants shown in the figure (ii) given below are each of radius 7 cm. Calculate the area of the shaded portion.
Solution:
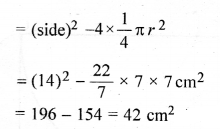
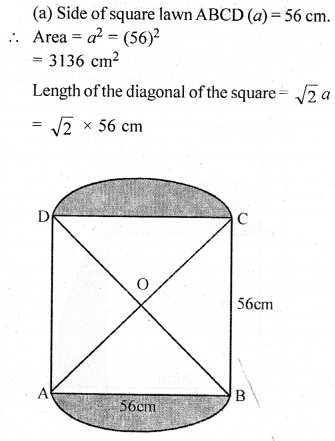
Question 29.
(a) In the figure (i) given below, two circular flower beds have been shown on the two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
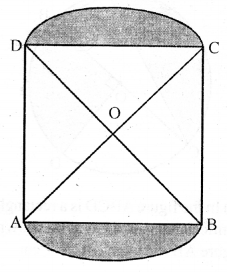
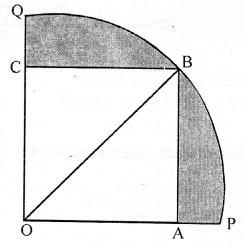
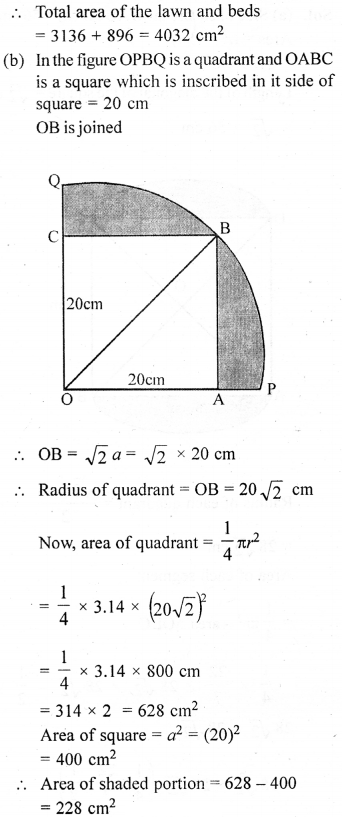
(b) In the figure (ii) given below, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
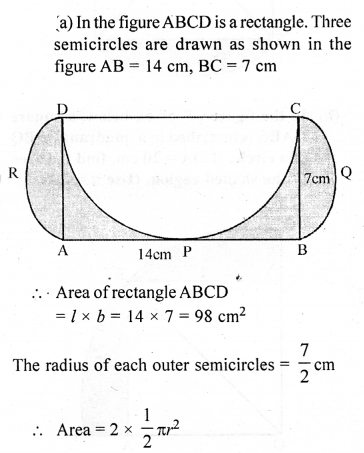
Solution:

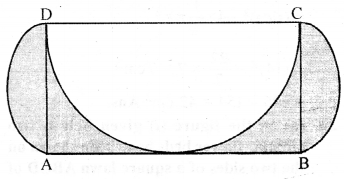
Question 30.
(a) In the figure (i) given below, ABCD is a rectangle, AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of the shaded portion.
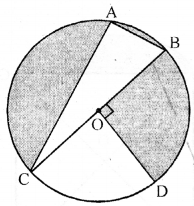
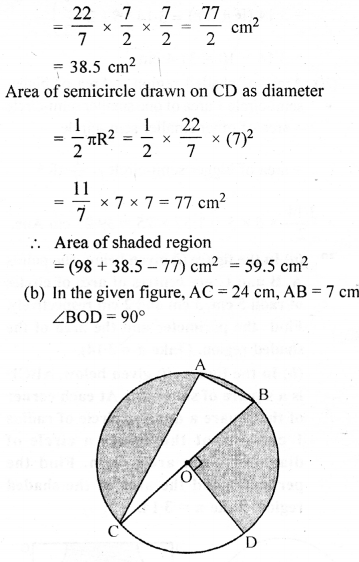
(b) In the figure (ii) given below, O is the centre of a circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (Use π = 3.14).
Solution:


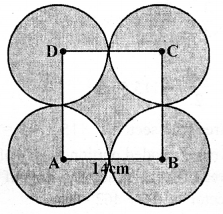
Question 31.
(a) In the figure given below ABCD is a square of side 14 cm. A, B, C and D are centres of the equal circle which touch externally in pairs. Find the area of the shaded region.
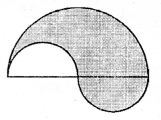
(b) In the figure (ii) given below, the boundary of the shaded region in the given diagram consists of three semi circular arcs, the smaller being equal. If the diameter of the larger one is 10 cm, calculate.
(i) the length of the boundary.
(ii) the area of the shaded region. (Take π to be 3.14)
Solution:


Question 32.
(a) In the figure (i) given below, the points A, B and C are centres of arcs of circles of radii 5 cm, 3 cni and 2 cm respectively. Find the perimeter and the area of the shaded region. (Take π = 3.14).
(b) In the figure (ii) given below, ABCD is a square of side 4 cm. At each corner of the square a quarter circle of radius 1 cm, and at the centre a circle of diameter 2 cm are drawn. Find the perimeter and the area of the shaded region. Take π = 3.14.
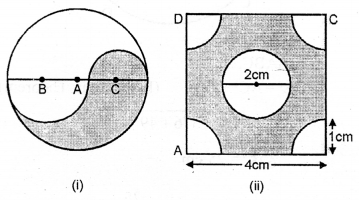
Solution:


Question 33.
(a) In the figure given below, ABCD is a rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle. (Take π = 22/7)
(b) The figure (ii) given below shows a kite, in which BCD is in the shape of a quadrant of circle of radius 42 cm. ABCD is a square and ∆ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
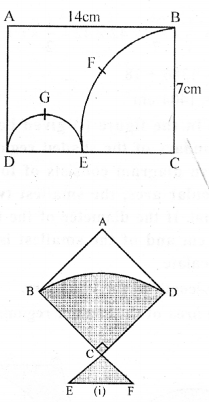
Solution:


Question 34.
(a) In the figure (i) given below, the boundary of the shaded region in the given diagram consists of four semi circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, calculate
(i) the length of the boundary.
(ii) the area of the shaded region.
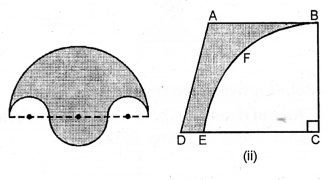
(b) In the figure (ii) given below, a piece of cardboard, in the shape of a trapezium ABCD, and AB || DC and ∠BCD = 90°, quarter circle BFEC is removed. Given AB = BC = 3.5 cm and DE = 2 cm. Calculate the area of the remaining piece of the cardboard.
Solution:
![]()



Question 35.
(a) In the figure (i) given below, ABC is a right angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semi-circle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
(b) In the figure (ii) given below, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of equal radius. Find the area of the shaded region correct upto 2 decimal places. (Take π = 3.142 and √3 = 1.732).
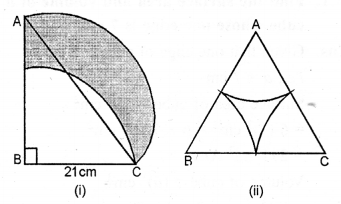
Solution:
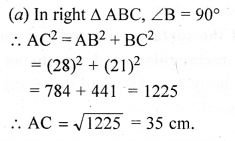

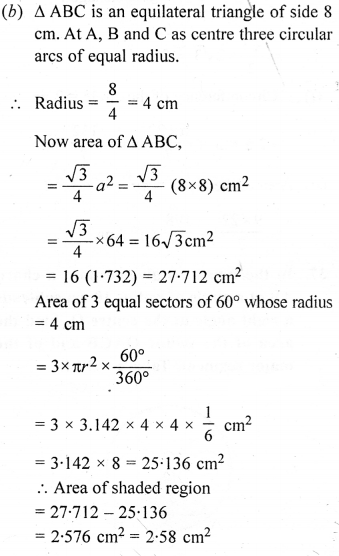
Question 36.
A circle is inscribed in a regular hexagon of side 2√3 cm. Find
(i) the circumference of the inscribed circle
(ii) the area of the inscribed circle
Solution:
ABCDEF is a regular hexagon of side 2√3 cm. and a circle is inscribed in it with centre O.
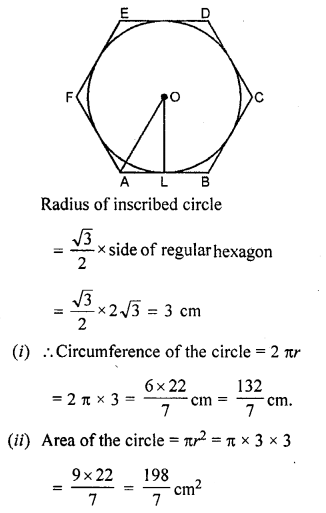
Question 37.
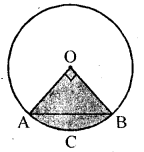
In the figure (i) given below, a chord AB of a circle of radius 10 cm subtends a right angle at the centre O. Find the area of the sector OACB and of the major segment. Take π = 3.14.
Solution:

EXERCISE 16.4
Question 1.
Find the surface area and volume of a cube whose one edge is 7 cm.
Solution:
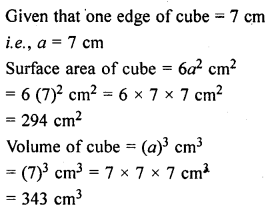
Question 2.
Find the surface area and the volume of a rectangular solid measuring 5 m by 4 m by 3 m. Also find the length of a diagonal.
Solution:

Question 3.
The length and breadth of a rectangular solid are respectively 25 cm and 20 cm. If the volume is 7000 cm3, find its height.
Solution:

Question 4.
A class room is 10 m long, 6 m broad and 4 m high. How many students can it accommodate if one student needs 1.5 m2 of floor area ? How many cubic metres of air will each student have ?
Solution:


Question 5.
(a) The volume of a cuboid is 1440 cm3. Its height is 10 cm and the cross-section is a square. Find the side of the square.
(b) The perimeter of one face of a cube is 20 cm. Find the surface area and the volume of the cube.
Solution:

Question 6.
Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden box covered with coloured papers with pictures of Santa Claus. She must know the exact quantity of paper to buy for this purpose. If the box has length 80 cm, breadth 40 cm and height 20 cm respectively, then how many square sheets of paper of side 40 cm would she require ?
Solution:

Question 7.
The volume of a cuboid is 3600 cm3 and its height is 12 cm. The cross-section is a rectangle whose length and breadth are in the ratio 4 :3. Find the perimeter of the cross-section.
Solution:

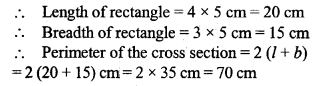
Question 8.
The volume of a cube is 729 cm3. Find its surface area and the length of a diagonal.
Solution:

Question 9.
The length of the longest rod which can be kept inside a rectangular box is 17 cm. If the inner length and breadth of the box are 12 cm and 8 cm respectively, find its inner height.
Solution:

Question 10.
A closed rectangular box has inner dimensions 90 cm by 80 cm by 70 cm. Calculate its capacity and the area of tin-foil needed to line its inner surface.
Solution:


Question 11.
The internal measurements of a box are 20 cm long, 16 cm wide and 24 cm high. How many 4 cm cubes could be put into the box ?
Solution:

Question 12.
The internal measurements of a box are 10 cm long, 8 cm wide and 7 cm high. How many cubes of side 2 cm can be put into the box ?
Solution:

Question 13.
A certain quantity of wood costs Rs. 250 per m3. A solid cubical block of such wood is bought for Rs. 182.25. Calculate the volume of the block and use the method of factors to find the length of one edge of the block.
Solution:

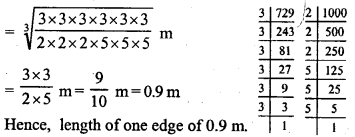
Question 14.
A cube of 11 cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of the base of the vessel are 15 cm x 12 cm, find the rise in the water level in centimetres correct to 2 decimal places, assuming that no water over flows.
Solution:

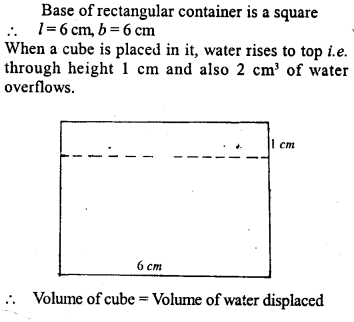
Question 15.
A rectangular container, whose base is a square of side 6 cm, stands on a horizontal table and holds water upto 1 cm from the top. When a cube is placed in the water and is completely submerged, the water rises to the top and 2 cm3 of water over flows.. Calculate the volume of the cube.
Solution:
![]()
Question 16.
(a) Two cubes, each with 12 cm edge, are joined end to end. Find the surface area of the resulting cuboid,
(b) A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube ? Also, find the ratio between the surface area of the original cube and the sum of the surface areas of the new cubes.
Solution:
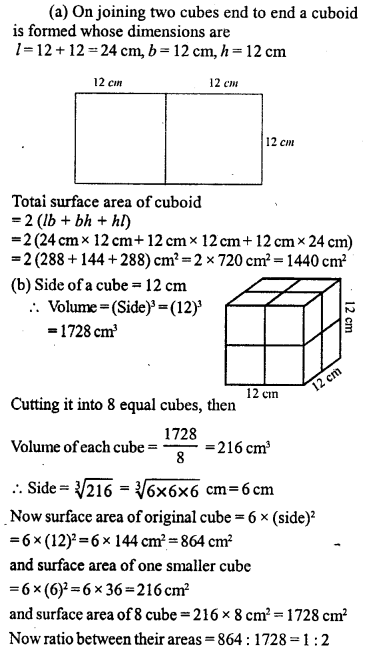
Question 17.
A cube of a metal of 6 cm edge is melted and cast into a cuboid whose base is 9 cm x g cm. Find the height of the cuboid.
Solution:

Question 18.
The area of a playground is 4800 m2. Find the cost of covering it with gravel 1 cm deep, if the gravel costs Rs. 260 per cubic metre.
Solution:

Question 19.
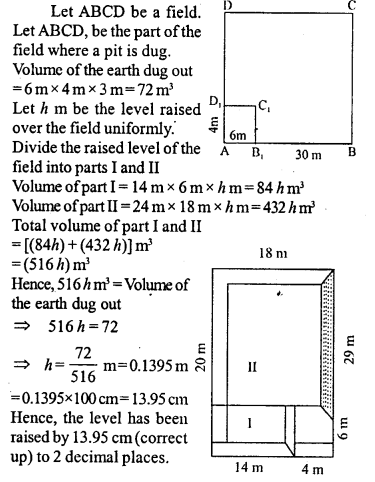
A field is 30 m long and 18 m broad. A pit 6 m long, 4m wide and 3 m deep is dug out from the middle of the field and the earth removed is evenly spread over the remaining area of the field. Find the rise in the level of the remaining part of the field in centimetres correct to two decimal places.
Solution:
Question 20.
A rectangular plot is 24 m long and 20 m wide. A cubical pit of edge 4 m is dug at each of the four corners of the field and the soil removed is evenly spread over the remaining part of the plot. By what height does the remaining plot get raised?
Solution:

Question 21.
The inner dimensions of a closed wooden box are 2 m, 1.2 m and .75 m. The thickness of the wood is 2.5 cm. Find the cost of wood required to make the box if 1 m3 of wood costs Rs. 5400.
Solution:

Question 22.
A cubical wooden box of internal edge 1 mis made of 5 cm thick wood. The box is open at the top. If the wood costs Rs. 9600 per cubic metre, find the cost of the wood required to make the box.
Solution:

Question 23.
A square brass plate of side x cm is 1mm thick and weighs 4725 g. If one. cc of brass weighs 8.4 gm, find the value of x.
Solution:

Question 24.
Three cubes whose edges are x cm, 8 cm and 10 cm respectively are melted and recast into a single cube of edge 12 cm. Find x.
Solution:
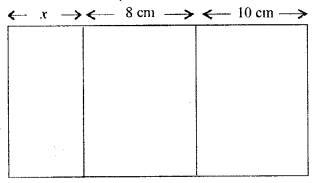

Question 25.
The area of cross-section of a pipe is 3.5 cm2 and water is flowing out of pipe at the rate of 40 cm/s. How much water is delivered by the pipe in one minute ?
Solution:

Question 26.
(a) The figure (i) given below shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in cm and all angles in the figure are right angles.
(b) The figure (ii) given below shows the cross section of a concrete wall to be constructed. It is 2 m wide at the top, 3.5 m wide at the bottom and its
height is 6 m, and its length is 400 m. Calculate (i) The cross-sectional area, and (ii) volume of concrete in the wall.
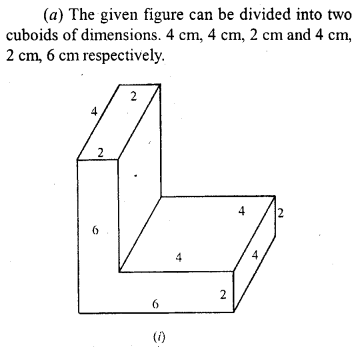
(c) The figure (iii) given below show the cross section of a swimming pool 10 m broad, 2 m deep at one end and 3 m deep at the other end. Calculate the volume of water it will hold when full, given that its length is 40 m.
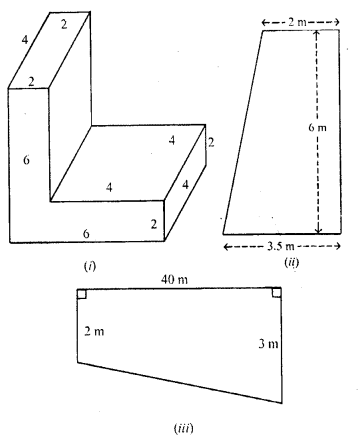
Solution:

Question 27.
A swimming pool is 50 metres long and 15 metres wide. Its shallow and deep ends arc 1\(\frac { 1 }{ 2 }\) metres and 14\(\frac { 1 }{ 2 }\) metres deep respectively. If the bottom of the pool slopes uniformly, find the amount of water required to fill the pool.
Solution:

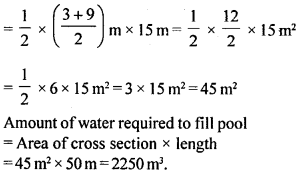
Multiple Choice Questions
Choose the correct answer from the given four options (1 to 24):
Question 1.
Area of a triangle is 30 cm2. If its base is 10 cm, then its height is
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
Solution:

Question 2.
If the perimeter of a square is 80 cm, then its area is
(a) 800 cm2
(b) 600 cm2
(c) 400 cm2
(d) 200 cm2
Solution:

Question 3.
Area of a parallelogram is 48 cm2. If its height is 6 cm then its base is
(a) 8 cm
(b) 4 cm
(c) 16 cm
(d) None of these
Solution:

Question 4.
If d is the diameter of a circle, then its area is
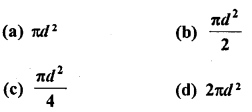
Solution:
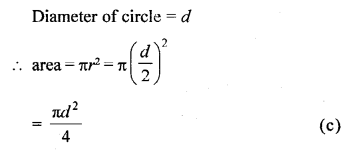
Question 5.
If the area of a trapezium is 64 cm2 and the distance between parallel sides is 8 cm, then sum of its parallel sides is
(a) 8 cm
(b) 4 cm
(c) 32 cm
(d) 16 cm
Solution:

Question 6.
Area of a rhombus whose diagonals are 8 cm and 6 cm is
(a) 48 cm2
(b) 24 cm2
(c) 12 cm2
(d) 96 cm2
Solution:
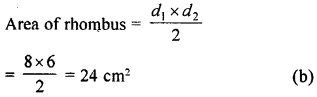
Question 7.
If the lengths of diagonals of a rhombus is doubled, then area of rhombus will be
(a) doubled
(b) tripled
(c) four times
(d) remains same
Solution:
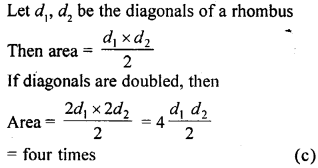
Question 8.
If the length of a diagonal of a quadrilateral is 10 cm and lengths of the perpendiculars on it from opposite vertices are 4 cm and 6 cm, then area of quadrilateral is
(a) 100 cm2
(b) 200 cm2
(c) 50 cm2
(d) None of these
Solution:
![]()

Question 9.
Area of a rhombus is 90 cm2. If the length of one diagonal is 10 cm then the length of other diagonal is
(a) 18 cm
(b) 9 cm
(c) 36 cm
(d) 4.5 cm
Solution:
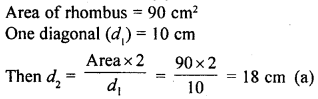
Question 10.
In the given figure, OACB is a quadrant of a circle of radius 7 cm. The perimeter of the quadrant is
(a) 11 cm
(b) 18 cm
(c) 25 cm
(d) 36 cm
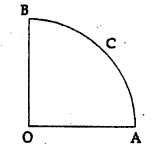
Solution:

Question 11.
In the given figure, OABC is a square of side 7 cm. OAC is a quadrant of a circle with O as centre. The area of the shaded region is
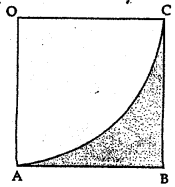
(a) 10.5 cm2
(b) 38.5 cm
(c) 49 cm2
(d) 11.5 cm2
Solution:

Question 12.
The given figure shows a rectangle and a semicircle. The perimeter of the shaded region is
(a) 70 cm
(b) 56 cm
(c) 78 cm
(d) 46 cm
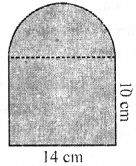
Solution:
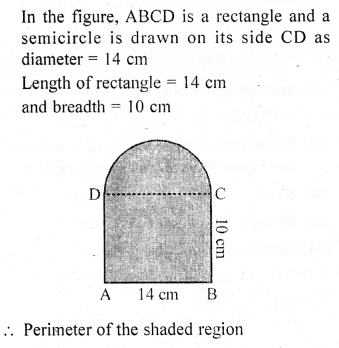
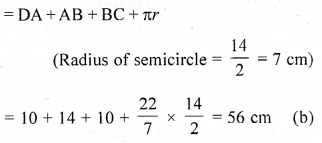
Question 13.
The area of the shaded region shown in Q. 12 (above is
(a) 140 cm2
(b) 77 cm2
(c) 294 cm2
(d) 217 cm2
Solution:

Question 14.
In the given figure, the boundary of the shaded region consists of semicircular arcs. The area of the shaded region is equal to
(a) 616 cm2
(b) 385 cm2
(c) 231 cm2
(d) 308 cm2
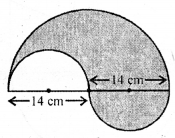
Solution:
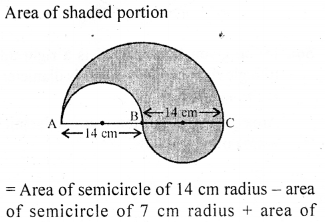

Question 15.
The perimeter of the shaded region shown in Q. 14 (above) is
(a) 44 cm
(b) 88 cm
(c) 66 cm
(d) 132 cm
Solution:

Question 16.
In the given figure, ABC is a right angled triangle at B. A semicircle is drawn on AB as diameter. If AB = 12 cm and BC = 5 cm, then the area of the shaded region is
(a) (60 + 18π) cm2
(b) (30 + 36π) cm2
(c) (30+18π) cm2
(d) (30 + 9π) cm2
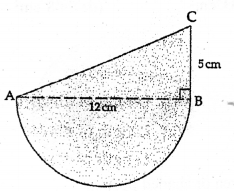
Solution:

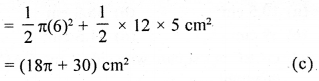
Question 17.
The perimeter of the shaded region shown in Q. 16 (above) is
(a) (30 + 6π) cm
(b) (30 + 12π) cm
(c) (18 + 12π) cm
(d) (18 + 6π) cm
Solution:

Question 18.
If the volume of a cube is 729 m3, then its surface area is
(a) 486 cm2
(b) 324 cm2
(c) 162 cm2
(d) None of these
Solution:
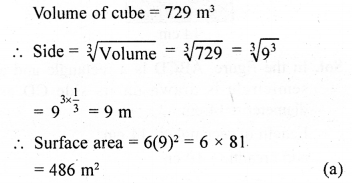
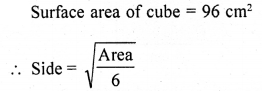
Question 19.
If the total surface area of a cube is 96 cm2, then the volume of the cube is
(a) 8 cm3
(b) 512 cm3
(c) 64 cm3
(d) 27 cm3
Solution:
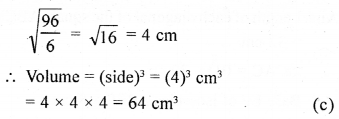
Question 20.
The length of the longest pole that can be put in a room of dimensions (10 m x 10 m x 5 m) is
(a) 15 m
(b) 16 m
(c) 10 m
(d) 12 m
Solution:
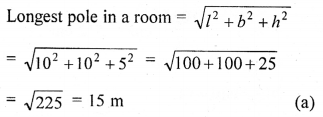
Question 21.
The lateral surface area of a cube is 256 m2. The volume of the cube is
(a) 512 m3
(b) 64 m3
(c) 216 m3
(d) 256 m3
Solution:

Question 22.
If the perimeter of one face of a cube is 40 cm, then the sum of lengths of its edge is
(a) 80 cm
(b) 120 cm
(c) 160 cm
(d) 240 cm
Solution:

Question 23.
A cuboid container has the capacity to hold 50 small boxes. If all the dimensions of the container are doubled, then it can hold (small boxes of same size)
(a) 100 boxes
(b) 200 boxes
(c) 400 boxes
(d) 800 boxes
Solution:

Question 24.
The number of planks of dimensions (4 m x 50 cm x 20 cm) that can be stored in a pit which is 16 m long, 12 m wide and 4 m deep is
(a) 1900
(b) 1920
(c) 1800
(d) 1840
Solution:

Chapter Test
Question 1.
(a) Calculate the area of the shaded region.
(b) If the sides of a square are lengthened by 3 cm, the area becomes 121 cm2. Find the perimeter of the original square.
Solution:

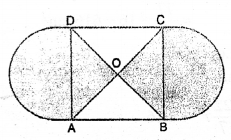
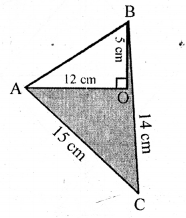
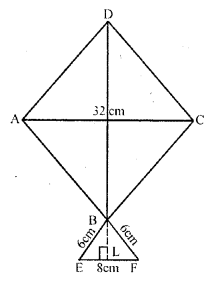
Question P.Q.
The given figure shows a kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and side 6cm each. How much paper is used in making the kite ? Ignore the wastage of the paper is making the kite.
Solution:

Question 2.
(a) Find the area enclosed by the figure (i) given below. All measurements are in centimetres:
(b) Find the area of the quadrilateral ABCD shown in figure (ii) given below. All measurements are in centimetres.
(c) Calculate the area of the shaded region shown in figure (iii) given below. All measurements are in metres.
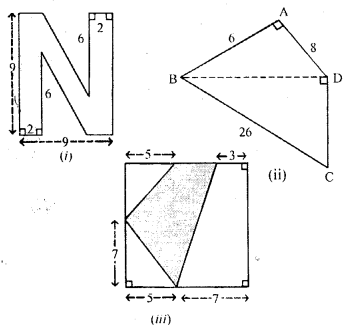
Solution:
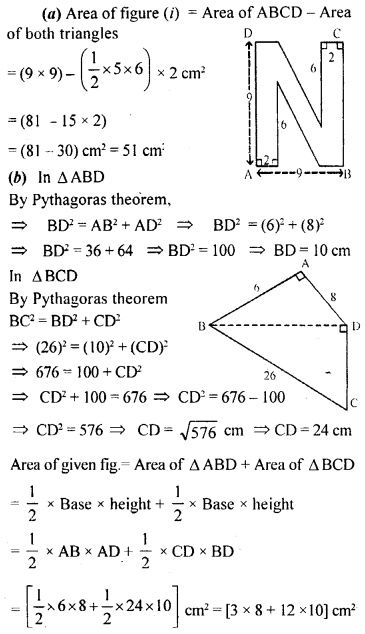
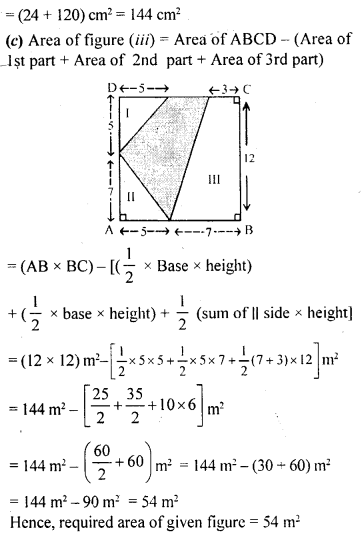
Question 3.
Asifa cut an aeroplane from a coloured chart paper (as shown in the adjoining figure). Find the total area of the chart paper used, correct to 1 decimal place.
Solution:
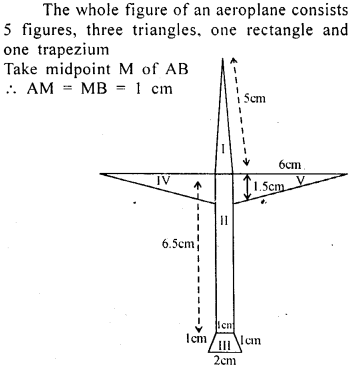
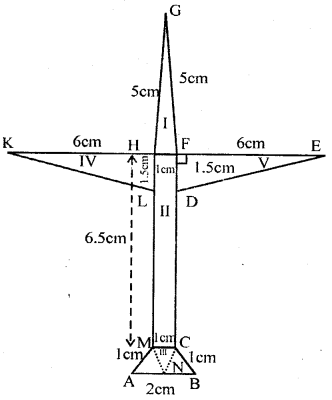


Question 4.
If the area of a circle is 78.5 cm2, find its circumference. (Take π = 3.14)
Solution:

Question 5.
From a square cardboard, a circle of biggest area was cut out. If the area of the circle is 154 cm2, calculate the original area of the cardboard.
Solution:
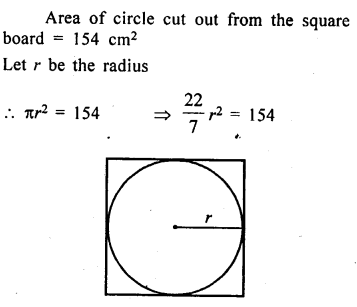
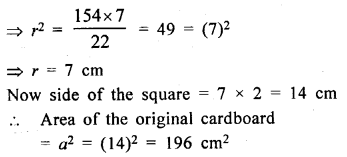
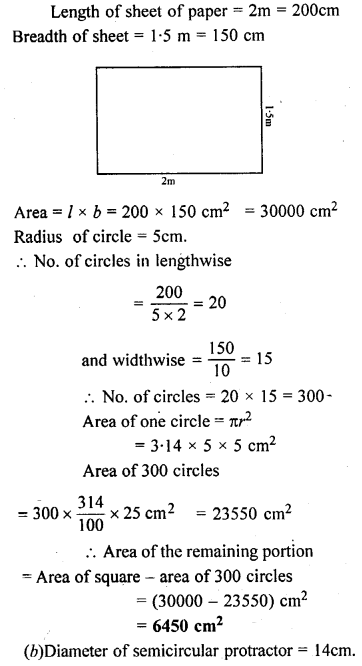
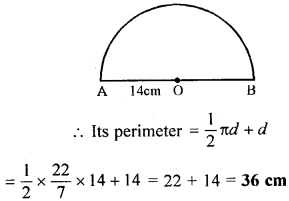
Question 6.
(a) From a sheet of paper of dimensions = 2m x 1.5m, how many circles can you cut of radius 5cm. Also find the area of the paper wasted. Take π = 3.14.
(b) If the diameter of a semicircular protractor is 14cm, then find its perimeter.
Solution:
Question 7.
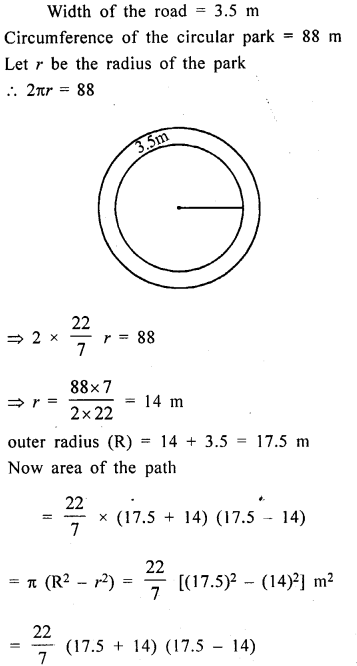
A road 3.5 m wide surrounds a circular park whose circumference is 88 m. Find the cost of paving the road at the rate of Rs. 60 per square metre.
Solution:

Question 8.
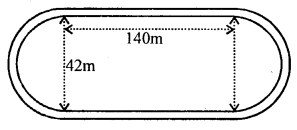
The adjoining sketch shows a running tract 3.5 m wide all around which consists of two straight paths and two semicircular rings. Find the area of the track.
Solution:

Question 9.
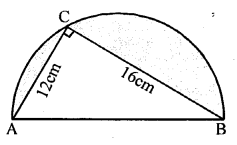
In the adjoining figure, O is the centre of a circular arc and AOB is a line segment.Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
Solution:

Question 10.
(a) In the figure (1) given below, the radius is 3.5 cm. Find the perimeter of the quarter of the circle.
(b) In the figure (ii) given below, there are five squares each of side 2 cm.
(i) Find the radius of the circle.
(ii) Find the area of the shaded region. (Take π= 3.14).
Solution:
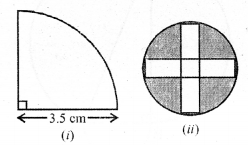
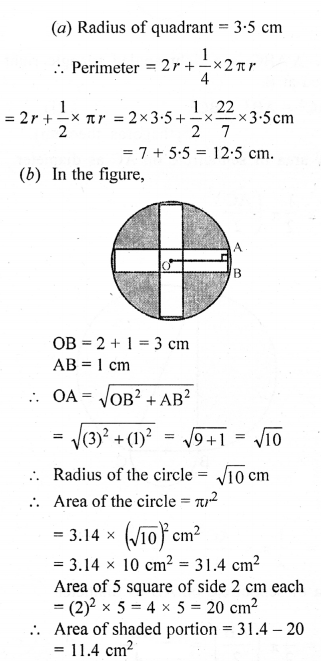
Question 11.
(a) In the figure (i) given below, a piece of cardboard in the shape of a quadrant of a circle of radius 7 cm is bounded by perpendicular radii OX and OY. Points A and B lie on OX and OY respectively such that OA = 3 cm and OB = 4 cm. The triangular part OAB is removed. Calculate the area and the perimeter of the remaining piece.

(b) In the figure (ii) given below, ABCD is a square. Points A, B, C and D are centres of quadrants of circles of the same radius. If the area of the shaded portion is 21\(\frac { 3 }{ 7 }\)
cm2, find the radius of the quadrants. Take π = \(\frac { 22 }{ 7 }\).
Solution:

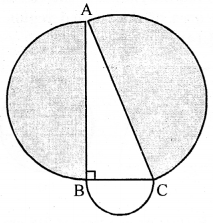
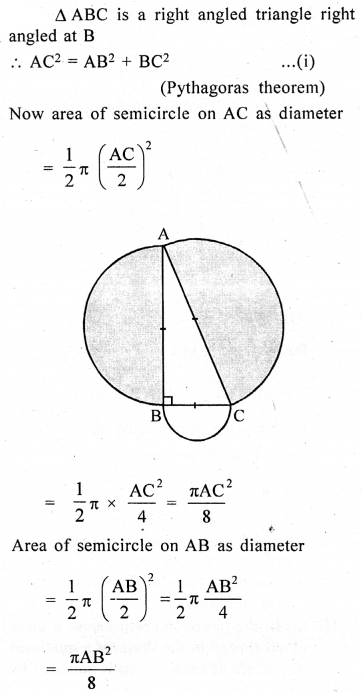
Question 12.
In the adjoining figure, ABC is a right angled triangle right angled at B. Semicircle are drawn on AB, BC and CA as diameter. Show that the sum of areas of semi circles drawn on AB and BC as diameter is equal to the area of the semicircle drawn on CA as diameter.
Solution:

Question 13.
The length of minute hand of a clock is 14 cm. Find the area swept by the minute hand in 15 minutes.
Solution:

Question 14.
Find the radius of a circle if a 90° arc has a length of 3.5 n cm. Hence, find the area of sector formed by this arc.
Solution:

Question 15.
A cube whose each edge is 28 cm long has a circle of maximum radius on each of its face painted red. Find the total area of the unpainted surface of the cube.
Solution:

Question 16.
Can a pole 6.5 m long fit into the body of a truck with internal dimensions of 3.5m, 3 m and 4m?
Solution:

Question 17.
A car has a petrol tank 40 cm long, 28 cm wide and 25 cm deep. If the fuel consumption of the car averages 13.5 km per litre, how far can the car travel with a full tank of petrol ?
Solution:


Question 18.
An aquarium took 96 minutes to completely fill with water. Water was filling the aquarium at a rate of 25 litres every 2 minutes. Given that the aquarium was 2 m long and 80 cm wide, compute the height of the aquarium.
Solution:

Question 19.
The lateral surface area of a cubiod is 224 cm2. Its height is 7 cm and the base is a square. Find :
(i) a side of the square, and
(ii) the volume of the cubiod.
Solution:

Question 20.
If the volume of a cube is V m3, its surface area is S m2 and the length of a diagonal is d metres, prove that 6√3 V = S d.
Solution:
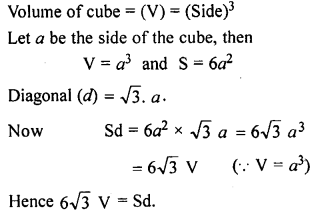
Question 21.
The adjoining figure shows a victory stand, each face is rectangular. All measurement are in centimetres. Find its volume and surface area (the bottom of the stand is open).
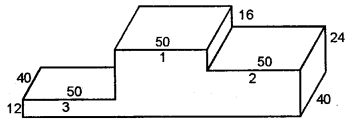
Solution:

Question 22.
The external dimensions of an open rectangular wooden box are 98 cm by 84 cm by 77 cm. If the wood is 2 cm thick all around, find :
(i) the capacity of the box
(ii) the volume of the wood used in making the box, and
(iii) the weight of the box in kilograms correct to one decimal place, given that 1 cm3 of wood weighs 0.8 gm.
Solution:


Question 23.
A cuboidal block of metal has dimensions 36 cm by 32 cm by 0.25 m. It is melted and recast into cubes with an edge of 4 cm.
(i) How many such cubes can be made ?
(ii) What is the cost of silver coating the surfaces of the cubes at the rate of Rs. 1.25 per square centimetre ?
Solution:


Question 24.
Three cubes of silver with edges 3 cm, 4 cm and 5 cm are melted and recast into a single cube. Find the cost of coating the surface of the new cube with gold at the rate of Rs. 3.50 per square centimetre.
Solution: