ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 15 Circle
EXERCISE 15.1
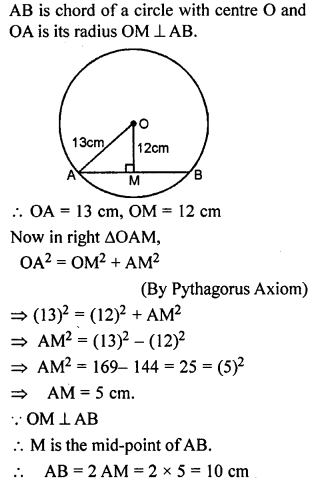
Question 1.
Calculate the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13 cm.
Solution:
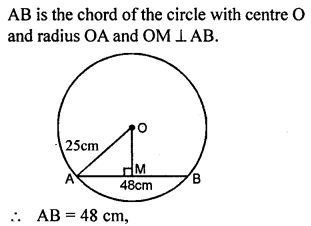
Question 2.
A chord of length 48 cm is drawn in a circle of radius 25 cm. Calculate its distance from the centre of the circle.
Solution:

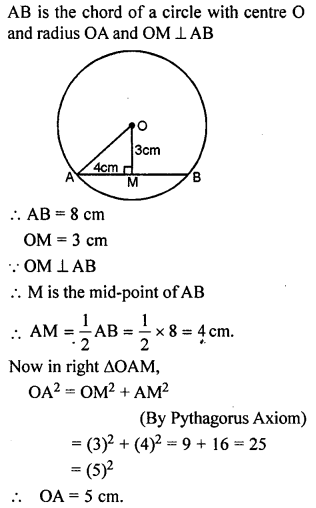
Question 3.
A chord of length 8 cm is at a distance of 3 cm from the centre of the circle. Calculate the radius of the circle.
Solution:
Question 4.
Calculate the length of the chord which is at a distance of 6 cm from the centre of a circle of diameter 20 cm.
Solution:
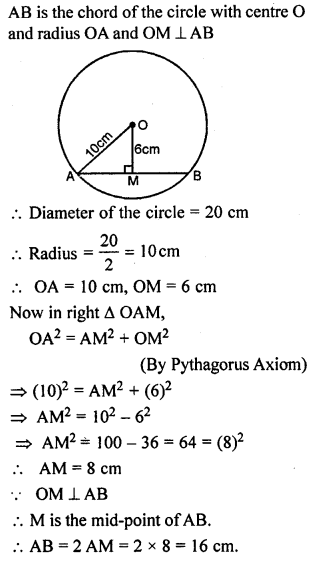
Question 5.
A chord of length 16 cm is at a distance of 6 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 8 cm from the centre.
Solution:
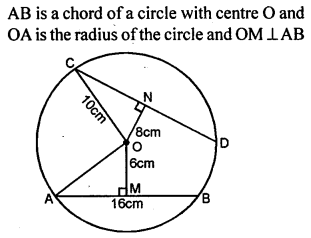

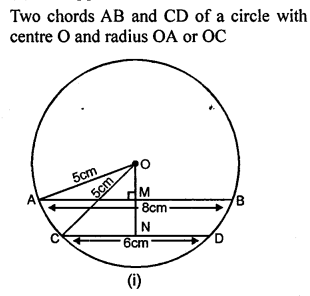
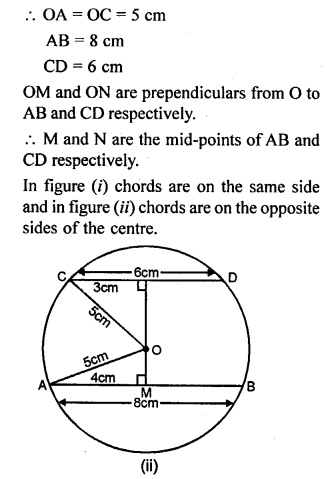
Question 6.
In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on :
(i) the same side of the centre.
(ii) the opposite sides of the centre.
Solution:

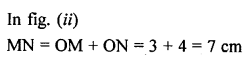
Question 7.
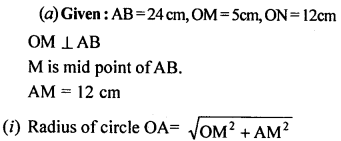
(a) In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle, OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the:
(i) radius of the circle.
(ii) length of chord CD.
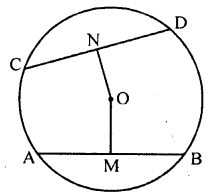
(b) In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.
Solution:
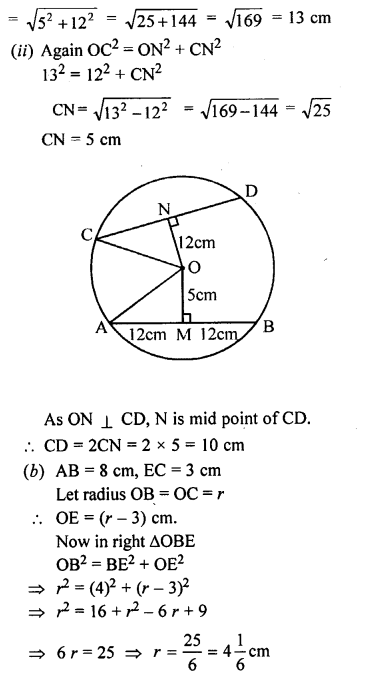
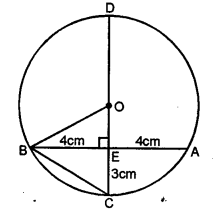
Question 8.
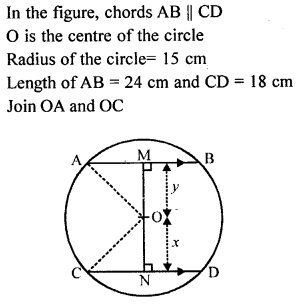
In the adjoining figure, AB and CD ate two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
Solution:

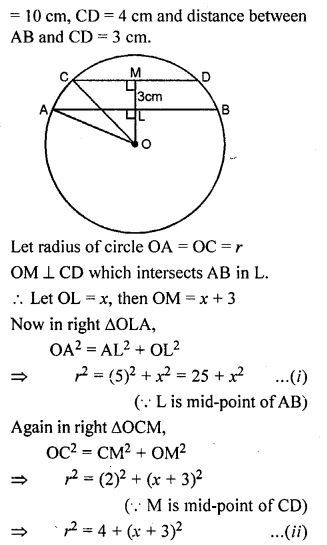
Question 9.
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.
Solution:
![]()

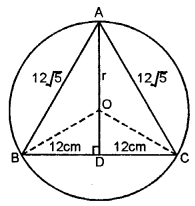
Question 10.
ABC is an isosceles triangle inscribed in a circle. If AB = AC = 12√5 cm and BC = 24 cm, find the radius of the circle.
Solution:
![]()

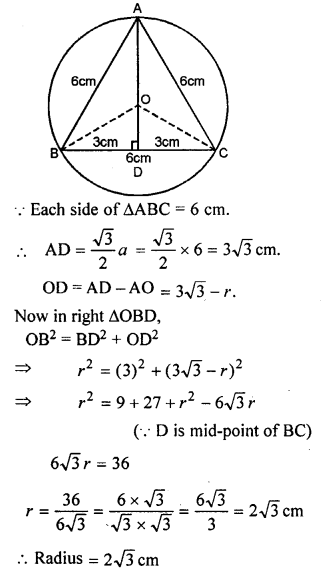
Question 11.
An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.
Solution:

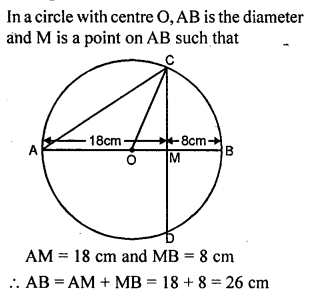
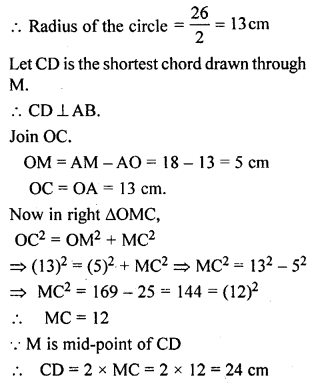
Question 12.
AB is a diameter of a circle. M is a point in AB such that AM = 18 cm and MB = 8 cm. Find the length of the shortest chord through M.
Solution:
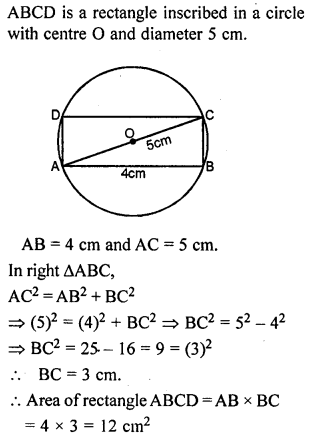
Question 13.
A rectangle with one side of length 4 cm is inscribed in a circle of diameter 5 cm. Find the area of the rectangle.
Solution:
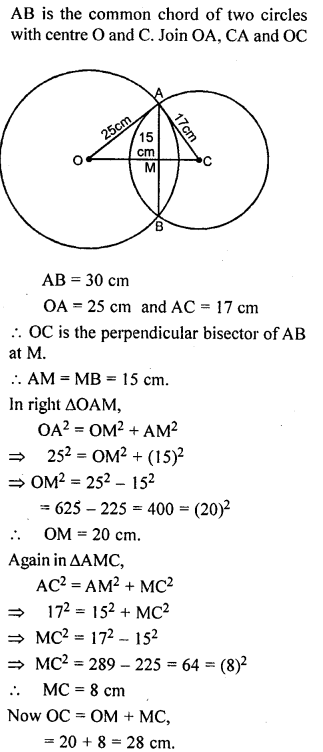
Question 14.
The length of the common chord of two intersecting circles is 30 cm. If the radii of the two circles are 25 cm and 17 cm, find the distance between their centres.
Solution:
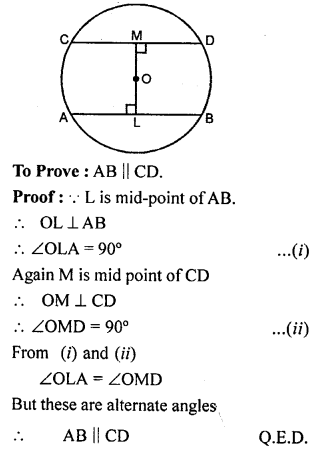
Question 15.
The line joining the mid-points of two chords of a circle passes through its centre. Prove that the chords are parallel.
Solution:

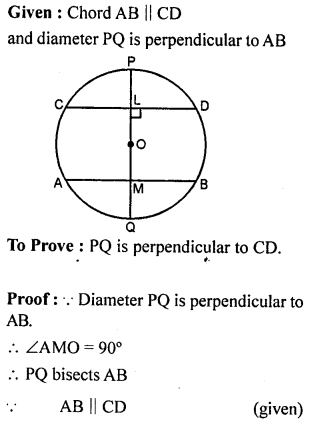
Question 16.
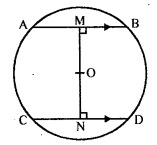
If a diameter of a circle is perpendicular to one of two parallel chords of the circle, prove that it is perpendicular to the other and bisects it.
Solution:

Question 17.
In an equilateral triangle, prove that the centroid and the circumcentre of the triangle coincide.
Solution:

Question 18.
(a) In the figure (i) given below, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA = 2 OD.
(b) In the figure (ii) given below, O is the centre of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, Prove that PB = QC.
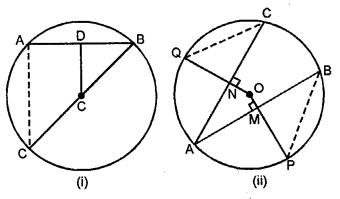
Solution:
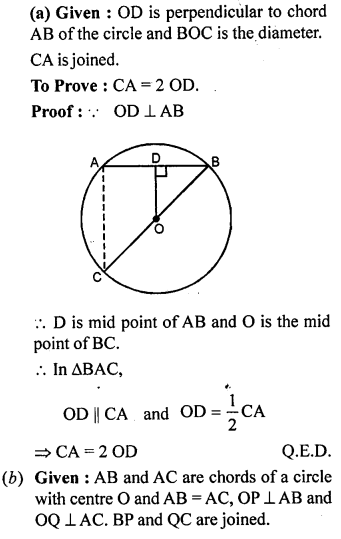

Question 19.
(a) In the figure (i) given below, a line l intersects two concentric circles at the points A, B, C and D. Prove that AB = CD.
(b) In the figure (it) given below, chords AB and CD of a circle with centre O intersect at E. If OE bisects ∠AED, Prove that AB = CD.

Solution:
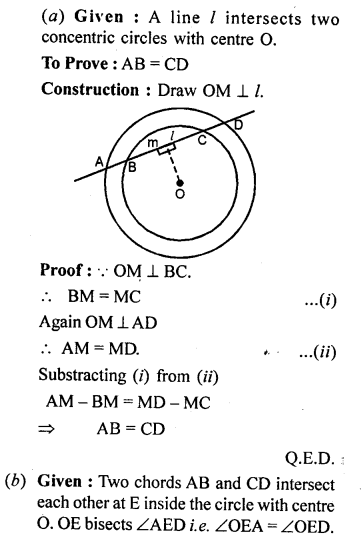
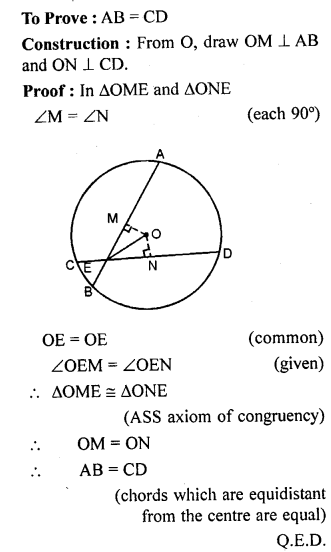
Question 20.
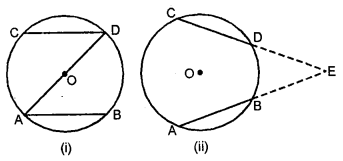
(a) In the figure (i) given below, AD is a diameter of a circle with centre O.
If AB || CD, prove that AB = CD.
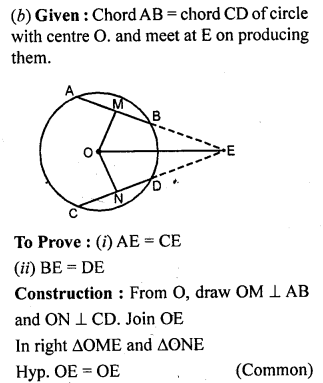
(b) In the figure (ii) given below, AB and CD are equal chords of a circle with centre O. If AB and CD meet at E (outside the circle) Prove that :
(i) AE = CE (ii) BE = DE.
Solution:
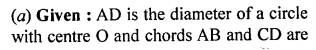


EXERCISE 15.2
Question 1.
If arcs APB and CQD of a circle are congruent, then find the ratio of AB: CD.
Solution:

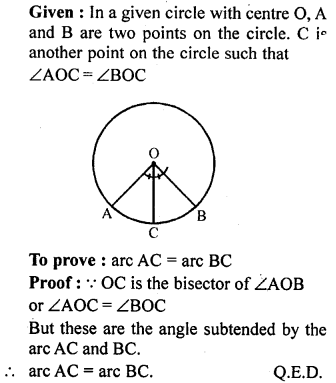
Question 2.
A and B are points on a circle with centre O. C is a point on the circle such that OC bisects ∠AOB, prove that OC bisects the arc AB.
Solution:
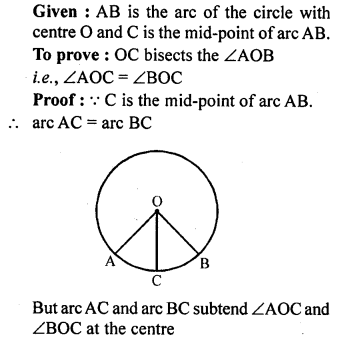
Question 3.
Prove that the angle subtended at the centre of a circle is bisected by the radius passing through the mid-point of the arc.
Solution:
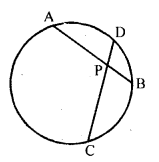
Question 4.
In the given figure, two chords AB and CD of a circle intersect at P. If AB = CD, prove that arc AD = arc CB.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (1 to 6) :
Question 1.
If P and Q are any two points on a circle, then the line segment PQ is called a
(a) radius of the circle
(b) diameter of the circle
(c) chord of the circle
(d) secant of the circle
Solution:
chord of the circle (c)
Question 2.
If P is a point in the interior of a circle with centre O and radius r, then
(a) OP = r
(b) OP > r
(c) OP ≥ r
(d) OP < r
Solution:
OP > r (b)
Question 3.
The circumference of a circle must be
(a) a positive real number
(b) a whole number
(c) a natural number
(d) an integer
Solution:
a positive real number (a)
Question 4.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm and AB = 30 cm, then the distance of AB from the centre of circle is
(a) 17 cm
(b) 15 cm
(c) 4 cm
(d) 8 cm
Solution:
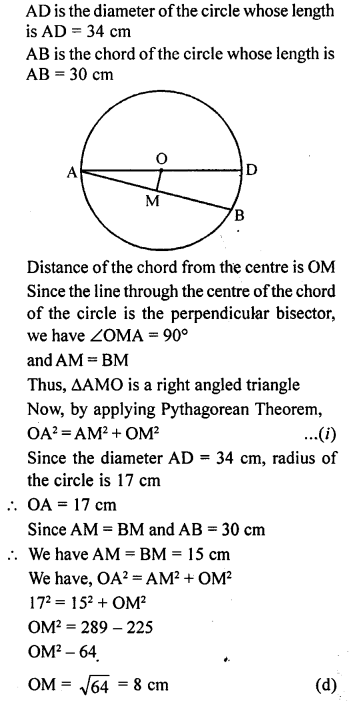
Question 5.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Solution:
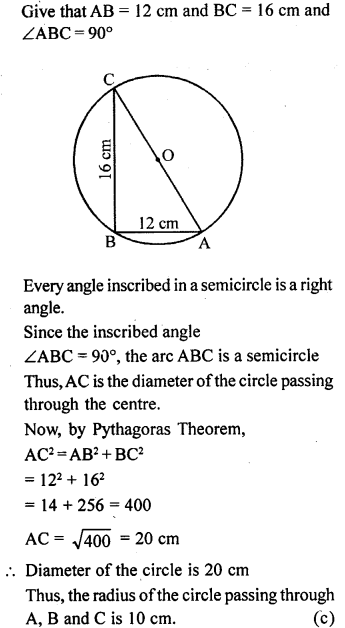
Question 6.
In the given figure, O is the centre of the circle. If OA = 5 cm, AB = 8 cm and OD ⊥ AB, then length of CD is equal to
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm
Solution:
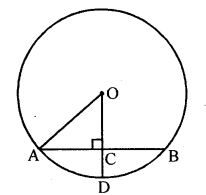
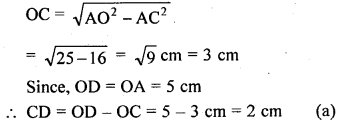
Chapter Test
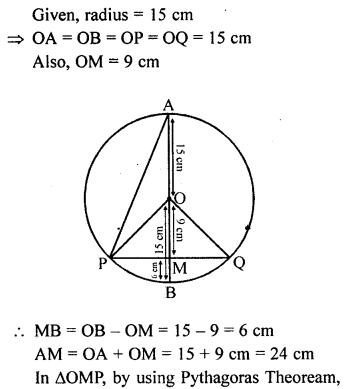
Question 1.
In the given figure, a chord PQ of a circle with centre O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of :
(i) PQ
(ii) AP
(iii) BP
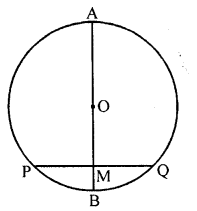
Solution:

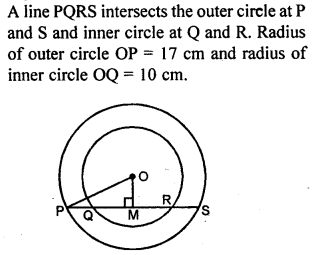
Question 2.
The radii of two concentric circles are 17 cm and 10 cm ; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.
Solution:

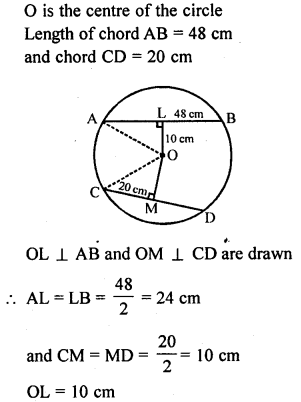
Question 3.
A chord of length 48 cm is at a distance of 10 cm from the centre of a circle. If another chord of length 20 cm is drawn in the same circle, find its distance from the centre of the circle.
Solution:

Question 4.
(a) In the figure (i) given below, two circles with centres C, D intersect in points P, Q. If length of common chord is 6 cm and CP = 5 cm, DP = 4 cm, calculate the distance CD correct to two decimal places.

(b) In the figure (ii) given below, P is a point of intersection of two circles with centres C and D. If the st. line APB is parallel to CD, Prove that AB = 2 CD.
Solution:
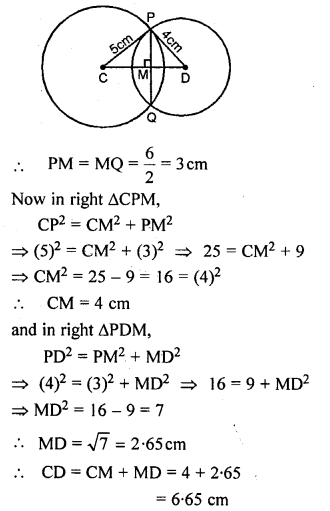
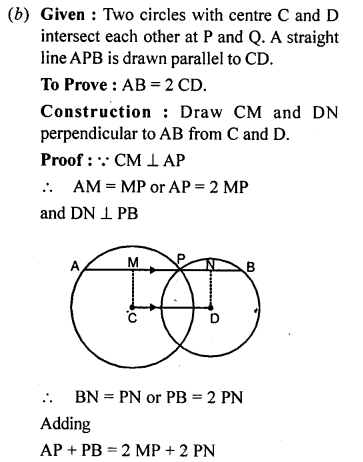
Question 5.
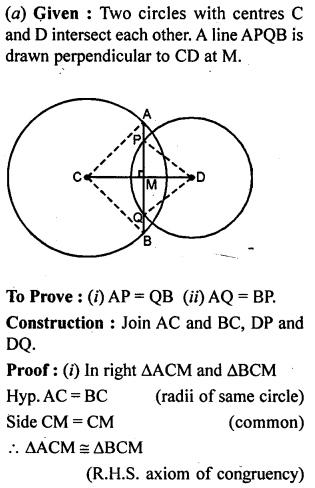
(a) In the figure (i) given below, C and D are centres of two intersecting circles. The line APQB is perpendicular to the line of centres CD.Provethat:
(i) AP=QB
(ii) AQ = BP.
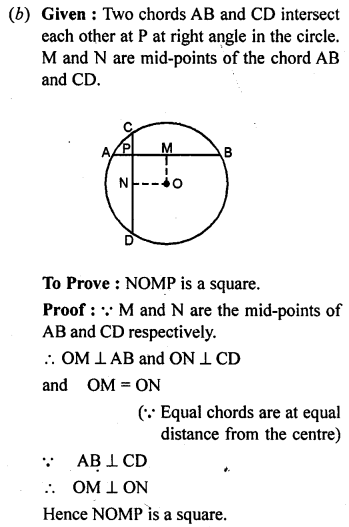
(b) In the figure (ii) given below, two equal chords AB and CD of a circle with centre O intersect at right angles at P. If M and N are mid-points of the chords AB and CD respectively, Prove that NOMP is a square.
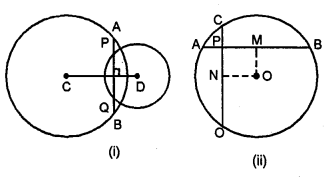
Solution:

Question 6.
In the given figure, AD is diameter of a circle. If the chord AB and AC are equidistant from its centre O, prove that AD bisects ∠BAC and ∠BDC.
Solution: