ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 14 Theorems on Area Chapter Test

ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 14 Theorems on Area Chapter Test

Question 1.
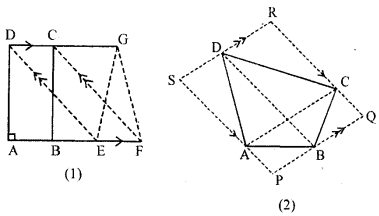
(a) In the figure (1) given below, ABCD is a rectangle (not drawn to scale ) with side AB = 4 cm and AD = 6 cm. Find :
(i) the area of parallelogram DEFC
(ii)area of ∆EFG
(b) In the figure (2) given below, PQRS is a parallelogram formed by drawing lines parallel to the diagonals of a quadrilateral ABCD through its corners. Prove that area of || gm PQRS = 2 × area of quad. ABCD.

Answer:
(a)Given. ABCD is a rectangle AB = 4 cm and AD = 6 cm.
D C cm and AD = 6 cm.
Required. (i) The area of || gm DEFC.
(ii) area of ∆ EFG
Answer:
(i) Since AB = 4cm and AD = 6 cm (given)

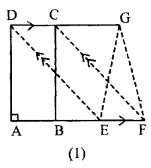
∴ Area of rectangle ABCD = AB × AD
= 4 cm × 6 cm = 24 cm²
Now, area of rectangle ABCD = area of || gm DEFC (∵ Both are on the same Base and between the same parallel lines)
⇒ Area of || gm DEFC = 24 cm²

(ii) Area of ∆EFG = \(\frac{1}{2}\) (area of || gm DEFC)
(∴ Both are on the same base and between the same parallel lines)
∴ Area of AEFG = \(\frac{1}{2}\)7 × 24 cm² =12 cm²

(b) Given. PQRS is a || gm formed by drawing lines parallel to the diagonals of quadrilateral ABCD through its comers.
To prove. Area of II gm PQRS = 2. area of quad. ABCD

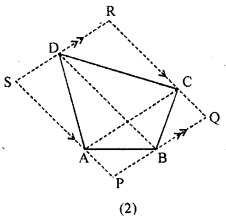
Proof. ar(∆ACD) = \(\frac{1}{2}\)ar(|| gm ACRS)
[∴ both are on same base AC and between the same || AC and SR ]
⇒ ar (|| gmACRS) = 2ar(∆ACD) …….(1)
Similarly,
ar ( ∆ ABC) = \(\frac{1}{2}\)ar (|| gm ∆APQC)
⇒ ar (|| gm APQC) = 2ar ( ∆ ABC) …..(2)
Adding (1) from (2),
ar (|| gm ACRS) + ar (|| gm APQC) = 2ar(∆ACD) + 2ar (∆ABC)
⇒ (|| gm PQRS) = 2[ar (∆ ACD) + ar ( ∆ ABC)]
⇒ ar (|| gm PQRS) = 2ar (quad. ABCD)
Hence, area of || gm PQRS = 2.area of quad. ABCD. (Q.E.D.)

Question P.Q.
In the adjoining figure, ABCD and ABEF are parallelogram and P is any point on DC. If area of || gm ABCD = 90 cm², find:
(i) area of || gm ABEF
(ii) area of ∆ABP.
(iii) area of ∆BEF.

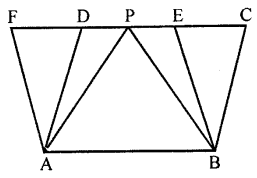
Answer:
In the given figure,
ABCD and ABEF are parallelogram P is an point on DC
Area of ||gm ABCD = 90 cm²
||gm ABCD and ABEF are on the same base AB are between the same parallels
(i) ∴ Area of ||gm ABEF = area of ||gm ABCD = 90 cm²
(ii) ∵ ∆ABP and ||gm ABCD are on the same base AB and between the same parallels
∴ Area ∆ABP = \(\frac{1}{2}\) area ||gm ABCD
= \(\frac{1}{2}\) × 90 cm² = 45 cm²
(iii) ∵∆BEF and ||gm ABEF are on the same base EF and between the same parallels
∵ Area ∆BEF = \(\frac{1}{2}\) area ||gm ABEF
= \(\frac{1}{2}\) × 90 = 45 cm²

Question 2.
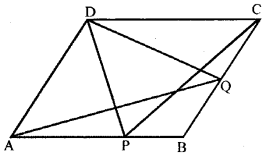
In the parallelogram ABCD, P is a point on the side AB and Q is a point on the side BC. Prove that
(i) area of ∆CPD = area of ∆AQD
(ii)area of ∆ADQ = area of ∆APD + area of ∆CPB.

Answer:
Given. || gm ABCD in which P is a point on AB and Q is a point on BC.
To prove. (i) ar (∆ CPD) = ar ( ∆ AQD)
(ii) ar (∆ ADQ) = ar ( ∆ APD) + ar (∆ CPB)
Proof. ∆ CPD and II gm ABCD are on the same base CD and between the same parallels lines AB and CD.
∴ ar (∆ CPD) = \(\frac{1}{2}\) ar (|| gm ABCD) …..(1)
∆ ADQ and || gm ABCD are on the same base AD and between the same II lines AD and BC,
ar ( ∆ ADQ) = \(\frac{1}{2}\) (|| gm ABCD) ………(2)
From (1) and (2),
ar ( ∆ CPD) = ar( ∆ ADQ)
or ar ( ∆ CPD) = ar (∆ ADQ) (Q.E.D.)

(ii) ar (∆ ADQ) = \(\frac{1}{2}\)ar (|| gm ABCD) ( Proved in part (i) above )
⇒ 2ar (∆ ADQ) = ar (|| gm ABCD)
⇒ ar (∆ ADQ) + ar( ∆ ADQ) = ar (|| gm ABCD) ……..(3)
But ar ( ∆ ADQ) = ar (∆ CPD) …………(4)
(Proved in part (i) above)
From (3) and (4),
ar ( ∆ ADQ) + ar ( ∆ CPD) = ar (|| gm ABCD)
⇒ ar ( ∆ ADQ) + ar ( ∆ CPD)
⇒ ar (∆ APD) + ar (∆ CPD) + ar (∆ CPB)
⇒ or (∆ ADQ) = ar( ∆ APD) + ar (∆ CPB) (Q.E.D.)

Question 3.
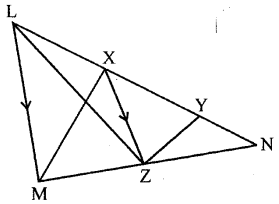
In the adjoining figure, X and Y are points on the side LN of triangle LMN. Through X, a line is drawn parallel to LM to meet MN at Z. Prove that area of ∆LZY = area of quad. MZYX.

Answer:
Given : In the figure,
X and Y are points on side LN of ALMN. Through X, a line XZ || LM is drawn which meets MN at Z.
To prove : area of ∆LZY = area of quad. MZYX
Construction : Join MX, ZY and LZ
Proof: ∆ LM || XZ
and ∆LZX and ∆MZX are on the same base XZ and between the same parallels
∴ area ∆LZX = area ∆MZX
Adding area ∆XZY to both sides area ∆LZX + area ∆XZY
= area ∆MZX + area ∆XZY
⇒ area ∆LZY = area quadrilateral MZYX

Question P.Q.
If D is a point on the base BC of a triangle ABC such that 2BD = DC, prove that area of ∆ABD= \(\frac{1}{2}\) area of ∆ ABC.
Answer:
Given. ∆ ABC in which base BC. D is a point on BC such that 2BD = DC.
To prove, ar ( ∆ ABD) = \(\frac{1}{3}\) ar (ABC)

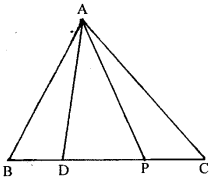
Construction. Let P is the mid-point of DC join AD = DC
⇒ BD = \(\frac{1}{2}\)DC ²
i.e. BD = DP (P is mid-point of DC)
∴ D is mid-point of BP.
In ∆ ABP, AD is median of BP (D is mid-point of BP)
∴ ar (∆ABD) = ar ( ∆ ADP) …..(1)
Again in ∆ ADC, AP is the median of DC. (P is mid-point of DC)
ar (∆ ADP) = ar (∆ APC) ……………(2)
From (1) and (2),
∴ ar (∆ ABD) = ar (∆ ADP) = ar ( ∆ APC)
∴ ∆ ABC is divided into three equal triangles and each A will be of \(\frac{1}{3}\) ∆ ABC.
∴ ar (∆ ABD) = \(\frac{1}{3}\)ar (∆ ABC) (Q.E.D.)

Question 4.
Perpendiculars are drawn from a point within an equilateral triangle to the three sides. Prove that the sum of the three perpendiculars is equal to the altitude of the triangle.
Answer:
ABC is an equilateral triangle, i.e. AB = BC = CA. P is any point within an equilateral triangle to the three sides.

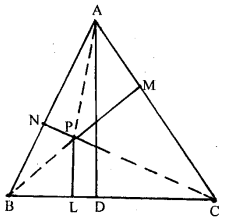
PN, PM, and PL are perpendicular on side AB, AC and BC respectively. AD is any altitude from point A on side BC.
To prove. AD = NP + LP + MP
Construction. Join PA, PB and PC.
Proof. Area of ∆ ABC = \(\frac{1}{2}\) × Base × Altitude
or(∆ABC)= \(\frac{1}{2}\) × BC × AD ………(1)
Now, area of ∆ APB = \(\frac{1}{2}\) × AB × NP ………….(2)
area of ∆ APC = \(\frac{1}{2}\) × AC × MP
area of ∆ BPC = \(\frac{1}{2}\) × BC × LP …….(4)
Adding (2), (3) and (4)
ar ( ∆ APB) + ar (∆ APC) + ar (∆ BPC)
= \(\frac{1}{2}\) × AB × NP + \(\frac{1}{2}\) × AC × MP + \(\frac{1}{2}\) × BC × LP
ar(∆ ABC) = \(\frac{1}{2}\) [AB × NP + AC × MP × BC × LP]
= \(\frac{1}{2}\) [BC × NP + BC MP × BC × LP] (∵ Ab = AC = CA)
ar(∆ABC) = \(\frac{1}{2}\) × BC[NP + MP + LP ] ..(5)
From (4) and (5),
\(\frac{1}{2}\) × BC × AD = \(\frac{1}{2}\) × BC × (NP + LP + MP)
⇒ AD = NP + LP + MP
⇒ NP + LP + MP = AD
i.e.sum of three perpendiculars is equal to the altitude of the triangle.

Question 5.
If each diagonal of a quadrilateral’ divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.
Answer:
Given : In quadrilateral ABCD, diagonal AC bisects the quadrilateral ABCD in two triangle of equal area i.e.

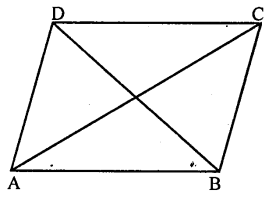
ar (∆ ABC) = ar (∆ ADC)
To prove : ABCD is a parallelogram.
Proof : Join BD.
Proof: ∵ Diagonals of quad. ABCD divides the quad, into two triangles of equal area.
∴ ar( ∆ ABC) = ar( ∆ ABD)
= \(\frac{1}{2}\) ar (ABCD)
But, these are on the same base AB
∴ Their heights are equal
∴ DC || AB …(i)
Similarly, we can prove that :
ar (∆ABC) = ar (∆BDC)
∴ BC || AD …(ii)
From (i) and (ii)
ABCD is a parallelogram.
Hence proved.

Question 6.
In the given figure, ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. If area of ∆DFB = 3 cm², find the area of parallelogram ABCD.

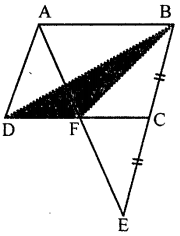
Solution:
In the figure, ABCD is a parallelogram BC is produced to E such that CE = BC

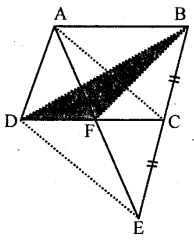
Join BD and AE
which intersects DC at F
Join BF, AC and DE
∴ Area of ∆DFB = 3 cm²
Find the area of ||gm ABCD
Solution:
∵ In ∆ABE, C is mid-point of BE and CD || AB
∴ F is mid-point of AE and CD
∴ ABED is a ||gm (∵ Diagonals AE and CD bisect each other at F)
∵ BD is the diagonal of ||gm ABCD
∆BCD = \(\frac{1}{2}\) ||gm ABCD
∵ F is mid-point of DC
∴ ADFB = \(\frac{1}{2}\) ∆BCD
⇒ ADFB = \(\frac{1}{2}\) × \(\frac{1}{2}\) (||gm ABCD)
⇒ ADFB = \(\frac{1}{2}\) (||gm ABCD)
∴ area ||gm ABCD = 4 area ∆DFB
= 4 × 3 = 12 cm²

Question 7.
In the given figure, ABCD is a square. E and F are mid-points of sides BC and CD respectively. If R is mid-point of EF, prove that: area of ∆AER = area of ∆AFR.

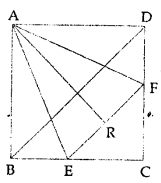
Solution:
Given : In square ABCD, BD is diagonals E and F are mid-point of BC and CD respectively. R is mid-point of EF.
To prove : area (∆AER = area (∆AFR)
Proof: In ∆ABE and ∆ADF
AB = AD (Sides of a square)
∠B = ∠D (Each 90°)
BE = CE (E is mid-point of BC)
∴ ∆ABE ≅ ∆ADF (SAS axiom)
∴ AE = AF (c.p.c.t.)
Again in ∆AER and ∆AFR
AE = AF (Produced)
AR = AR (Common)
ER = FR (R is mid-point of EF)
∴ ∆AER = ∆AFR (SSS axiom)
∴ area(∆AER) = area (∆AFR)

Question 8.
In the given figure, X and Y are mid-points of the sides AC and AB respectively of ∆ABC. QP || BC and CYQ and BXP are straight lines. Prove that area of ∆ABP = area of ∆ACQ.

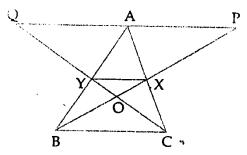
Solution:
Given : In the given figure,
X and Y are the mid-points of the sides AC and AB respectively of ∆ABC
QP || BC
CYQ and BXP are straight lines
To prove : area(∆ABP) = area(∆ACQ)
Proof: v X and Y are the mid-points of sides AC and AB respectively
∴ YX || BC
But QP || BC
∴ QP || BC || YX
In ∆BAP, Y is mid of AB and YX || QP
∴ X is mid-point of BP
∴YX = \(\frac{1}{2}\)AP …(i)
Similarly we can prove in ∆AQC
YX = \(\frac{1}{2}\) QA …(ii)
From (i) and (ii),
QA = AP
Now ∆ABP and ∆ACQ are on the equal base and between the same parallel lines
area(∆ABP) = area(∆ACQ)

ML Aggarwal Class 9 Solutions for ICSE Maths