ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 15 Circle Check Your Progress
Question 1.
Draw a circle of radius 2·7 cm. Draw a chord PQ of length 4 cm of this circle. Shade the major segment of this circle.
Solution:
(i) Draw a circle of radius = 2·7 cm.
(ii) Take a point P anywhere on the circle.
(iii) With P as centre and 4 cm as radius,
draw an arc which cuts the circle at Q.
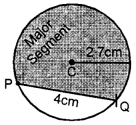
(iv) Join PQ which is the required chord.
(v) Shade the major segment.
Question 2.
Draw a circle of radius 3·2 cm and in it make a sector of angle.
(i) 30°
(ii) 135°
(iii) \(2 \frac{2}{3}\) right angles
Draw separate diagrams and shade the sectors.
Solution:
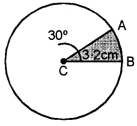
(i) 30°
Steps :
(a) Draw a circle with centre C and radius CB = 3.2 cm
(b) From C, make an angle of 30°.
(c) Shade the region enclosed in ABC.
(ii) 135°
Steps :
(a) Draw a circle with centre C and radius CB = 3.2 cm.
(b) From C, make an angle of 135°.
(c) Shade the region enclosed in ACB.

(iii) \(2 \frac{2}{3}\) right angles
Steps :
(a) Draw a circle with centre C and radius 3.2 cm.
(b) From C, make an ∠, \(2 \frac{2}{3}\) of right angle
= \(2 \frac{2}{3}\) × 90°
= \(\frac{8}{3}\) × 90° = 240°
(c) Shade the region enclosed in ACB.
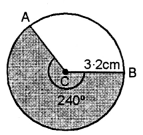
= \(\frac{8}{3}\) × 90° = 240°
Question 3.
Draw a line segment PQ = 6·4 cm. Construct a circle on PQ as diameter. Take any point R on this circle and measure ∠PRQ.
Solution:
(i) Draw a line segment PQ = 6·4 cm.
(ii) Draw ⊥ bisector of PQ.
(iii) With O as centre and OP or OQ as radius draw a circle
which passes through P as well as through Q.
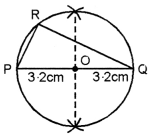
(iv) Take point R on the circle.
(v) Join PR and QR.
(vi) Measure ∠PRQ, we get ∠PRQ = 90°.
Question 4.
In the adjoining figure, the tangent to a circle of radius 6 cm from an external point P is of length 8 cm. Calculate the distance of the point P from the nearest point of the circumference.
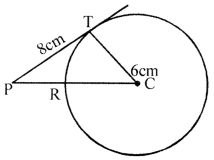
Solution:
C is the centre of the circle
PT is the tangent to the circle from P.
CT is the radius
∴ CT ⊥ PT
CT = CR = 6 cm, PT = 8 cm
Now in right ∆CPT (By Pythagoras Theorem)
CP2 = PT2 + CT2 = (8)2 + (6)2
= 64 + 36 = 100 = (10)2
∴ CP = 10 cm
Now PR = CP – CR = 10 – 6 = 4 cm
Question 5.
In the given figure, O is the centre of the circle. If ∠ABP = 35° and ∠BAQ = 65°, find
(i) ∠PAB
(ii) ∠QBA
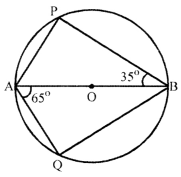
Solution:
In the figure,
AB is the diameter of the circle with centre O
∠ABP = 35° and ∠BAQ = 65°
(i) ∠APB = 90° (Angle in a semicircle)
In ∆APB, By ∠sum property of ∆
∠PAB + ∠P + ∠ABP = 180°
∠PAB + 90° + ∠ABP = 180°
∴ ∠PAB + ∠ABP = 90°
⇒ ∠PAB + 35° = 90° ⇒ ∠PAB = 90° – 35° ∠PAB = 55°
(ii) Similarly ∠AQB = 90° (Angle in a semicircle)
In ∆AOB, By angle sum property of ∆
∠BAQ + ∠Q + ∠QBA = 180°
∠BAQ + ∠QBA + 90° = 180°
∴ ∠BAQ + ∠QBA = 90°
⇒ 65° + ∠QBA = 90°
⇒ ∠QBA = 90°- 65° = 25°
Hence ∠PAB = 55° and ∠QBA = 25°