ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Objective Type Questions

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) A symbol which has a fixed value is called a ……….
(ii) A symbol which can be given various numerical values is called ……….. or ………
(iii) The various parts of an algebraic expression separated by + or – sign are called ………..
(iv) An algebraic expression having ………… terms is called a binomial.
(v) Each of the quantity (constant or literal) multiplied together to form a product is called a ………… of the product.
(vi) The terms having same literal coefficients are called a ………… otherwise they are called …………
(vii) Degree of the polynomial is the greatest sum of the powers of ………… in each term.
(viii)An identity is an equality which is true for ………… of variables in it.
(ix) (a + b)² = …………
(x) (x + a) (x + b) = x² + ………… + ab.
(xi) Dividend = ………… + remainder.
Solution:
(i) A symbol which has a fixed value is called a constant.
(ii) A symbol which can be given various numerical values
is called variable or literal.
(iii) The various parts of an algebraic expression
separated by + or – sign are called terms.
(iv) An algebraic expression having two terms is called a binomial.
(v) Each of the quantity (constant or literal) multiplied together
to form a product is called a factor of the product.
(vi) The terms having same literal coefficients are called
alike terms otherwise they are called unlike terms.
(vii) Degree of the polynomial is the greatest sum of the
powers of variables in each term.
(viii)An identity is an equality which is true
for all values of variables in it.
(ix) (a + b)² = a² + 2ab + b².
(x) (x + a) (x + b) = x² + (a + b)x + ab.
(xi) Dividend = divisor × quotient + remainder.

Question 2.
State whether the following statements are true (T) or false (F):
(i) An algebraic expression having only one term is called a monomial.
(ii) A symbol which has fixed value is called a literal.
(iii) The term of an algebraic expression having no literal factor is called its constant term,
(iv) In any term of an algebraic expression the constant part is called literal coefficient of the term.
(v) An algebraic expression is called polynomial if the powers of the variables involved in it in each term are non-negative integers.
(vi) 5x²y²z, 3x²zy², – \(\frac{4}{5}\) zx²y² are unlike terms.
(vii) 5x + \(\frac{2}{x}\) + 7 is a polynomial of degree 1.
(viii) 3x²y + 7x + 8y + 9 is a polynomial of degree 3.
(ix) Numerical coefficient of -7x³y is 7.
(x) An equation is true for all values of variables in it.
(xi) (a – b)² + 2ab = a² + b².
Solution:
(i) An algebraic expression having only one term is called a monomial. True
(ii) A symbol which has fixed value is called a literal. False
Correct:
It is called constant.
(iii) The term of an algebraic expression having
no literal factor is called its constant term.
True
(iv) In any term of an algebraic expression, the constant part
is called literal coefficient of the term. False
Correct:
It is called the constant coefficient.
(v) An algebraic expression is called polynomial if the powers
of the variables involved in it in each term are non-negative integers. True
(vi) 5x²y²z, 3x²zy², – \(\frac{4}{5}\) zx²y² are unlike terms.
False
Correct:
They are like terms.
(vii) 5x + \(\frac{2}{x}\) + 7 is a polynomial of degree 1. False
Correct:
∵ \(\frac{2}{x}\) has negative power of y i.e. x^-1.
(viii)3x²y + 7x + 8y + 9 is a polynomial of degree 3. True
(ix) Numerical coefficient of -7x³y is 7. False Correct:
It is -7.
(x) An equation is true for all values of variables in it. False
Correct:
It is true for some specific values of variables.
(xi) (a – b)² + 2ab = a² + b². True

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 18):
Question 3.
The literal coefficient of -9xyz² is
(a) -9
(b) xy
(c) xyz²
(d) -9xy
Solution:
Literal co-efficient of -9xyz² is -9 (a)

Question 4.
Which of the following algebraic expression is
(a) 3x² – 2x + 7
(b) \(\frac{5 x^{3}}{2 x}\) + 3x² + 8
(c) 3x + \(\frac{2}{x}\) + 7
(d) \(\sqrt{2}\)x² + \(\sqrt{3}\)x + \(\sqrt{6}\)
Solution:
3x² – 2x + 7 is not an algebraic expression. (c)

Question 5.
Which of the following algebraic expressions is not a monomial?
(a) 3x × y × z
(b) -5pq
(c) 8m² × n ÷ 31
(d) 7x ÷ y – z
Solution:
7x ÷ y – z = \(\frac{7 x}{y}\) – z
It is not monomial.
(As it has two terms) (d)

Question 6.
Degree of the polynomial 7x²yz² + 6x³y²z² – 5x + 8y is
(a) 4
(b) 5
(c) 6
(d) 7
Solution:
Degree of polynomial
7x²yz² + 6x³y²z² -5x + 8y is 3 + 2 + 2 = 7 (d)

Question 7.
a(b -c) + b(c – a) + c(a – b) is equal to
(a) ab + bc + ca
(b) 0
(c) 2(ab + bc + ca)
(d) none of these
Solution:
a(b -c) + b(c – a) + c(a – b)
= ab – ac + bc – ab + ac – bc = 0 (b)

Question 8.
\(\frac{7}{5}\)xy – \(\frac{2}{3}\)xy + \(\frac{8}{9}\) xy is equal to

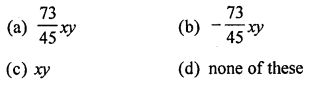
Solution:
\(\frac{7}{5}\)xy – \(\frac{2}{3}\)xy + \(\frac{8}{9}\) xy
= \(\frac{63 x y-30 x y+40 x y}{45}=\frac{73}{45} x y\) (a)

Question 9.
(3p²qr³) × (-4p³q²r²) x (7pq³r) is equal to
(a) 84p⁶q⁶r⁶
(b) -84p⁶q⁶r⁶
(c) 84p⁶q⁵r⁶
(d) -84p⁶q⁵r⁶
Solution:
(3p²qr³) × (-4p³q²r²) × (7pq³r)
= 3(-4) × 7p²⁺³⁺¹ × q¹⁺²⁺³ × r³⁺²⁺¹
= -84p⁶q⁶r⁶ (b)

Question 10.
3m × (2m² – 5mn + 4n²) is equal to
(a) 6m³ + 15m²n – 12mn²
(b) 6m³ – 15m²n + 12mn²
(c) 6m³ – 15m²n – 12mn²
(d) 6m³ + 15m²n + 12mn²
Solution:
3m × (2m² – 5mn + 4n²)
= 6m³ – 15m²n + 12mn² (b)

Question 11.
Volume of a rectangular box whose adjacent edges are 3x²y, 4y²z and 5z²x respectively is
(a) 60xyz
(b) 60x²y²z²
(c) 60x³y³z³
(d) none of these
Solution:
Volume = 3x²y × 4y²z × 5z²x = 60x³y³²z³ (c)

Question 12.
(x – 1) (x + 2) is equal to
(a) 2x + 3
(b) x² + 2x + 2
(c) x² + 3x + 2
(d) x² + 2x + 3
Solution:
(x + 1) (x + 2) = x² + (1 + 2)x + 1 × 2
= x² + 3x + 2 (c)

Question 13.
If x + \(\frac{1}{x}\) = 2, then x² + \(\frac{1}{x^{2}}\) is equal to
(a) 4
(b) 2
(c) 0
(d) none of these
Solution:
x + \(\frac{1}{x}\) = 2
Squaring both sides,

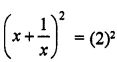
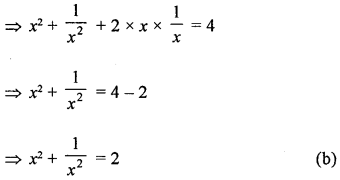
Question 14.
If x² + y² = 9 and xy = 8, then x + y is equal to
(a) 25
(b) 5
(c) -5
(d) ±5
Solution:
x² + y² = 9, xy = 8
(x + y)² = x² + y² + 2xy
= (9)² + 2 × 8
= 9 + 16 = 25 = ±(5) (d)

Question 15.
(102)² – (98)² is equal to
(a) 200
(b) 400
(c) 600
(d) 800
Solution:
(102)² – (98)²
= (102 + 98) × (102 – 98)
= 200 × 4 = 800 (d)

Question 16.
-50x³y²z² divided by -5xyz is equal to
(a) 10xyz
(b) 10x²yz
(c) -10xyz
(d) -10x²yz
Solution:
\(\frac{-50 x^{3} y^{2} z^{2}}{-5 x y z}\) = 10x²yz (b)

Question 17.
96 × 104 is equal to
(a) 9984
(b) 9974
(c) 9964
(d) none of these
Solution:
96 × 104 = (100 – 4) (100 + 4)
= (100)² – (4)²
= 10000 – 16 = 9984 (a)

Question 18.
If the area of a rectangle is 24(x²yz + xy²z + xyz²) and its length is 8xyz, then its breadth is
(a) 3(x + y + z)
(b) 3xyz
(c) 3(x + y – z)
(d) none of these
Solution:
In a rectangle
Area = 24(x²yz + xy²z + xyz²)
Length = 8xyz
Breadth = \(\frac{24 x y z(x+y+z)}{8 x y z}\) = 3(x + y + z) (a)

Higher Order Thinking Skills (Hots)
Question 1.
Using the identity (a + b) = a² + 2ab + b², derive the formula for (a + b + c)². Hence, find the value of (2x – 3y + 4z)².
Solution:
(a + b)² = a² + 2ab + b²
(a + b + c)² = (a + b)² + c² + 2 (a + b)c
= a² + b² + 2ab + c² + 2ca + 2bc
= a² + b² + c² + 2ab + 2bc + 2ca
(2x – 3y + 4z)² = (2x)² + (3y)² + (4z)² + 2 × 2x × (-3y)
+ 2(-3y) (4z) + 2(4z) (2x)
= 4x² + 9y² + 16z² – 12xy – 24yz + 16zx

Question 2.
Using the product of algebraic expressions, find the formulas for (a + b)² and (a – b).
Solution:
(a + b)² = (a + b)² (a + b)
= (a² + 2ab + b²) (a + b)
= a(a² + 2ab + b²) + b(a² + 2ab + b²)
= a³ + 2a²b + ab² + a²b + 2ab² + b³
= a³² + b³ + 3a²b + 3ab²
= a² + b2² + 3ab(a + b)

(a – b)² = (a – b) (a – b)²
= (a – b) (a² – 2ab + b²)
= a(a² – 2ab + b²) – b(a² – 2ab + b²)
= a³ – 2a²b + ab² – a²b + 2ab² – b³
= a³ – b³ – 3a²b + 3ab²
= a³ – b³ – 3ab(a – b)

ML Aggarwal Class 8 Solutions for ICSE Maths