ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 1 Rational Numbers Ex 1.5
Question 1.
Represent the following rational numbers on the number line:
(i) \(\frac { 11 }{ 4 }\)
(ii) 4\(\frac { 3 }{ 5 }\)
(iii) \(\frac { -9 }{ 7 }\)
(iv) \(\frac { -2 }{ -5 }\)
Solution:
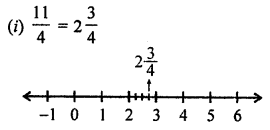
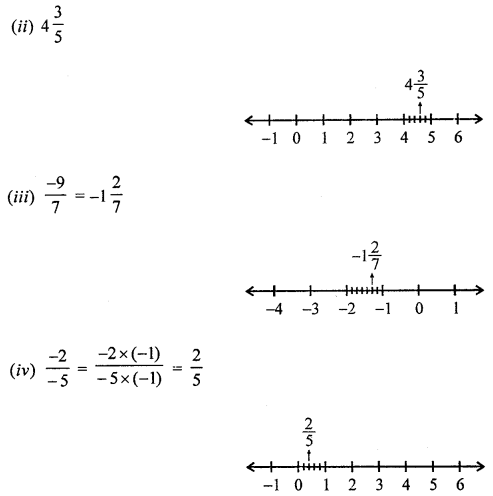
Question 2.
Write the rational numbers for each point labelled with a letter:
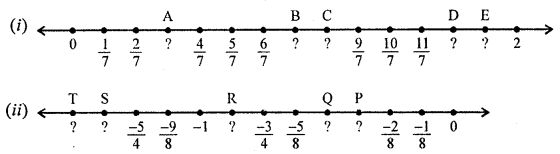
Solution:
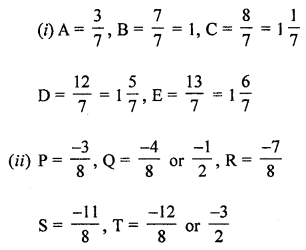
Question 3.
Find twenty rational numbers between \(\frac { -3 }{ 7 }\) and \(\frac { 2 }{ 3 }\)
Solution:
20 rational numbers between \(\frac { -3 }{ 7 }\) and \(\frac { 2 }{ 3 }\)
LCM of 7, 3 = 21

Question 4.
Find six rational numbers between \(\frac { -1 }{ 2 }\) and \(\frac { 5 }{ 4 }\)
Solution:
6 rational numbers between \(\frac { -1 }{ 2 }\) and \(\frac { 5 }{ 4 }\)
LCM of 2, 4 = 4
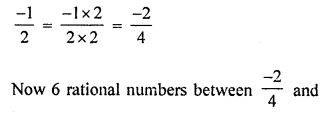
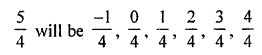
Question 5.
Find three rational numbers between -2 and -1.
Solution:
3 rational numbers between -2 and -1
First rational number = \(\frac { 1 }{ 2 }\) (-1 – 2) = \(\frac { -3 }{ 2 }\)
Second rational number between -2 and \(\frac { -3 }{ 2 }\)
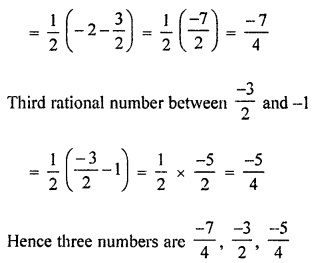
Question 6.
Write ten rational numbers which are greater than 0.
Solution:
Ten rational numbers which are greater than 0.
There can be the infinite number of a rational number greater than 1.
We shall take only 10 to rational numbers such as
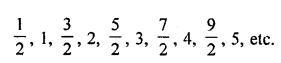
Question 7.
Write five rational numbers which are smaller than -4.
Solution:
5 rational numbers which are smaller than -4.
These can be infinite numbers of rational numbers smaller than -4.
We shall take only 5 rational numbers such as
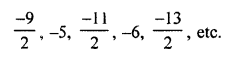
Question 8.
Identify the rational number which is different from the other three. Explain your reasoning
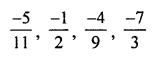
Solution:
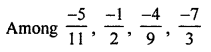
\(\frac { -7 }{ 3 }\) is different as its denominator is less than its numerator,
in others, denominators are greater than their numerators respectively.