ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 9 Linear Equations and Inequalities Ex 9.2
Question 1.
If 7 is added to five times a number, the result is 57. Find the number.
Solution:
Let the number be x
Five times a number is = 5x
If 7 is added, it becomes 7 + 5x
According to given condition,
7 + 5x = 57
⇒ 5x = 57 – 7
⇒ 5x = 50
⇒ x = 10
Question 2.
Find a number, such that one-fourth of the number is 3 more than 7.
Solution:
Let number = x
According to the condition,
\(\frac { 1 }{ 4 }\) x – 3 = 7
\(\frac { 1 }{ 4 }\) x = 7 + 3 = 10
x = 10 × 4 = 40
Number = 40
Question 3.
A number is as much greater than 15 as it is less than 51. Find the number.
Solution:
Let the number be x
If it is greater than 15, it becomes x – 15.
If it is less than 51, it becomes 51 – x
According to statement,
x – 15 = 51 – x
⇒ x + x = 51 + 15
⇒ 2x = 66
⇒ x = 33
Question 4.
If \(\frac { 1 }{ 2 }\) is subtracted from a number and the difference is multiplied by 4, the result is 5. What is the number?
Solution:
Let the number = x
According to the condition,
(x – \(\frac { 1 }{ 2 }\)) × 4 = 5
⇒ 4x – 2 = 5
⇒ 4x = 5 + 2
⇒ 4x = 7
⇒ x = \(\frac { 7 }{ 4 }\)
Number = \(\frac { 7 }{ 4 }\)
Question 5.
The sum of two numbers is 80 and the greater number exceeds twice the smaller by 11. Find the numbers.
Solution:
Let the numbers be x and y
Smaller number = x
Greater number = y
If greater number exceeds twice the smaller by 11,
It becomes y = 2x + 11
According to statement,
x + 2x + 11 = 80
⇒ 3x + 11 = 80
⇒ 3x = 80 – 11
⇒ 3x = 69
⇒ x = 23
Smaller number = 23
Greater number = 2x + 11 = 2 × 23 + 11 = 46 + 11 = 57
Question 6.
Find three consecutive odd natural numbers whose sum is 87.
Solution:
Let the three consecutive odd natural numbers be
x, x + 2, x + 4.
According to statement,
x + x + 2 + x + 4 = 87
⇒ 3x + 6 = 87
⇒ 3x = 81
⇒ x = 27
x + 2 = 27 + 2 = 29 and x + 4 = 27 + 4 = 31
Three consecutive odd natural numbers are 27, 29 and 31.
Question 7.
In a class of 35 students, the number of girls is two-fifths of the number of boys. Find the number of girls in the class.
Solution:
Let the number of boys = x
The number of girls = \(\frac { 2x }{ 5 }\)
According to statement,
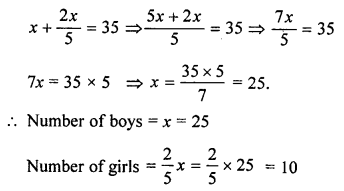
Question 8.
A chair costs ₹ 250 and the table costs ₹ 400. If a housewife purchased a certain number of chairs and two tables for ₹ 2800, find the number of chairs she purchased.
Solution:
Cost of a chair = ₹ 250
and cost of a table = ₹ 400
Let number of chairs = x
and number of tables = 2
Total cost = ₹ 2800
x × 250 + 2 × 400 = 2800
⇒ 250x + 800 = 2800
⇒ 250 x = ₹ 2800 – ₹ 800 = ₹ 2000
⇒ x = 8
Number of chairs = 8
Question 9.
Aparna got ₹ 27840 as her monthly salary and over-time. Her salary exceeds the overtime by ₹ 16560. What is her monthly salary?
Solution:
Let Apama’s monthly salary = ₹ x
Then over-time payment = ₹ (27840 – x)
According to the condition,
x – (27840 – x) = 16560
⇒ x – 27840 + x = 16560
⇒ 2x = 16560 + 27840 = ₹ 44400
⇒ x = 22200
Monthly salary = ₹ 22200
Question 10.
Heena has only ₹ 2 and ₹ 5 coins in her purse. If in all she has 80 coins in her purse amounting to ₹ 232, find the number of ₹ 5 coins.
Solution:
Total number of coins = 80
Let the number of ₹ 2 coins = x
The number of ₹ 5 coins = 80 – x
According to given statement,
2x + 5 (80 – x) = 232
⇒ 2x + 400 – 5x = 232
⇒ -3x = 232 – 400
⇒ -3x = -168
⇒ x = 56
Number of ₹ 5 coins = 80 – x = 80 – 56 = 24
Number of ₹ 5 coins = 24
Question 11.
A purse contains ₹ 550 in notes of denominations of ₹ 10 and ₹ 50. If the number of ₹ 50 notes is one less than that of ₹ 10 notes, then find the number of ₹ 50 notes.
Solution:
Total amount in a purse = ₹ 550
Let number of notes of ₹ 10 = x
The number of notes of ₹ 50 = x – 1
According to the condition,
x × 10 + (x – 1) × 50 = 550
⇒ 10x + 50x – 50 = 550
⇒ 10x = 550 + 50 = 600
⇒ x = 10
50 rupees notes = 10 – 1 = 9
Question 12.
After 12 years, 1 shall be 3 times as old as I was 4 years ago. Find my present age.
Solution:
Let my present age = x years
After 12 years, I will be = (x + 12) years
and 4 years ago, I was = (x – 4) years
According to the condition,
(x – 4) × 3 = x + 12
⇒ 3x – 12 = x + 12
⇒ 3x – x = 12 + 12
⇒ 2x = 24
⇒ x = 12
My present age = 12 years
Question 13.
Two equal sides of an isosceles triangle are 3x – 1 and 2x + 2. The third side is 2x units. Find x and the perimeter of the triangle.
Solution:
Two equal sides of an isosceles Δ are 3x – 1 and 2x + 2
3x – 1 = 2x + 2
3x – 2x = 2 + 1
x = 3
We know that
Perimeter of a Δ = (3x – 1) + (2x + 2) + (2x)
= (3 × 3 – 1) + (2 × 3 + 2) + (2 × 3)
= (9 – 1) + (6 + 2) + (6)
= 8 + 8 + 6
= 22 units
Question 14.
The length of a rectangle plot is 6 m less than thrice its breadth. Find the dimensions of the plot if its perimeter is 148 m.
Solution:
Let the breadth of a rectangle = x m.
Thrice its breadth = 3x m
Length of a rectangle = 3x – 6 m
Perimeter of a rectangle = 2 (l + b)
= 2 (3x – 6 + x)
= 2 (4x – 6)
= 8x – 12
But we are given, perimeter = 148 m
8x – 12= 148
8x = 148 + 12
8x = 160
x = 20 metres
Breadth = x = 20 metres
and Length = 3x – 6 = 3 × 20 – 6 = 60 – 6 = 54 metres.
Question 15.
Two complementary angles differ by 20°. Find the measure of each angle.
Solution:
We know that
Sum of measures of two complementary angles = 90°
⇒ x + y = 90° ……. (i)
But we are given x – y = 20° …… (ii)
2x = 110° [On comparing (i) and (ii)]
⇒ x = 55°
Now, x + y = 90°
⇒ y = 90° – x
⇒ y = 90° – 55° = 35°