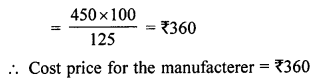ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 7 Percentage and Its applications Objective Type Questions
Question 1.
Fill in the blanks:
(i) 6% of ₹ 50 = ……….
(ii) If 25% of a number is 12, then the number is ……….
(iii) The mixed fraction 1\(\frac { 3 }{ 4 }\) converted to percentage form is
(iv) If a number increases from 20 to 28, then the increasing percentage is ………
(v) If cost price is ₹ 400 and loss is 15%, then the selling price is ……..
(vi) The profit or loss percentage is always calculated on ……….
(vii) The simple interest on a sum of ₹ 5600 at 8% p.a. for one year is ……….
(viii) 135% converted to decimal is ………
(ix) ……… is 50% more than 60.
(x) 25 mL is ………… percent of 5 litres.
Solution:
(i) 6% of ₹ 50 = \(\frac { 50\times 6 }{ 100 }\) = ₹ 3.
(ii) If 25% of a number is 12, then the number is …….
25% of a number = 12
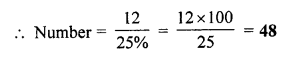
(iii) The mixed fraction 1\(\frac { 3 }{ 4 }\) converted into percentage form is ………
1\(\frac { 3 }{ 4 }\) = \(\frac { 7 }{ 4 }\)
= \(\frac { 7\times 100 }{ 4 }\)
= 175 %
(iv) If a number increases from 20 to 28, then the increase percentage is …….
A number is increases from 20 to 28
Increase = 28 – 20 = 8
Increase% = \(\frac { 8\times 100 }{ 20 }\) = 40%
(v) If cost price is ₹ 400 and loss is 15%, then selling price is …….
C.P. = ₹ 400
Loss = 15%
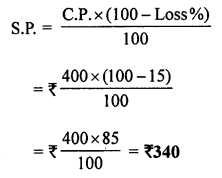
(vi) The profit or loss percentage is always calculated on C.P.
(vii) The simple interest on a sum of ₹ 5600 at 8% p.a. for one year is ……..
S.I. on ₹ 5600 for 1 year at 8 % p.a.
= \(\frac { 5600\times 1\times 8 }{ 100 }\)
= ₹ 448
(viii) 135% converted to decimal is …….
135 % = \(\frac { 135 }{ 100 }\) = 1.35
(ix) …….. is 50% more than 60.
Let required number = x
Then 50% of 60 + 60
= \(\frac { 50 }{ 100 }\) × 60 + 60 = 30 + 60 = 90
90 is 50% more than 60
(x) 25 mL is …….. percent of 5 litres.
25 mL (5 l = 5000mL)
= \(\frac { 25 }{ 5000 }\) × 100
= \(\frac { 1 }{ 2 }\)
= 0.5% of 5 litres
Question 2.
State whether the following statements are true (T) or false (F):
(i) 20% more than 30 is 36.
(ii) The ratio 2 : 5 converted to percentage is 60%.
(iii) 6\(\frac { 1 }{ 4 }\) % expressed as a fraction is \(\frac { 1 }{ 16 }\).
(iv) 80% of 450 m is equal to 360 m.
(v) If a number decreases from 20 to 15, then the decrease is 25%.
(vi) If Feroz obtains 336 marks out of600 marks,
then the percentage of marks obtained by him is 33.6.
(vii) 0.018 is equivalent to 8%.
(viii) 250 cm is 4% of 1 km.
(ix) If S.P. of an article is ₹ 540 and loss is ₹ 40, then its C.P. is ₹ 500.
(x) By selling a book for ₹ 50, a shopkeeper suffers a loss of 10%.
The cost price of the books is ₹ 60.
Solution:
(i) 20% more than 30 is 36. (True)
Required number = \(\frac { 20 }{ 100 }\) × 30 + 30 = 6 + 30 = 36
(ii) The ratio 2 : 5 converted to percentage is 60%. (False)
Correct:
Ratio 2 : 5 = \(\frac { 2 }{ 5 }\) × 100 = 40% not 60%
(iii) 6\(\frac { 1 }{ 4 }\) % expressed as a fraction is \(\frac { 1 }{ 16 }\). (True)
6\(\frac { 1 }{ 4 }\) % or \(\frac { 25 }{ 4 }\) %
= \(\frac { 25 }{ 4\times 100 } =\frac { 1 }{ 16 }\)
(iv) 80% of 450 m is equal to 360 m. (True)
\(\frac { 80 }{ 100 }\) × 450 m = 360
(v) If a number decreases from 20 to 15, then the decrease is 25%. (True)
Total decrease = 20 – 15 = 5
Decrease % = \(\frac { 5\times 100 }{ 20 }\) = 25%
(vi) If Feroz obtains 336 marks out of600 marks,
then percentage of marks obtained by him is 33.6. (False)
Correct:
336 marks out of 600
Percentage of marks = \(\frac { 336\times 100 }{ 600 }\)
= 56% not 33.6
(vii) 0.018 is equivalent to 8%. (False)
Correct:
0.018 = \(\frac { 0.018 }{ 1000 }\) = \(\frac { 18\times 100 }{ 1000 }\)
= 1.8% not 18%
(viii) 250 cm is 4% of 1 km. (False)
Correct:
1 km = 1000 × 100 cm
= 100000 × \(\frac { 4 }{ 100 }\)
= 4000 cm not 250 cm
(ix) If S.P. of an article is ₹ 540 and loss is ₹ 40, then its C.P. is ₹ 500. (False)
Correct:
S.P. of an article = ₹ 540
Loss = ₹ 40
C.P. = ₹ 540 + ₹ 40 = ₹ 580 not ₹ 500
(x) By selling a book for ₹ 50, a shopkeeper suffers a loss of 10%.
The cost price of the books is ₹ 60. (False)
Correct:
S.P. of a book = ₹ 50
Loss = 10%
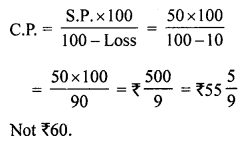
Multiple Choice Questions
Choose the correct answer from the given four options (3 to 16):
Question 3.
The ratio 2 : 3 expressed as percent is
(a) 40%
(b) 60%
(c) 66\(\frac { 2 }{ 3 }\) %
(d) 33\(\frac { 1 }{ 3 }\) %
Solution:
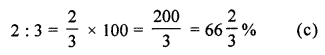
Question 4.
The ratio of Fatima’s income to her saving is 4 : 1. The percentage of money saved by her is
(a) 20%
(b) 25%
(c) 40%
(d) 80%
Solution:
Ratio in income and savings = 4 : 1
Percent saving = \(\frac { 1 }{ 4 }\) × 100 = 25% (b)
Question 5.
225% is equal to
(a) 2 : 3
(b) 3 : 2
(c) 4 : 9
(d) 9 : 4
Solution:
225% = \(\frac { 225 }{ 100 }\) = 9 : 4 (d)
Question 6.
If 30% of x is 72, then x is equal to
(a) 120
(b) 240
(c) 360
(d) 480
Solution:
30% of x = 72
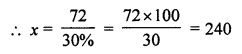
Question 7.
If x% of 80 = 12, then x is equal to
(a) 15
(b) 20
(c) 25
(d) 30
Solution:
x% of 80 = 12
x = \(\frac { 12\times 100 }{ 80 }\) = 15 (a)
Question 8.
0.025 when expressed as a percent is
(a) 250%
(b) 25%
(c) 4%
(d) 2.5%
Solution:
0.025 = \(\frac { 25 }{ 1000 }\) = 2.5% (d)
Question 9.
In a class, 45% of students are girls. If there are 22 boys in the class, then the total number of students in the class is
(a) 30
(b) 36
(c) 40
(d) 44
Solution:
Girls one 45% of students in a class
Boys = 100 – 45 = 55%
55% of students = 22
Number of students = \(\frac { 22\times 100 }{ 55 }\) = 40 (c)
Question 10.
What percent of \(\frac { 1 }{ 7 }\) is \(\frac { 2 }{ 35 }\) ?
(a) 20%
(b) 25%
(c) 30%
(d) 40%
Solution:
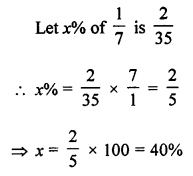
Question 11.
If a man buys an article for ₹ 80 and sells it for ₹ 100, then gain percentage is
(a) 20%
(b) 25%
(c) 40%
(d) 125%
Solution:
C.P. of an article = ₹ 80 and S.P. = ₹ 100
Gain = ₹ 100 – ₹ 80 = ₹ 20
Gain% = \(\frac { 20\times 100 }{ 80 }\) = 25% (b)
Question 12.
If a man buys an article for ₹ 120 and sells it for ₹ 100, then his loss percentage is
(a) 10%
(b) 20%
(c) 25%
(d) 16\(\frac { 2 }{ 3 }\)%
Solution:
C.P. of an article = ₹ 120
and S.P. = ₹ 100
Loss = ₹ 120 – ₹ 100 = ₹ 20
Loss% = \(\frac { 20\times 10 }{ 120 }\)
= \(\frac { 50 }{ 3 }\) %
= 16\(\frac { 2 }{ 3 }\)% (d)
Question 13.
The salary of a man is ₹ 24000 per month. If he gets an increase of 25% in the salary, then the new salary per month is
(a) ₹ 2500
(b) ₹ 28000
(c) ₹ 30000
(d) ₹ 36000
Solution:
Salary of a man = ₹ 24000
Increase = 25%
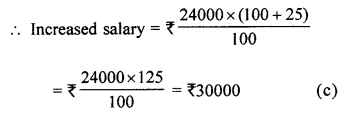
Question 14.
On selling an article for ₹ 100, Renu gains ₹ 20. Her gain percentage is
(a) 25%
(b) 20%
(c) 15%
(d) 40%
Solution:
S.R of an article = ₹ 100
Gain = ₹ 20
C.P. = ₹ 100 – ₹ 20 = ₹ 80
Gain% = \(\frac { 20\times 100 }{ 80 }\) = 25% (a)
Question 15.
The simple interest on ₹ 6000 at 8% p.a. for one year is
(a) ₹ 600
(b) ₹ 480
(c) ₹ 400
(d) ₹ 240
Solution:
S.I. on ₹ 6000 for 1 year at 8% p.a.
= \(\frac { 600\times 1\times 8 }{ 100 }\)
= ₹ 480 (b)
Question 16.
If Rohit borrows ₹ 4800 at 5% p.a. simple interest, then the amount he has to return at the end of 2 years is
(a) ₹ 480
(b) ₹ 5040
(c) ₹ 5280
(d) ₹ 5600
Solution:
Principal (P) = ₹ 4800
Rate (R) = 5%
Time (T) = 2 years
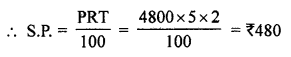
and Amount = P + S.I. = ₹ 4800 + ₹ 480 = ₹ 5280
Value Based Questions
Question 1.
One bad apple is accidently mixed with some good apples in a basket. As a result of which 25% of the total apples go bad. Now the number of good apples in the basket is 30. Find the number of good apples kept in the basket previously. What will happen if one bad person is mixed with some good ones?
Solution:
Bad apples in the basket = 25% the total apples
Good apples = 100 – 25 = 75%
Now 75% of the total apples = 30
Total apples = \(\frac { 30\times 100 }{ 75 }\) = 40
One bad apple which was mixed,
so number of apples in the basket = 40 – 1 = 39
Question 2.
There is a group of 50 people who are patriotic out of which 40% believe in non-violence. Find the number of persons who believe in non-violence. Explain the importance of non-violence in patriotism.
Solution:
Number of people in a group = 50
Number of people who believe non-violence = 40%
Number of people who believe in non-violence = 50 × \(\frac { 40 }{ 100 }\) = 20
In order to keep the environment peace find,
we should believe in non-violence and patriotism with violence
can be dangerous for the common people of the country.
Higher Order Thinking Skills (HOTS)
Question 1.
A person preparing medicine wants to convert 15% alcohol solution into 32% alcohol solution. Find how much pure alcohol should he mix with 400 mL of 15% alcohol solution to obtain it.
Solution:
A person wants to convert 15% alcohol solution into 32% alcohol.
There is 400 mL of 15% solution
Quantity of pure alcohol = 400 – \(\frac { 400\times 15 }{ 100 }\)
= 400 – 60 mL = 340 mL
Now the order to get 32% mixture the quantity of alcohol = 100 – 32 = 68%
Quantity of alcohol = \(\frac { 340\times 100 }{ 68 }\) = 50 mL
New pure alcohol to be aded = 500 – 400 = 100 mL
Question 2.
A manufacturer sells an item to an agency at a profit of 25%. The agency sells the item to a shopkeeper at 10% profit and shopkeeper sells the item at a profit of 20%. If the selling price of the item is ₹ 594, find the manufacturing price.
Solution:
S.P. of an item = ₹ 594
Profit = 20%