ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 7 Percentage and Its applications Ex 7.4
Question 1.
Find the simple interest on:
(i) ₹ 350 for 2 years at 11% per annum
(ii) ₹ 20000 for 4\(\frac { 1 }{ 2 }\) years at 8\(\frac { 1 }{ 2 }\) % per annum
(iii) ₹ 648 for 8 months at 16\(\frac { 2 }{ 3 }\) % per annum. Also, find the amount in each case.
Solution:
(i) Principal (P) = ₹ 350
Rate (R) = 11% p.a.
Time (T) = 2 years
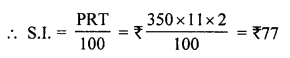
Amount = P + S.I. = ₹ 350 + ₹ 77 = ₹ 427
(ii) Principal (P) = ₹ 20000
Rate (R) = 8\(\frac { 1 }{ 2 }\) = \(\frac { 17 }{ 2 }\) % p.a.
Time (T) = 4\(\frac { 1 }{ 2 }\) years = \(\frac { 9 }{ 2 }\) years
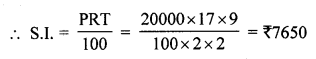
and amount = P + S.I. = ₹ 20000 + ₹ 7650 = ₹ 27650
(iii) Principal (P) = ₹ 648

Amount = P + S.I. = ₹ 648 + ₹ 72 = ₹ 720
Question 2.
Find the time when:
(i) simple interest on ₹ 2500 at 4% per annum is ₹ 200
(ii) simple interest on ₹ 12000 at 6\(\frac { 1 }{ 2 }\) % per annum is ₹ 2730
Solution:
(i) S.I. = ₹ 200
Principal (P) = ₹ 2500
Rate (R) = 4% p.a.
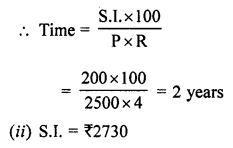
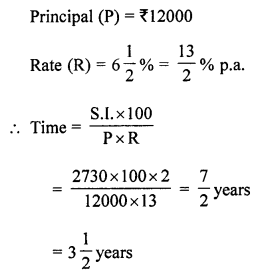
Question 3.
Find the rate of interest when:
(i) simple interest on ₹ 1560 in 3 years is ₹ 585
(ii) simple interest on ₹ 1625 in 2\(\frac { 1 }{ 2 }\) years is ₹ 325.
Solution:
(i) S.I. = ₹ 585
Principal (P) = ₹ 1560
Time (T) = 3 years
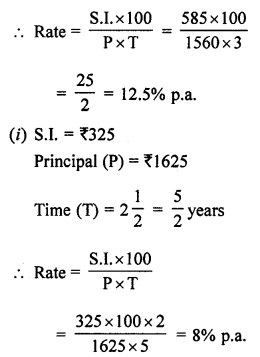
Question 4.
Find the principal when:
(i) simple interest at 16% per annum for 2\(\frac { 1 }{ 2 }\) years is ₹ 3840
(ii) simple interest at 7\(\frac { 1 }{ 2 }\) % per annum for 2 years 4 months is ₹ 2730.
Solution:
(i) S.I. = ₹ 3840
Rate (R) = 16% p.a.
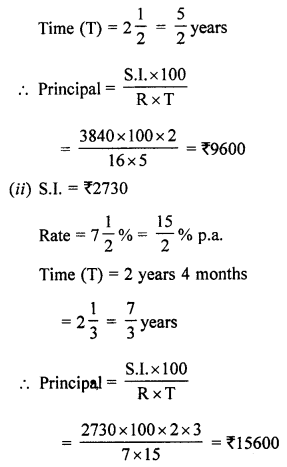
Question 5.
Find the rate of interest when:
(i) ₹ 1200 amounts to ₹ 1320 in 2 years
(ii) ₹ 300 amounts to ₹ 400 in 2 years.
Solution:
(i) Principal (P) = ₹ 1200
Amount (A) = ₹ 1320
S.I. = A – P = ₹ 1320 – ₹ 1200 = ₹ 120
Time (T) = 2 years

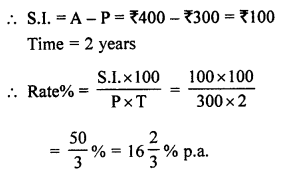
Question 6.
Find the time when:
(i) ₹ 1250 amounts to ₹ 1950 at 16% per annum
(ii) ₹ 6540 amounts to ₹ 8447.50 at 12\(\frac { 1 }{ 2 }\) per annum.
Solution:
(i) Principal (P) = ₹ 1250
Amount (A) = ₹ 1950
S.I. = A – P = ₹ 1950 – ₹ 1250 = ₹ 700
Rate = 16% p.a.
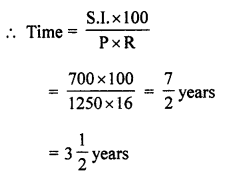
(ii) Principal (P) = ₹ 6540
Amount (A) = ₹ 8447.50
S.I. = A – P = ₹ 8447.50 – 6540.00 = ₹ 1907.50
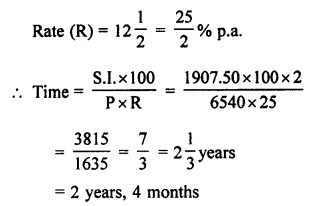
Question 7.
₹ 14000 is invested at 4% per annum simple interest. How long will it take for the amount to reach ₹ 16240?
Solution:
Principal (P) = ₹ 14000
Amount (A) = ₹ 16240
S.I. = A – P = ₹ 16240 – ₹ 14000 = ₹ 2240
Rate (R) = 4%
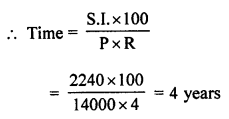
Question 8.
An amount of money invested trebled in 6 years. Find the rate of interest earned.
Solution:
Time (T) = 6 years
Let principal = ₹ 100
Then amount = ₹ 100 × 3 = ₹ 300
S.I. = A – P = ₹ 300 – ₹ 100 = ₹ 200
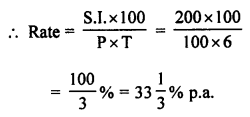
Question 9.
Find the principal when:
(i) final amount is ₹ 4500 at 20% per annum for 5 years
(ii) final amount is ₹ 2420 at 4% per annum for 2\(\frac { 1 }{ 2 }\) years.
Solution:
(i) Amount (A) = ₹ 4500
Rate (R) = 20%
Time (T) = 5 years
Let principal (P) = ₹ 100
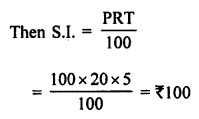
and amount = P + S.I = ₹ 100 + ₹ 100 = ₹ 200
If amount is ₹ 200 then principal = ₹ 100
and if amount is ₹ 4500 then principal
= \(\frac { 100 }{ 200 }\) × 4500
= ₹ 2250
(iii) Amount (A) = ₹ 2420
Rate (R) = 4% p.a.
Time (T) = 2\(\frac { 1 }{ 2 }\) = \(\frac { 5 }{ 2 }\) years
Let principal = ₹ 100
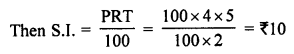
Amount = P + S.I. = ₹ 100 + ₹ 10 = ₹ 110
If amount is ₹ 110 then principal = ₹ 100
If amount is ₹ 2420, then principal
= \(\frac { 100\times 2420 }{ 110 }\)
= ₹ 2200